Introducción al módulo analítico NumPy¶

Configuración previa¶

El análisis de datos básico en Python se realiza utilizando tres bibliotecas que se complementan perfectamente entre ellas:

• NumPy: Para manejar arrays.
• Pandas: Para manejar dataframes.
• Matplotlib: Para visualizar gráficos.

Son externas a Python por lo que tenemos que instalarlas para poder utilizarlas, esa será nuestra primera tarea, empezando por NumPy:

pip install numpy

La clase array de NumPy¶

La programación gráfica se basa en la idea de manipular información almacenada en unas estructuras conocidas como vectores y matrices. En Python la única forma de simular estas estructuras es usando listas y lo malo es que son muy limitadas respecto a las funciones matemáticas que permiten. Numpy viene a solucionar esa carencia ofreciéndonos un nuevo tipo de dato llamado array.

Un array es parecido a una lista en Python y de hecho se pueden crear a partir de ellas:

# Normalmente se suele importar numpy como np ya para ahorrar tiempo
import numpy as np

# Podemos crear un arreglo a partir de
array = np.array([1, 2, 3, 4, 5])

# Y lo mostramos
print(array)

Lo primero que notaremos al mostrar un array por pantalla es que a diferencia de las listas sus elementos no están separados por comas.

Podemos consultar el tipo de la variable:

print(type(array))

Este array formado a partir de una lista se considera un array de una dimensión, también conocido como vector.

Dimensión y forma de un array¶

Podemos consultar la dimensión y forma de un array con sus propiedades ndim y shape:

print(array.ndim)
print(array.shape)

Esto nos devolverá una tupla (4,) haciendo referencia el primer valor a que nuestro array tiene 4 elementos en la primera dimensión, que es la de la anchura.

Ahora bien, si nosotros definimos un array a partir de una lista anidada formada por dos sublistas:

array = np.array([
    [1, 2, 3, 4, 5],
    [6, 7, 8, 9, 10]
])
print(array)
print(array.ndim)
print(array.shape)

Veremos algo interesante, y es que el array se muestra como una tabla de 2 filas con 5 columnas, números que precisamente concuerdan con la forma (2, 5).

Estas estructuras formadas por filas y columnas parecidas a una tabla tienen dos dimensiones, anchura y altura (por eso nos dice que tiene 2 dimensiones). También se conocen como vectores multidimensionales, vectores 2D o matrices.

Podemos consultar el tipo de los arrays.

Tipo de un array¶

Por ejemplo cuando tenemos un array formado por números enteros:

array = np.array([1, 2, 3, 4, 5])
print(array.dtype)

El tipo del array es automáticamente establecido como int32 (enteros de 32 bits).

En cambio si uno de los valores fuera decimal:

array = np.array([1, 2, 3, 4, 5, 6.1234])
print(array.dtype)

Entonces el tipo ya sería float64 (flotantes de 64 bits).

Incluso podríamos almacenar cadenas:

array = np.array(["Hola", "que", "tal"])
print(array.dtype)

Pero en este caso nos indica un tipo extraño llamado <U4. Según la documentación de numpy esto hace referencia a que el array es de tipo Unicode, es decir, es un array de texto.

Esto sucede de igual forma si mezclamos números y textos:

array = np.array(["Hola", 1234, 3.1415])
print(array.dtype)

Ahora nos dice que el tipo es <U6 y si mostramos su contenido veremos que todo son cadenas de texto:

print(array)

Con esto queda claro que los arrays no son listas, sino unas estructuras pensadas para almacenar vectores y matrices, que son conscientes en todo momento de su dimensión, forma y tipo.

Tablas y gráficos¶

Os comenté que podemos mostrar gráficos y tablas, para ello se utilizan las bibliotecas matplotlib y pandas respectivamente. Las trataremos en las próximas secciones, pero vamos a hacer un ejemplo para que veáis como el resultado:

import numpy as np
import pandas as pd

tabla = pd.DataFrame(
    np.random.randint(
        0, 100, size=(4, 3)
    ),
    columns=['Pepe', 'María', 'Juan']
)

tabla

En este fragmente estamos haciendo uso de los dataframes de pandas para manejar una tabla generada a partir de un array con valores aleatorios creado con NumPy.

¿Véis lo que os decía sobre cómo se complementan entre ellas?

Con los gráficos pasa lo mismo, podemos dibujar la tabla usando matplotlib completando así el ciclo del análisis:

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

tabla = pd.DataFrame(
    np.random.randint(
        0, 100, size=(4, 3)
    ),
    columns=['Pepe', 'María', 'Juan']
)

tabla.plot()
plt.show()

Pero no nos adelantemos...

Arrays pregenerados¶

Crear arrays a partir de listas puede ser muy tedioso, por eso numpy integra varias funciones muy útiles para generar arrays de uso común en el álgebra de matrices.

Array de ceros¶

Un array de ceros es cuando todos sus elementos son ceros. Podemos generarlos con el método zeros de Numpy:

import numpy as np
np.zeros(3)

Evidentemente podemos generar arrays multidimensionales, pero para ello tenemos que pasarle al método una lista o tupla con la longitud de sus dimensiones:

np.zeros([3,3])

Array de unos¶

Lo mismo podemos hacer pero utilizando el método ones:

np.ones([3,3])

Array de identidad¶

Los arrays de identidad son matrices cuadradas (con el mismo número de filas que de columnas) donde todos los valores son ceros a excepción de la diagonal donde son unos. Podemos generarlos con el método eye:

np.eye(3)

Las matrices de identidad son muy interesantes ya que sus elementos son siempre cero menos cuando los índices de la fila y la columna son el mismo.

Array de rangos¶

Por último pero no por ello menos importante también es posible generar arrays a partir de un rango de valores. Para hacerlo utilizaríamos el método arange:

# Rango de 0 a 4
np.arange(4)

# Rango 0 a 4 decimal
np.arange(4.)

# Rango de -3 a 4
np.arange(-3, 3)

# Rango de 0 a 20 cada 5 números
np.arange(0, 20, 5)

Operaciones básicas¶

La clase array es muy flexible y permite muchas operaciones entre dos arrays, aunque con algunos requisitos.

Suma¶

Por ejemplo las operaciones suma y resta requieren que los arrays tengan la misma forma, es decir, mismo número y tamaño de las dimensiones.

# %%
import numpy as np

# Dados dos arrays
arr_1 = np.array([1,2,3,4])
arr_2 = np.array([5,6,7,8])

# Los sumamos
arr_1 + arr_2

Si no tienen la misma forma no podemos sumarlos:

arr_3 = np.array([9,10])

arr_2 + arr_3

Resta¶

arr_2 - arr_1

¿Qué ocurriría si restamos un array a si mismo?

arr_1 - arr_1

Pues que obtenemos un array con todos los valores a cero.

Producto¶

En el caso del producto, la divisón y la potencia se pueden operar arrays de las mismas dimensiones si el número de columnas de la primera coincide con el número de filas de la segunda.

arr_1 * arr_2

El producto de arrays se basa en multiplicar cada elemento de una array por el elemento en la misma posición del otro.

• 1x5 = 5
• 2x6 = 12
• 3x7 = 21
• 4x8 = 32

También podemos multiplicar un array por un número:

arr_1 * 2

En este casi sería equivalente a un array con una fila y una columna 1x1:

arr_4 = np.array(2)
arr_1 * arr_4

División¶

arr_1 / arr_2

Igual que el producto, la división entre arrays se basa en dividir cada elemento de un array por el elemento en la misma posición del otro.

• 1/5 = 0.2
• 2/6 = 0.33...
• 3/7 = 0.42...
• 4/8 = 0.5

También podemos dividir todos sus elementos por un número:

arr_1 / 2

• 1/2 = 0.5
• 2/2 = 1
• 3/2 = 1.5
• 4/2 = 2

Algo interesante que podemos hacer con la división es conseguir el arreglo inverso o recíproco dividiendo 1 entre el array:

1 / arr_1

Es equivalente hacer la potencia a -1 del array:

arr_1 ** -1

Lamentablemente no podemos elevar a un entero negativo, pero sí podemos indicar la elevación a -1. e indicar así que queremos usar un decimal:

arr_1 ** -1.

Ya que estamos con las potencias, también podemos hacer potencias entre arrays.

Potencia¶

arr_1 ** arr_2

Como es normal, se basa en realizar la potencia entre los valores que comparten posición en los arrays:

• 1**5 = 5
• 2**6 = 64
• 3**7 = 2187
• 4**8 = 65536

Operaciones en arrays de 2D¶

Todo lo que hemos visto aplica también a los arrays de dos dimensiones:

arr_5 = np.array([[1,2],[3,4]])
arr_6 = np.array([[5,6],[7,8]])

arr_5 + arr_6

Como es normal se basa en realizar la operación entre los valores que comparten posición en los arrays:

[ [1+5, 2+6], [3+7, 4+8] ] = [ [6, 8], [10, 12] ]

De igual forma funcionaría el producto, división y potencia por un número:

arr_5 * 3

[ [1x3, 2x3], [3x3, 4x3] ] = [ [3, 6], [9, 12] ]

Como hemos comentado podemos multiplicar, dividir y potenciar matrices siempre que el número de columnas de la primera coincida con el número de filas de la segunda:

arr_7 = np.array([5,10])

arr_5 * arr_7

[ [1x5, 2x10], [3x5, 4x10] ] = [ [5, 20], [15, 40] ]

Arrays multidimensionales¶

1 dimensión¶

En la programación cuando trabajamos con colecciones de datos uno de los conceptos más importante es el índice.

El índice en los arrays funciona exactamente igual que en las listas, es simplemente un número que hace referencia a la posición del array que queremos consultar o modificar:

import numpy as np

arr = np.arange(0, 50, 5)
arr

Índices¶

La caracterítica más importante de los índices es que se empiezan a contar desde cero, no desde uno, por tanto para acceder al elemento de la primera posición del array utilizaremos el 0:

arr[0]

Si queremos saber el de la quinta posición, simplemente tomamos el 5 y le restamos 1, por tanto sería índice 4:

arr[4]

En Python el índice -1 hace referencia a la última posición de la colección, el -2 al penúltimo, etc.

Así que también podemos utilizar índices negativos en arrays:

arr[-1]

Pero no sirven únicamente para consultar, también sirven para modificar valores:

arr[0] = 99
arr

Slicing¶

La técnica del slicing nos permite acceder y modificar un rango de valores de un array. Se basa en dos índices, uno de inicio y otro de fin separados por dos puntos. Si dejamos los índices vacíos se toman por defecto el principio y el final:

arr[:]

Para conseguir un subarray de los 3 primeros elementos haríamos [:3] o [0:3]:

arr[:3]

Para modificar un rango del array podemos hacerlo de forma masiva con un valor:

arr[1:-1] = 50
arr

Consideraciones importantes¶

Los arrays tienen una característica muy especial y es que se encuentran referenciados en la memoria.

¿Qué significa eso? Pues que a la hora de trabajar con subarrays todos los cambios que hagamos se verán reflejados en el array original. Fijaros...

# Reiniciamos el array a como estaba
arr = np.arange(0, 50, 5)

# Extraemos una subarray
sub_arr = arr[0:4]
sub_arr

Por ahora todo bien, pero vamos a modificar este subarray:

sub_arr[:] = 50

sub_arr

Ahora veamos qué ha ocurrido con el array original:

arr

¡Pues que se también se ha actualizado!

Esto ocurre porque numpy hace una gestión óptima de la memoria y no va a malgastarla creando copias por valor.

Para crear una copia real de un array y no modificar el original, tendremos que utilizar el método copy:

arr = np.arange(0, 50, 5)

cop_arr = arr.copy()

cop_arr

Modificamos la copia...

cop_arr[:] = 50

cop_arr

Y el original debería seguir intacto:

arr

2 dimensiones¶

En la lección anterior vimos como trabajar con arrays de una dimensión, ahora veremos como se trasladan esos conceptos a la segunda dimensión.

Es extremadamente sencillo si nos imaginamos el array como una tabla con filas y columnas.

import numpy as np

arr_2d = np.array(([0,5,10], [15,20,25], [30,35,40]))

arr_2d

Índices¶

Si tenemos dos dimensiones, entonces necesitamos dos índices.

El primer índice hace referencia a la primera dimensión, podemos entenderlo como la fila:

# Primera fila
arr_2d[0]

Ahora para acceder a la segunda dimensión, o columna, utilizaremos un segundo índice. Así podemos acceder a valors individuales:

# Primera fila y primera columna
arr_2d[0][0]

También podemos utilizar los índices negativos para posicionarnos muy fácilmente en la última fila y última columna:

arr_2d[-1][-1]

Utilizando esta lógica podemos cambiar fácilmente la primera columna de la última fila:

arr_2d[-1][0] = 99

arr_2d

Slicing¶

También es posible utilizar slicing, aunque al tener dos dimensiones deberemos hacerlo doblando los indices de inicio y fin separados por una coma.

Por ejemplo, un slicing sin indices buscaría un subarray con todas las filas y columnas:

arr_2d[:,:]

Para conseguir un subarray de las dos primeras filas haríamos:

arr_2d[:2,:]

O uno con la primera columna:

arr_2d[:,:1]

Con esta lógica podemos también modificar los elementos masivamente. Por ejemplo toda la segunda columna:

arr_2d[:,1:2] = 0

arr_2d

Copias¶

Los arrays de dos dimensiones también están referenciados en memoria, por lo que todos los cambios realizados en un subarray se verán reflejados en el original.

Recordad utilizar el método .copy() para crear copias por valor y no por referencia a la memoria.

Fancy index¶

El último concepto importante que veremos sobre los arrays 2d es el fancy index. Esta propiedad de los arrays nos permite trabajar muy cómodamente con las filas de estos arrays.

Por ejemplo, vamos a crear una matriz 5x10 llena de ceros:

arr_2d = np.zeros((5,10))

arr_2d

Ahí tenemos nuestra matriz de 5 filas y 10 columnas.

Hasta ahora sabemos acceder fácilmente a una fila concreta, por ejemplo la 3 (3-1):

arr_2d[2] = 10

arr_2d

¿Pero habría alguna forma de acceder a varias a la vez? Pues sí, con el fancy index, que se basa en pasarle una lista al array haciendo referencia a las filas donde queremos acceder.

Por ejemplo podemos modificar al vuelo la primera, tercera y última fila:

arr_2d[[0,2,-1]] = 99

arr_2d

Incluso podemos utilizarlo en cualquier orden o doblando índices:

arr_2d[[4,0,1,0,4]]

La verdad es que es casi mágico, y todo es por la idea de que realmente las filas simulan sublistas.

De hecho podríamos recorrer este array 2d con un for y cada vez que entramos al bucle estamos en una fila:

for row in arr_2d:
    print(row)

De manera que si quisiéramos darle el mismo valor a cada fila no costaría mucho, sólo deberíamos acceder a través de nuestro índice mágico, que podemos sacarlo por ejemplo con un enumerador:

for i, row in enumerate(arr_2d):
    arr_2d[i] = i

arr_2d

3 y más dimensiones¶

Hasta ahora hemos trabajado los arrays de 1 y 2 dimensiones, así que la pregunta es... ¿Será posible hacer lo mismo con 3 o más dimensiones? Pues sí. ¿Pero cómo se hace?

Creación básica¶

De la misma forma que un array de 2 dimensiones, el truco para crear uno de 3 consiste en anidar listas a 3 niveles de profundidad.

Para entender bien el proceso vamos a recrear los 3 niveles de profundidad paso a paso para un array muy simple de 2x2x2

import numpy as np

# Primer nivel, 2 elementos en ancho
arr_1d = np.array(
    [1, 2]
)
arr_1d

# Segundo nivel, 2 elementos en ancho por 2 de alto,
# 4 elementos en total
arr_2d = np.array([
    [1, 2],
    [3, 4]
])
arr_2d

# Tercer nivel, 2 elementos en ancho por 2 de alto
# por 2 de profundidad, 8 elementos en total
arr_3d = np.array([
    [
        [1, 2],
        [3, 4]
    ],
    [
        [5, 6],
        [7, 8]
    ]
])
arr_3d

Con esto tenemos las 3 dimensiones, pero podemos añadir más.

El concepto es difícil de imaginar, ya que nosotros únicamente percibimos 3 dimensiones, pero si lo entendemos como una ramificación en dónde por cada elemento ahora hay otra lista con dos elementos, entonces no es tan imposible hacernos una idea:

# Cuarto nivel, 2 elementos en ancho por 2 de alto
# por 2 de profundidad por 2 más, 16 en total
arr_4d = np.array([
    [
        [
            [1, 2],
            [3, 4]
        ],
        [
            [5, 6],
            [7, 8]
        ]
    ],
    [
        [
            [9, 10],
            [11, 12]
        ],
        [
            [13, 14],
            [15, 16]
        ]
    ]
])
arr_4d

Creación pre-generada de ceros y unos¶

Evidentemente no siempre vamos a querar crear nuestros arrays de 3 o más dimensiones a mano. También podemos crearlos con las funciones de pre-generación que vimos en la lección 2.

# Array 3d de ceros 2x2x2
arr_3d = np.zeros([2,2,2])
arr_3d

# Array 4d de unos 2x2x2x2
arr_4d = np.ones([2,2,2,2])
arr_4d

Creación con reshape¶

Reshape es una función que sirve para reformar las dimensiones y sus tamaños.

Por ejemplo podemos reformar una matriz de 3x3 a partir de un rango de 9 elementos:

arr_2d = np.arange(9).reshape(3,3)
arr_2d

Evidentemente tenemos que seguir un patrón lógico, y es que el número de elementos tiene que concordar con el tamaño de las dimensiones multiplicadas.

# Esto no funcionará: 9 != 3x3x3
arr_3d = np.arange(9).reshape(3,3,3)
arr_3d

# Esto sí que funcionará: 27 == 3x3x3
arr_3d = np.arange(27).reshape(3,3,3)
arr_3d

Arrays transpuestos¶

Una matriz transpuesta es una matriz que refleja a otra, de manera que las columnas se vuelven filas y las filas columnas:

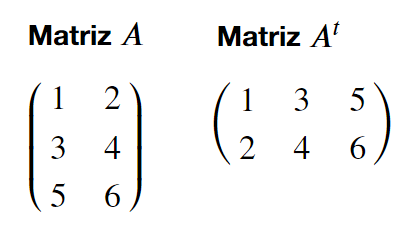
Evidentemente la transpuesta de una matriz transpuesta es equivalente a la matriz original:

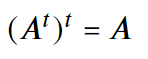
Lo interesante es que con numpy podemos conseguir el array transpuesto muy fácilmente.

import numpy as np

arr = np.array([[1,2,3],[4,5,6]])
arr

# Tranpuesta
arr.T

# Tranpuesta de la transpuesta
arr.T.T

Por cierto, la función swapaxes sirve precisamente para intercambiar la posición de los dos ejes de un array, así que sirve para lo mismo:

# Intercambiar las filas por las columnas
arr.swapaxes(0,1)
arr.swapaxes(1,0) # Es lo mismo

Evidentemente también podemos encontrar el array transpuesto de un array de 3 o más dimensiones:

# Creamos un array 3d
arr_3d = np.arange(8).reshape(2,2,2)
arr_3d

# Buscamos el array transpuesto
arr_3d.T

O intercambiar los ejes con swapaxes, por ejemplo la primera dimensión por la tercera, que en nuestro caso sería equivalente al array transpuesto:

arr_3d.swapaxes(0,2)

En cambio no lo sería intercambiar la primera por la segunda:

arr_3d.swapaxes(0,1)

Funciones universales¶

En esta lección vamos a ver algunas de las funciones universales de la clase array de Numpy. Se llaman universales porque sirven para aplicar funciones matemáticas comunes a los elementos del array.

Podemos encontrar operaciones matemáticas, trigonométricas, flotantes, comparativas y de cambios de bits.

En este enlace a la documentación oficial encontraréis el listado completo con ejemplos de uso.

Por ahora vamos a practicar algunas de las más comunes.

Matemáticas¶

import numpy as np

# Declaramos un par de arrays de prueba
arr_1 = np.arange(1,6)
arr_2 = np.array([-3,7,3,13,0])

# Suma
np.add(arr_1, arr_2)

# Resta
np.subtract(arr_2, arr_1)

# Raiz cuadrada
np.sqrt(arr_1)

# Potencia
np.power(arr_1, 2)

# Signo
np.sign(arr_1)

Trigonométricas¶

# Seno
np.sin(arr_1)

# Tangente
np.tan(arr_1)

# Grados a radianes
np.deg2rad(arr_1)

Comparativas¶

# Máximo
np.maximum(arr_1, arr_2)

# Igual
np.equal(arr_1, arr_2)

# Mayor
np.greater(arr_1, arr_2)

Flotantes¶

# Declaramos un tercer array de prueba
arr_3 = np.array([3.14, 2.57, -6.4, 0.47, 5.5])

# Valor absoluto
np.fabs(arr_3)

# Techo (redondeo entero siempre al alza)
np.ceil(arr_3)

# Suelo (redondeo entero siempre a la baja)
np.floor(arr_3)

Funciones aleatorias¶

Ya que estamos repasando funciones no podemos olvidar las funciones aleatorias de numpy, encontradas en el módulo random.

En este enlace a la documentación oficial encontraréis el listado completo con ejemplos de uso.

Tenemos funciones para generar arrays con datos aleatorios y permutaciones. También hay muchas enfocadas a generar muestras de distribuciones de probabilidadpensadas para visualizar estadística.

Vamos a practicar algunas de las dos primeras.

Datos aleatorios¶

import numpy as np

# Número decimal entre 0 y 1
np.random.rand()

# Array 1D de decimales entre 0 y 1
np.random.rand(4)

# Array 2D de decimales entre 0 y 1
np.random.rand(4,2)

# Array 3D de decimales entre 0 y N
np.random.uniform(10, size=[2,2,2])

# Array 4D de decimales entre -N y M
np.random.uniform(-10, 10, size=[2,2,2,2])

# Número entero entre 0 y N
np.random.randint(10)

# Array de enteros entre 0 y N
np.random.randint(10, size=[3,2])

# Array de enteros entre -N y M
np.random.randint(-10, 10, size=[3,2])

# Array uniforme (con curva gaussiana)
np.random.normal(size=100)

Permutaciones¶

arr = np.arange(10)

# Desordenar un array (lo cambia)
np.random.shuffle(arr)
arr

# Generar secuencia permutada a partir de un número
np.random.permutation(10)

Filtrado de arrays¶

En esta lección vamos a repasar algunas funciones para filtrar nuestros arrays.

Si queréis más información sobre las funciones disponibles no olvidéis pasaros por la documentación oficial en este enlace.

Filtro unique¶

Devuelve un array de una dimensión borrando todos los elementos duplicados.

# %%
import numpy as np

# Generamos un array con números aleatorios repetidos
arr = np.random.randint(0, 4, 10)
arr

# Aplicamos el filtro unique
np.unique(arr)

Filtro in1d¶

Devuelve un array de una dimensión indicando si los elementos de una lista se encuentran en un array.

np.in1d([-1, 3, 2], arr)

Filtro where¶

Esta función sirve para generar un array filtrado a partir de una condición y un valor por defecto.

# Generamos un array con números aleatorios
arr_1 = np.random.uniform(-5, 5, size=[3,2])
arr_1

# Creamos un filtro que establece los negativos a 0
arr_2 = np.where(arr_1<0, 0, arr_1)
arr_2

# Añadimos otro filtro que establece los positivos a 1
arr_2 = np.where(arr_2>0, True, arr_2)
arr_2

Filtros booleanos¶

# Comprobar si todos los elementos de un array son True
arr_bool = np.array([True,True,True,False])
arr_bool.all()

# Comprobar al menos un elemento del array es True
arr_bool = np.array([True,True,True,False])
arr_bool.any()

# También aplican a un eje en particular
arr_bool = np.array([[True,True],[False,True],[True,True]])
arr_bool

# Columas verdaderas
arr_bool.all(0)

# Filas verdaderas
arr_bool.all(1)

Métodos internos¶

En esta lección vamos a repasar algunos métodos matemáticos y de ordenación que incluye la clase array.

Para más información tenéis como siempre la documentación oficial en este enlace.

Métodos matemáticos¶

import numpy as np

# Generamos un array de 2*3 con números aleatorios
arr = np.arange(1,7).reshape(2,3)
arr

# Sumatorio
arr.sum()

# Media
arr.mean()

# Desviación estándard
arr.std()

# Varianza
arr.var()

Métodos de ordenación¶

# Ordenar un array
arr = np.random.randint(-10,10,[3,3])
arr

# Ordenar elementos automáticamente (se ordenan en horizontal y se actualiza el array)
arr.sort()
arr

# Ordenar verticalmente utilizando el eje 0
arr.sort(0)
arr

Arrays y persistencia¶

Para despedir el curso vamos a aprender algunas funciones muy útiles que nos permitirán almacenar nuestros arrays en ficheros. Vienen bien si estamos trabajando y necesitamos almacenar nuestros datos para recuperarlos en otro momento y hacer uso de ellos.

Veremos dos métodos, el clásico en ficheros binarios y la variante en formato de texto. La diferencia entre ambos formatos es que los primeros no se pueden abrir con un editor de texto y editarlos, pero los segundos sí, así que permiten hacer cambios en vivo. A cambio los ficheros binarios pueden almacenar varios arrays y los ficheros de texto únicamente un array por fichero, así que utilizad las dos formas dependiendo de vuestros intereses.

Para más información sobre la persistencia buscad la sección pertinente en la documentación oficial en este enlace.

Guardado binario¶

import numpy as np

arr_1 = np.random.randint(0,4,[3,3])
arr_1

# Para guardarlo utilizamos la ruta y la extensin .npy
np.save('arr_1.npy', arr_1)

En esto punto tendríamos en el mismo directorio donde hemos ejecutado el comando el fichero array.npy. Si indicamos un directorio hasta el fichero lo crearemos ahí, pero tenemos que estar seguros de que el directorio existe y de que tengamos permisos para escribir.

# Ahora eliminamos el array  para asegurarnos de que ya no existe
del(arr_1)
arr_1

# Y lo cargamos de nuevo
arr_1 = np.load('arr_1.npy')
arr_1

De esta forma podemos guardar y leer un array en un fichero, pero podemos guardar y recuperar varios a la vez:

arr_2 = np.random.randint(-4,0,[3,3])

# Utilizaremos savez para guardar de forma comprimida con la extensión .npz
# Especificaremos una clave para cada array que queramos guardar
np.savez('arrays.npz', arr_1=arr_1, arr_2=arr_2)

# Ahora los borramos
del(arr_1)
del(arr_2)

# Y los cargamos de nuevo
arrays = np.load('arrays.npy')
arrays

Como véis el objeto recuperado es un NpzFile, en realidad es como un diccionario así que podemos recuperar los arrays a partir del nombre con que los hemos guardado:

arrays['arr_1']

arrays['arr_2']

Guardado en texto¶

Básicamente se hace de la misma forma, pero las funciones cambian:

• Para guardar de save -> savetxt
• Para cargar de load -> loadtxt

# Creamos un array de prueba
arr_3 = np.random.randint(-10,10,[3,3])
arr_3

# Lo guardamos en un fichero de texto, el formato es libre
np.savetxt('arr_3.txt', arr_3)

Por defecto los arrays en ficheros de texto se guardan con filas separadas por saltos de línea y columnas separadas por espacios:

2.000000000000000000e+00 -4.000000000000000000e+00 -6.000000000000000000e+00
7.000000000000000000e+00 -5.000000000000000000e+00 -7.000000000000000000e+00
-1.000000000000000000e+01 -4.000000000000000000e+00 -1.000000000000000000e+01

Pero podemos establecer el separador a voluntad:

# Columnas con ,
np.savetxt('arr_3.txt', arr_3, delimiter=',')

Esto generaría algo como:

-6.000000000000000000e+00,9.000000000000000000e+00,-8.000000000000000000e+00
0.000000000000000000e+00,3.000000000000000000e+00,6.000000000000000000e+00
4.000000000000000000e+00,0.000000000000000000e+00,4.000000000000000000e+00

No importa cómo lo guardemos, lo importante es que a la hora de recuperarlos indiquemos los separadores si los hemos cambiado:

# Lo borramos
del(arr_3)

# Lo cargamos indicando el separador (si lo hemos cambiado)
arr_3 = np.loadtxt('arr_3.txt', delimiter=',')
arr_3

Última edición: 17 de Julio de 2022