Operadores bit a bit en C++¶
Las operaciones bit a bit permiten manejar la información a nivel de hardware.
La biblioteca <bitset> nos ofrece un conjunto de funcionalidades para trabajar con bits, por ejemplo para hacer conversiones entre enteros y binarios:
#include <iostream>
#include <bitset>
int main()
{
unsigned short int numero{15}; // 15 en binario es 1111
std::cout << std::bitset<8>(numero) << std::endl;
std::bitset<8> bits("1111"); // 1111 en decimal es 15
std::cout << bits.to_ulong() << std::endl;
}
Cambio de bit¶
Una de las operaciones binarias básicas es el cambio de bit, el cuál implica un corrimiento de bits ya sea a la izquierda o a la derecha.
Por ejemplo, tomando el binario 01111 (15) un corrimiento a la izquierda implicaría daría como resultado el número 11110 (30). Este corrimiento se realiza con el operador binario <<, que en asignación quedaría <<=:
bits <<= 1; // Corrimiento 1 bit izquierda, 01111 (15) -> 11110 (30)
std::cout << bits << " (" << bits.to_ulong() << ")" << std::endl;
Así mismo el corrimiento a la derecha sería >>, en asignación >>=. Partiendo por ejemplo de 11110 (30), correr a la derecha 1 bit daría como resultado 01111 (15):
bits >>= 1; // Corrimiento 1 bit derecha, 11110 (30) -> 01111 (15)
std::cout << bits << " (" << bits.to_ulong() << ")" << std::endl;
El cambio de bit implica se resume en estas tres reglas:
- Hacia la izquierda multiplica el número por
2^n. - Hacia la derecha divide el número entre
2^n. - Esto no se cumplirá si se pierde un 1 a la izquierda o derecha.
Ambos operadores también pueden utilizarse con números enteros:
std::cout << (100 << 1) << std::endl; // 2^1 = 2 -> 100*2 = 200
std::cout << (100 >> 1) << std::endl; // 2^1 = 2 -> 100/2 = 50
std::cout << (100 << 2) << std::endl; // 2^2 = 4 -> 100*3 = 300
std::cout << (100 >> 2) << std::endl; // 2^2 = 4 -> 100/3 = 33
std::cout << (100 << 3) << std::endl; // 2^3 = 8 -> 100*8 = 800
std::cout << (100 >> 3) << std::endl; // 2^3 = 8 -> 100/8 = 12.5 (12)
Operadores lógicos¶
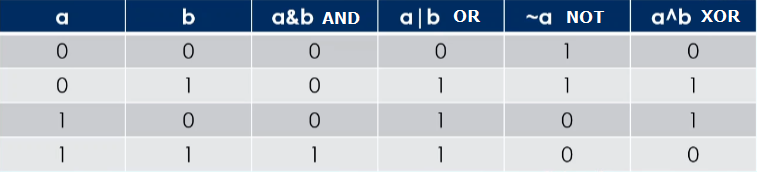
Otra forma de operar los bits es mediante los operadores lógicos bit a bit & (AND), | (OR), ~(NOT) y ^ (XOR), con sus variantes en asignación &=, |= y ^=.
El resultado de las operaciones lógicas entre dos bits se ilustra en la siguiente tabla:
std::bitset<16> b1("10101010"); // 170
std::bitset<16> b2("01010101"); // 85
std::cout << (b1 | b2) << " (" << (b1 | b2).to_ulong() << ")\n"; // 255
std::cout << (b1 & b2) << " (" << (b1 & b2).to_ulong() << ")\n"; // 0
std::cout << (b1 ^ b2) << " (" << (b1 ^ b2).to_ulong() << ")\n"; // 255
std::cout << (~b1) << " (" << (~b1).to_ulong() << ")\n"; // 65365

Máscaras¶
Una utilidad de los operadores bit a bit es para trabajar mediante máscaras. Una máscara es una secuencia de bits, por ejemplo un byte (8 bits), la cuál podemos aplicar a otro byte para realizar en él distintas operaciones:
- Establecer posiciones de bit.
- Reiniciar posiciones de bit.
- Comprobar posiciones de bit.
- Alternar posiciones de bit.
Empecemos definiendo unas cuantas máscaras para realizar algunas operaciones:
std::bitset<8> mask_bit_1("00000001"); // 1
std::bitset<8> mask_bit_2("00000010"); // 2
std::bitset<8> mask_bit_3("00000100"); // 4
std::bitset<8> mask_bit_4("00001000"); // 8
std::bitset<8> mask_bit_5("00010000"); // 16
std::bitset<8> mask_bit_6("00100000"); // 32
std::bitset<8> mask_bit_7("01000000"); // 64
std::bitset<8> mask_bit_8("10000000"); // 128
Supongamos que empezamos con un byte con todos los bits apagados (en 0):
std::bitset<8> byte ("00000000"); // 0
Si queremos establecer bits (1) podemos aplicar máscaras con: |= mascara:
byte |= mask_bit_1 | mask_bit_3 | mask_bit_6;
std::cout << byte << std::endl; // 00100101 (37)
Si queremos reiniciar bits (0) podemos aplicar máscaras con: &= (~mascara):
byte &= ~(mask_bit_1 | mask_bit_3); //~mask_bit_1 & ~mask_bit_3
std::cout << byte << std::endl; // 00100000 (32)
Para comprobar el si un se encuentra activado (1) o desactivado (0) podemos aplicar la máscara: (& mascara) >> posicion:
std::cout << "bit 1: " << ((byte & mask_bit_1) >> 0) << std::endl; // 00000000
std::cout << "bit 6: " << ((byte & mask_bit_6) >> 5) << std::endl; // 00000001
Esto es un poco incómodo así que podemos hacer una igualidad a 1 y activar la visualización de binario a booleano:
std::cout << std::boolalpha;
std::cout << "bit 1: " << (((byte & mask_bit_1) >> 0) == 1) << '\n';
std::cout << "bit 6: " << (((byte & mask_bit_6) >> 5) == 1) << '\n';
Por último podemos alternar los bits (0 a 1 y 1 a 0) mediante el operador xor: ^mascara:
byte ^= (mask_bit_1 | mask_bit_2 | mask_bit_3 | mask_bit_6);
std::cout << std::noboolalpha << byte << std::endl ; // 00000111 (7)
Un ejemplo práctico del uso de las máscaras es para trabajar con colores hexadecimales.
Todos los colores hexadecimales pueden generarse a partir de la suma de los tres colores básicos en el patrón RGB rojo 0xFF0000, verde 0x00FF00 y azul 0x0000FF.
Si definimos estos tres valores como máscaras podemos saber la conversión de hexadecimal a entero para cualquier color RGB:
const unsigned int red_mask{0xFF0000}; // primer byte
const unsigned int green_mask{0x00FF00}; // segundo byte
const unsigned int blue_mask{0x0000FF}; // tercer byte
Para ello deberemos aplicar las máscaras al principio de cada byte de un color RGB (0, 8, 16):
unsigned int color{0xFF12EF}; // color RGBA cualquiera
std::cout << "Rojo: " << ((color & red_mask) >> 16) << std::endl; // 255
std::cout << "Verde: " << ((color & green_mask) >> 8) << std::endl; // 18
std::cout << "Azul: " << ((color & blue_mask) >> 0) << std::endl; // 239
Como curiosidad el color RGB (255, 18, 239) o #FF12EF es este:
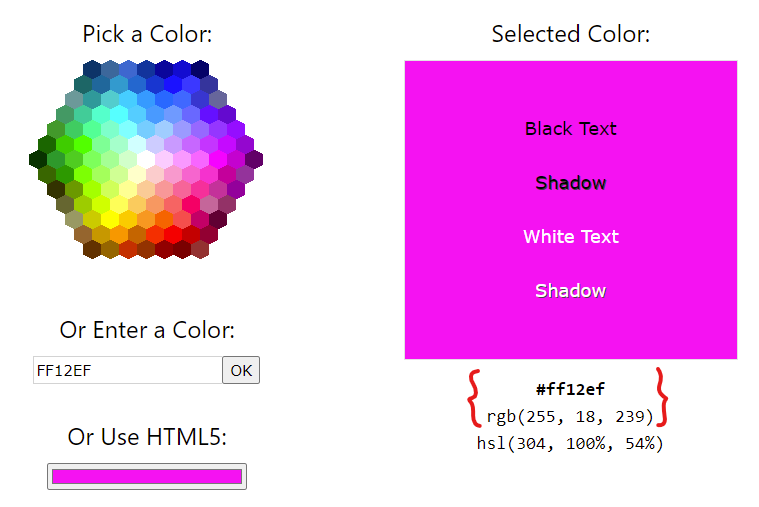
Última edición: 09 de Mayo de 2022
