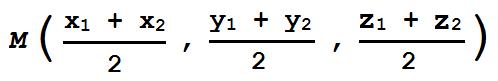Distancia entre dos puntos (2D y 3D)¶

Cuando programamos videojuegos una de las cosas que normalmente necesitamos saber es la distancia entre dos puntos de la pantalla. Podrían ser dos objetos que van a chocar o la IA (Inteligencia Artificial) de un enemigo que a cierta distancia de nuestro personaje nos atacará.

No importa la situación, lo importante es ser capaces de calcular esta distancia entre dos puntos, y la forma más simple de hacerlo es utilizando el Teorema de Pitágoras.

Teorema de Pitágoras¶

Este teorema nos dice que para cualquier triángulo rectángulo (con un ángulo de 90º) la suma de sus catetos al cuadrado es igual a la hipotenusa al cuadrado:

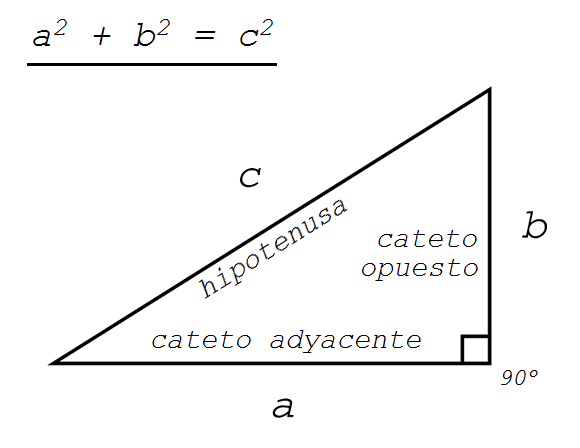
Por consiguiente a la inversa se puede deducir que si… a,b y c son las longitudes de los tres lados de un triángulo y a2 + b2 = c2  entonces el triángulo es rectángulo con una hipotenusa de longitud c.

Si aplicamos este conocimiento a una pendiente entre dos puntos P1 y P2 nos daremos cuenta que la propia pendiente es la hipotenusa de un triángulo rectángulo, siendo el tercer vértice un punto T con las coordenadas (x2,y1):

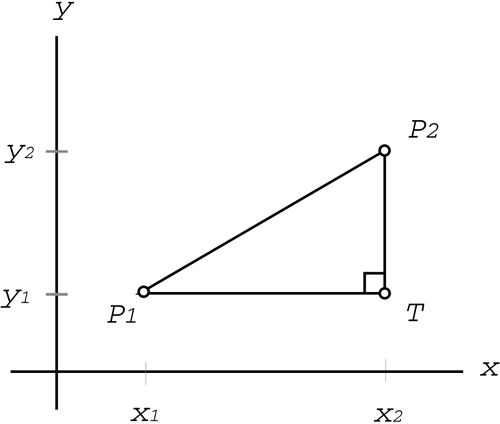
Traduciendo la figura anterior al teorema de Pitágoras tendríamos que:

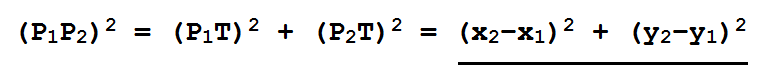
Distancia entre dos puntos 2D¶

De esta forma podríamos calcular la distancia entre dos puntos como si fuera la hipotenusa de un triángulo rectángulo, lo que nos da la fórmula de la distancia en 2D:

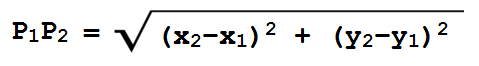
Por ejemplo, si queremos determinar la distancia entre dos objetos en el plano centrados en las coordenadas (25,80) y (50,45) aplicaremos la fórmula así:

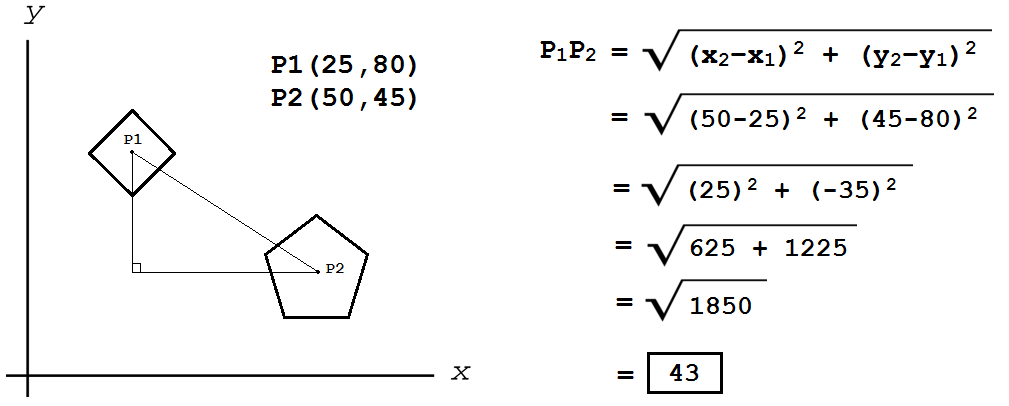
Punto intermedio 2D¶

En nuestros videojuegos, a veces nos vemos en la necesidad de calcular el punto intermedio entre dos objetos. Para ello podemos utilizar la siguiente fórmula:

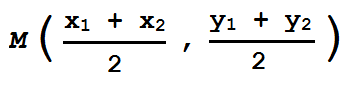
Por ejemplo para determinar el punto intermedio entre dos objetos centrados en las coordenadas (40,80) y (50,50) lo calcularemos así:

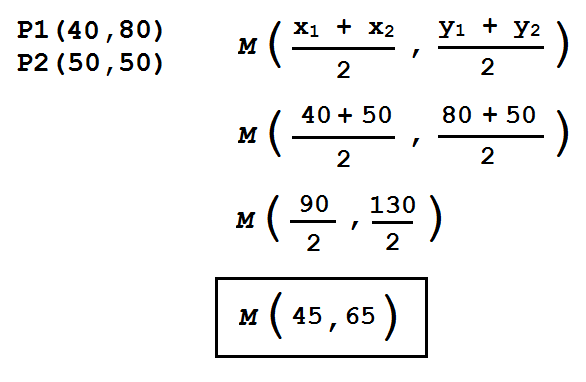
Distancia entre dos puntos 3D¶

Cuando hablamos de tres dimensiones las fórmulas no varían mucho, sólo hay que tener en cuenta el componente z. La fórmula para la distancia sería:

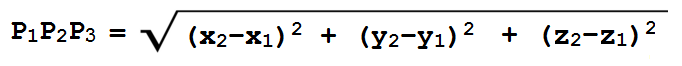
Punto intermedio 3D¶

Mientras que para el punto medio quedaría: