Parábolas (Ecuaciones)¶

Si has jugado alguna vez a fútbol o baloncesto, entonces sabes de buena mano que la bola nunca se mueve en línea recta, sino que más bien lo hace siguiendo una especie de curva o arco. De hecho, cualquier proyectil lo que hace es seguir lo que se conoce como un movimiento parabólico.

Se utiliza parábola para definir una curva o arco simétrico. No importa si es arriba-abajo, izquierda-derecha o al revés, porque un lado de la parábola siempre será un reflejo del otro:

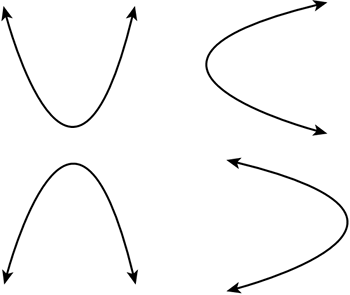
Evidentemente las parábolas también son líneas así que tienen su propia ecuación. Los dos componentes necesarios para determinar la ecuación de una parábola son:

• El vértice: que es la punta del arco.
• El eje de simetría: que pasa por el vértice y divide la parábola por la mitad para que cada lado sea un reflejo del otro.

También hay dos formas para la ecuación, una para la versión arriba-abajo con eje vertical de simetría, y otra para la versión de lado con eje horizontal de simetría:

Parábola con Eje Vertical

Parábola con Eje Horizontal

Es posible hacerse una idea de cómo es una parábola sin necesidad de calcular la ecuación, sólo debes tener en cuenta algunas características. Primero:

Si la ecuación está en forma y = a (x-h)² + k, significa que se abre hacia arriba o hacia abajo y debes probar diferentes valores de x para resolver las y.

• Si está en forma x = a (y-k)² + h, es que se abre hacia los lados y debes probar diferentes valores de y para resolver las x.

En segundo lugar, la constante a determina en qué dirección se abre la parábola:

• Si a es un número positivo, la parábola se abre hacia arriba si está en forma y = a (x - h)² + k, o se abre a la derecha si es x = a (y-k)² + h.
• Si a es negativo, la parábola se abre hacia abajo o hacia la izquierda.

Y también el ancho de la abertura:

• Cuanto más cerca de 0 se encuentre a más ancha es la abertura de la parábola.
• Cuanto más lejos de 0 se encuentre a más delgada será la abertura.

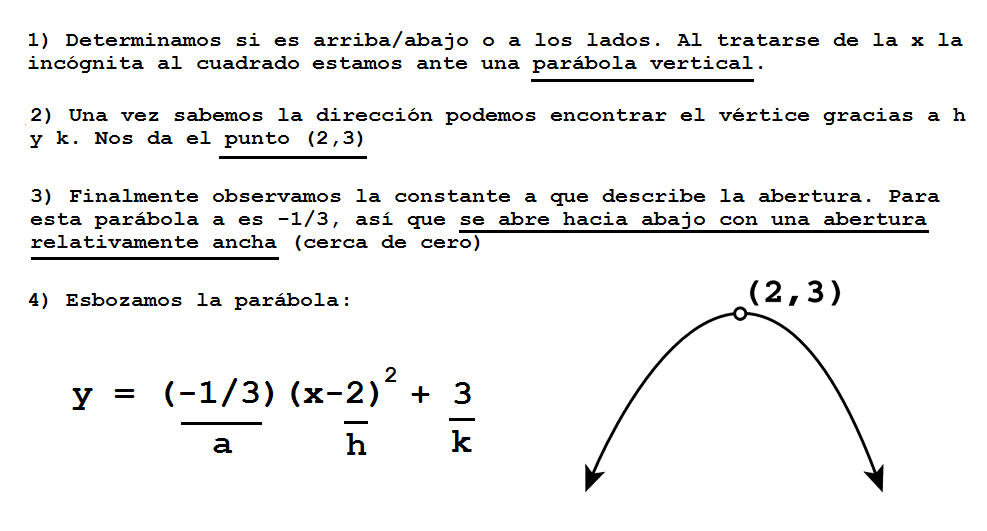
Con estas referencias es fácil hacerse una idea del tipo de parábola que hay que dibujar únicamente observando su ecuación. En el siguiente ejemplo vemos los pasos para esbozar la parábola y = (-1/3)(x-2)² + 3 al vuelo sin hacer cálculos:

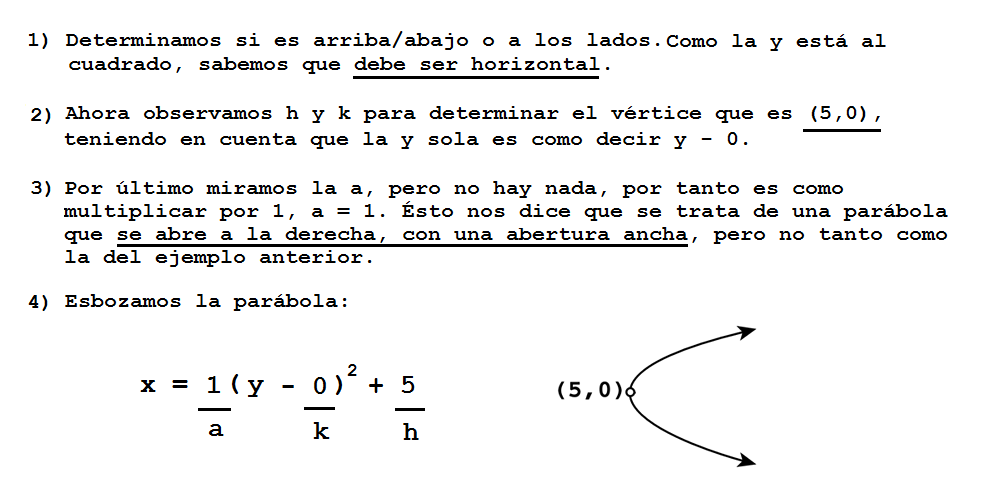
Por último haremos otro ejemplo con la parábola x = y² + 5: