Programando una tortuga con OpenGL¶
Unas de las prácticas más interesantes que he tenido el placer de realizar con el fin de aprender OpenGL ha sido crear mi propia tortuga y dibujar fractales con ellas.
Turtle es un módulo de Python para dibujar primitivas que también se puede encontrar como entorno aislado en https://pythonturtle.org/.
La tortuga es esencialmente una pluma para dibujar sobre un lienzo mediante instrucciones. Implementa diferentes funciones para avanzar hacia adelante, rotar sobre si misma, cambiar el color, levantar la pluma, etc.
Es una forma genial de aprender a programar visualmente y crear un programa que sirva para ello es una de las mejores prácticas posibles.
Estructura básica¶
Vamos a empezar con un proyecto ya preparado con una ventana de 600x600 y mismo tamaño de espacio ortográfico pero de -300 a 300 en cada eje, esto nos permitirá partir con la tortuga en el origen (0,0):
import sys
import math
import numpy as np
import pygame as pg
sys.path.append('..')
from res.App import App
from OpenGL.GL import *
from OpenGL.GLU import *
class Point:
def __init__(self, x=0, y=0):
self.x = x
self.y = y
class GLUtils:
@staticmethod
def InitOrtho(left, right, top, bottom):
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
gluOrtho2D(left, right, top, bottom)
@staticmethod
def PrepareRender():
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
class OpenGLApp(App):
def Setup(self):
GLUtils.InitOrtho(-300, 300, -300, 300)
def Render(self):
GLUtils.PrepareRender()
if __name__ == '__main__':
app = OpenGLApp("Tortuga con OpenGL", 600, 600, 60)
app.Run()

Vamos a implementar la tortuga en su propia clase Turtle que contará con una posición que será un punto (0,0). Le añadiremos un método de clase LineTo para trazar una línea desde su posición actual hasta la nueva posición que pasemos al método y luego cambiaremos su posición actual a la nueva posición:
class Turtle:
pos = Point(0, 0)
@classmethod
def LineTo(cls, x, y):
glLineWidth(2)
glBegin(GL_LINE_STRIP)
glVertex2f(Turtle.pos.x, Turtle.pos.y)
glVertex2f(x, y)
glEnd()
cls.pos.x = x
cls.pos.y = y
Simplemente llamaremos al método de la clase Turtle, que al ser de clase no requiere crear una instancia y podemos usar la propia definición de clase:
class OpenGLApp(App):
def Setup(self):
GLUtils.InitOrtho(-300, 300, -300, 300)
def Render(self):
GLUtils.PrepareRender()
Turtle.LineTo(100, 100)
Si ejecutamos el programa se trazará una pequeña línea desde el centro pero rápidamente desaparecerá. Esto se debe a que en el primer ciclo del bucle la tortuga se mueve de (0,0) a (10,10) pero después ya se encuentra en (10, 10) y por tanto no se mueve ni se dibuja nada.
Si creamos un método para reiniciar la posición de la tortuga a (0,0) en cada fotograma se dibujará el movimiento en cada ciclo:
class Turtle:
@classmethod
def Reset(cls):
cls.pos = Point(0, 0)
class OpenGLApp(App):
def Render(self):
GLUtils.PrepareRender()
Turtle.Reset()
Turtle.LineTo(100, 100)

Moviéndonos a otras posiciones podemos dibujar una forma:
class OpenGLApp(App):
def Render(self):
GLUtils.PrepareRender()
Turtle.Reset()
Turtle.LineTo(100, 100)
Turtle.LineTo(100, 200)
Turtle.LineTo(200, 100)
Turtle.LineTo(100, 100)
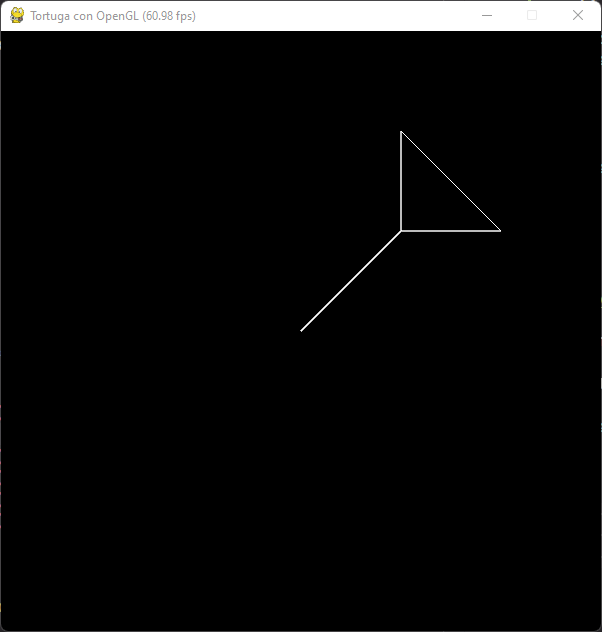
Sin embargo una tortuga no funciona así, la tortuga solo puede moverse adelante y para ir en otro dirección debe girar sobre sí misma.
Así que necesitamos manejar la dirección hacia donde mira nuestra tortuga y para ello necesitamos un vector. Como OpenGL funciona en 3D necesitaremos un vector para almacenar los componentes x, y y z:
class Vector3:
def __init__(self, x=0, y=0, z=0):
self.x = x
self.y = y
self.z = z
Crearemos uno de estos para la dirección de la tortuga donde inicialmente la dirección será hacia arriba, es decir 1 en el eje y. Su valor también lo reiniciaremos en Reset:
class Turtle:
pos = Point(0, 0)
dir = Vector3(0, 1, 0)
@classmethod
def Reset(cls):
cls.pos = Point(0, 0)
cls.dir = Vector3(0, 1, 0)
Por cierto, dir es una función interna de Python pero la vamos a sobreescribir porque tampoco tengo intención de utilizarla.
A continuación vamos a crear un método que substituirá a LineTo para movernos y lo hará solo hacia adelante, se llamará Forward. Multiplicará el vector de dirección por una longitud y lo sumará a la posición actual:
@classmethod
def Forward(cls, distance):
dest = Point()
dest.x = cls.pos.x + cls.dir.x * distance
dest.y = cls.pos.y + cls.dir.y * distance
cls.LineTo(dest.x, dest.y)
Así podremos mover la tortuga 100 píxeles adelante:
class OpenGLApp(App):
def Render(self):
GLUtils.PrepareRender()
Turtle.Reset()
Turtle.Forward(100)
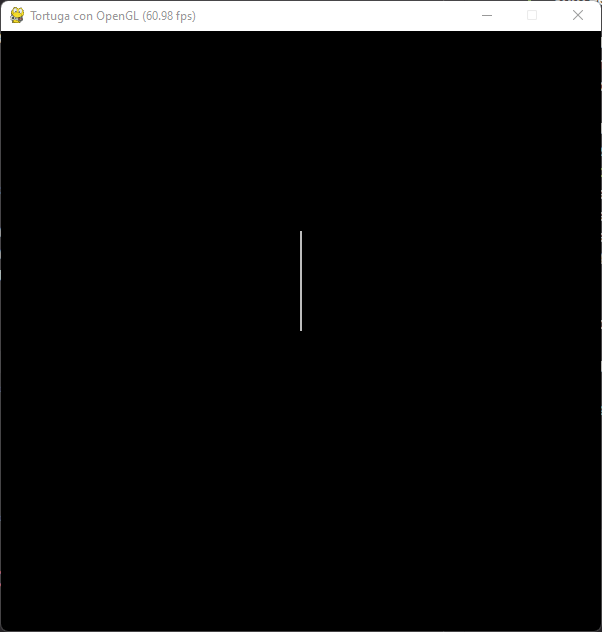
Rotación y movimiento¶
Para rotar la tortuga debemos rotar el vector de dirección formado por tres componentes, pero debemos elegir sobre qué eje rotar. En el espacio tridimensional no es lo mismo rotar sobre x, que y o z tal como muestra esta imagen:
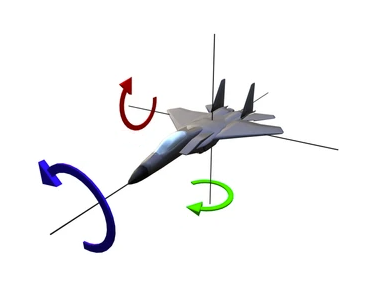
Para rotar la tortuga en nuestro espacio lo que tenemos que hacer es aplicar la rotación sobre el eje z. Este eje representa la profundidad y apunta directamente hacia nosotros como saliendo de la pantalla, sería la flecha azul en la figura de la avisón.
La rotación es una transformación lineal que explico en detalle en mis apuntes sobre gráficos 3D. Me limitaré a recuperar la fórmula, si queréis más detalles echad un vistazo a mis apuntes:
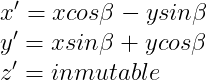
Sería perfecto que la propia clase Vector3 tenga un método para rotar sobre su eje z un cierto ángulo, que por cierto debe ser aplicado en radianos, por lo que realizaremos una conversión al ángulo con grados enviado:
class Vector3:
def RotateZ(self, angle):
angle = np.radians(angle) # ángulo a radianos
rotatedX = self.x * np.cos(angle) - self.y * np.sin(angle)
rotatedY = self.x * np.sin(angle) + self.y * np.cos(angle)
self.x = rotatedX
self.y = rotatedY
En la tortuga implementaremos el método Rotate para aplicar la rotación al vector de dirección:
@classmethod
def Rotate(cls, angle):
cls.dir.RotateZ(angle)
Ahora podemos movernos hacia adelante, rotar y movernos otra vez:
def Render(self):
GLUtils.PrepareRender()
Turtle.Reset()
Turtle.Forward(100)
Turtle.Rotate(90)
Turtle.Forward(200)

Bien, pero ¿notáis algo extraño? Bueno, al rotar estamos haciéndolo en sentido antihorario. ¿Por qué sucede esto? OpenGL se implementa sobre la conocida regla de la mano izquierda, donde el eje z aumenta hacia adentro de la pantalla (esto también lo explico más en detalle en mis apuntes sobre gráficos 3D):
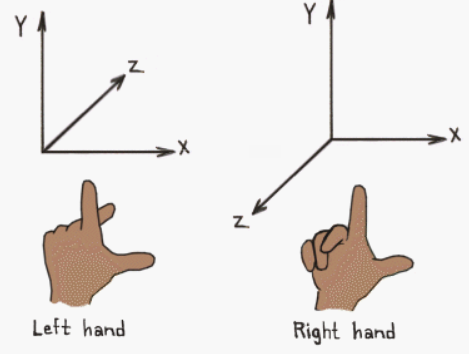
En cualquier caso si queremos obtener el efecto contrario para rotar en sentido horario tendremos que negar el ángulo de rotación, tan sencillo como hacer:
@classmethod
def Rotate(cls, angle):
cls.dir.RotateZ(-angle)
Ahora la rotación será acorde a lo que nuestra lógica podría esperar:

Ahora, por si en algún momento queremos que la tortuga se desplace a otro lugar sin trazar una línea, podemos añadir el método MoveTo donde simplemente actualiz su posición:
@classmethod
def MoveTo(cls, x, y):
cls.pos.x = x
cls.pos.y = y
Así podemos dejar de dibujar, mover la tortuga a otro punto y seguir dibujando:
def Render(self):
GLUtils.PrepareRender()
Turtle.Reset()
Turtle.Forward(100)
Turtle.Rotate(90)
Turtle.Forward(200)
Turtle.MoveTo(-50, -100)
Turtle.Rotate(180)
Turtle.Forward(100)
Turtle.Rotate(45)
Turtle.Forward(100)
Turtle.Rotate(45)
Turtle.Forward(100)

Y ya está, aunque parezca mentira una tortuga no hace muchas más cosas. Podríamos añadir métodos para cambiar el color del trazo o el tamaño, pero esencialmente en esto se basa el funcionamiento.
Con algo ingenio, matemáticas y algún bucle podemos dibujar polígonos fácilmente:
def Render(self):
GLUtils.PrepareRender()
Turtle.Reset()
Turtle.MoveTo(-150, -50)
for i in range(10):
Turtle.Forward(100)
Turtle.Rotate(360/10)

O figuras como estrellas:
def Render(self):
GLUtils.PrepareRender()
Turtle.Reset()
Turtle.MoveTo(0, -150)
for i in range(20):
Turtle.Forward(300)
Turtle.Rotate(170)

Sistemas de Lindenmayer¶
Un fractal es un objeto geométrico cuya estructura básica, fragmentada o aparentemente irregular, se repite a diferentes escalas:

Un sistema de Lindenmayer es una gramática formal (un conjunto de reglas y símbolos) utilizados para modelar el proceso de crecimiento de las plantas y la morfología de una variedad de organismos. Fueron introducidos y desarrollados en 1968 por el biólogo y botánico teórico húngaro Aristid Lindenmayer.
La naturaleza recursiva de las reglas de los sistemas-L conduce a la autosemejanza y por tanto facilita la descripción de formas tipo fractales. Los modelos de plantas y formas orgánicas de aspecto natural son fáciles de definir: al incrementarse el nivel de recursión la forma crece lentamente y se vuelve más compleja. Los sistemas de Lindenmayer también son populares en la generación de vida artificial.

Introducción a parte, vamos a desarrollar nuestro propio sistema-L el cuál definirá una serie de reglas e instrucciones que la tortuga seguirá para trazar diferentes figuras (para una explicación detallada echad un vistazo a la Wikipedia).
Nuestro sistema tendrá una variable axiom con una cadena que representará el estado inicial y un conjunto de reglas rules que explicarán cómo reemplazar los valores del axioma.
Por ejemplo, dado el axioma "F" y la regla "F=F[+F]F", siendo por ejemplo "F" moverse hacia adelante o "+" rotar un cierto ángulo. En pocas iteraciones el sistema-L generará de forma revursiva una cadena final con un kit de instrucciones complejo:
1: F
2: F[+F]F
3: F[+F]F[+F[+F]F]F[+F]F
4: F[+F]F[+F[+F]F]F[+F]F[+F[+F]F[+F[+F]F]F[+F]F]F[+F]F[+F[+F]F]F[+F]F
Veamos a codificarlo:
class LSystem:
def __init__(self, axiom, rules):
self.axiom = axiom
self.rules = rules
def Generate(self, times):
print(f"===== Generando sistema-L en {times} ciclos =====")
# El valor inicial de las instrucciones es el axioma base
instructions = self.axiom
# Aplicamos las reglas de forma recursiva N repeticiones
for i in range(times):
# Copiamos las instrucciones actuales
previous_instructions = instructions
# Reiniciamos las instrucciones actuales para reprocesarlas
instructions = ""
# Para cada carácter en las instrucciones guardadas
for instruction_char in previous_instructions:
# Si se encuentra definido en las reglas
if instruction_char in self.rules:
# Sumamos la porción substituida de las regglas
instructions += self.rules[instruction_char]
else:
# Sino simplemente sumamos el carácter
instructions += instruction_char
# Debugeamos la regla generada en esa iteración
print("Resultado: ", instructions)
return instructions
Este sistema permite generar la cadena resultante al aplicar las reglas al axioma en un número variable de iteraciones. Debemos pasarle el axioma y un diccionario de reglas y para ejecutarlo el número de repeticiones:
LSystem("F", {"F": "F[+F]F"}).Generate(3)
El resultado de lo anterior es efectivamente la cadena esperada:
===== Generando sistema-L en 3 ciclos =====
Resultado: F[+F]F[+F[+F]F]F[+F]F[+F[+F]F[+F[+F]F]F[+F]F]F[+F]F[+F[+F]F]F[+F]F
Nuestro objetivo ahora es parsear la cadena resultante de manera que la tortuga sepa interpretar cada carácter, cuyos significados serán:
F: Moverse hacia adelante una cantidad determinada.[: Almacenar la posición y rotación actual en una pila.+: Rotar la dirección una cantidad determinada en sentido horario.-: Rotar la dirección una cantidad determinada en sentido antihorario.]: Recuperar la última posición y rotación de la pila.
Podemos añadir un método ExecuteLSystem a nuestra tortuga y procesar desde ahí cada instrucción de la cadena generada:
from copy import copy
class Turtle:
stack = []
@classmethod
def ExecuteLSystem(cls, system, distance, angle):
for instruction in system:
if instruction == 'F':
cls.Forward(distance)
elif instruction == '[':
cls.stack.append((copy(cls.pos), copy(cls.dir)))
elif instruction == '+':
cls.Rotate(angle)
elif instruction == '-':
cls.Rotate(-angle)
elif instruction == ']':
cls.pos, cls.dir = cls.stack.pop()
Importante notar que los valores a añadir en la pila son copias y no los objetos originales. Los objetos se manejan por referencia, debemos copiar los valores para no modificar los originales.
Lo ejecutamos en nuestra aplicación generando al principio el sistema y tendremos nuestro primer fractal generado con un sistema-L:
class OpenGLApp(App):
def Init(self):
self.system = LSystem(
"F", {
"F": "F[+F]F"
}).Generate(5)
def Render(self):
GLUtils.PrepareRender()
Turtle.Reset()
Turtle.ExecuteLSystem(self.system, 10, 90)

Como el resultado se sale de la ventana podemos rectificar las coordenadas (0,0) del espacio ortogonal para centrarlo verticalmente en la base de la ventana:
def Setup(self):
GLUtils.InitOrtho(-300, 300, 0, 600)

Mediante las reglas, la distancia, la rotación y las iteraciones se pueden obtener diferentes fractales:
self.system = LSystem(
"F", {
"F": "F[+F][-F]F"
}).Generate(5)

self.system = LSystem(
"F", {
"F": "FF[+F][--FF][-F+F]"
}).Generate(4)
# Rotación de 25º
Turtle.ExecuteLSystem(self.system, 10, 25)

self.system = LSystem(
"X", {
"F": "FF",
"X": "F+[-F-XF-X][+FF][--XF[+X]][++F-X]"
}).Generate(4)

En la Wikipedia se explica cómo implementar los ejemplos anteriores y muchos más.
Sistemas iterativos de funciones¶
Otra forma de construir fractales es mediante IFSs (Iterated Function Systems). Esencialmente se trata de utilizar una función que a una coordenada le aplica cierta función y devuelve una nueva coordenada, toma la nueva coordenada y le aplica de nuevo la función y así sucesivamente.
Partiremos de un sencillo ejemplo donde en lugar de utilizar la tortuga nos limitaremos a renderizar unos cuantos puntos generados con numpy:
import sys
import math
import numpy as np
import pygame as pg
sys.path.append('..')
from res.App import App
from OpenGL.GL import *
from OpenGL.GLU import *
class Point:
def __init__(self, x=0, y=0):
self.x = x
self.y = y
def __str__(self):
return f"({self.x}, {self.y})"
class GLUtils:
@staticmethod
def InitOrtho(left, right, top, bottom):
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
gluOrtho2D(left, right, top, bottom)
@staticmethod
def PrepareRender():
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
@staticmethod
def DrawPoints(points, size):
glPointSize(size)
glBegin(GL_POINTS)
for point in points:
glVertex2f(point.x, point.y)
glEnd()
class OpenGLApp(App):
def Init(self):
self.points = []
# Generamos 100 puntos de prueba
for _ in range(100):
self.points.append(
Point(np.random.randint(-300, 300),
np.random.randint(0, 400)))
def Setup(self):
GLUtils.InitOrtho(-300, 300, 0, 400)
def Render(self):
GLUtils.PrepareRender()
GLUtils.DrawPoints(self.points, 5)
if __name__ == '__main__':
app = OpenGLApp("OpenGL en Python", 600, 600, 60)
app.Run()

Ahora lo que vamos a hacer es generar un único punto en cada fotograma y su posición vendrá determinado por una serie de condiciones en base a un valor aleatorio. Una vez tengamos el punto calculado lo añadiremos a la lista de puntos y el sistema irá dibujando poco a poco un fractal:
class OpenGLApp(App):
def Init(self):
self.points = []
# Creamos un punto que sirva como origen en cada iteración
self.point = Point()
def Update(self):
# Generamos un número para modificar el punto usando condiciones
r = np.random.rand()
if r < 0.1:
self.point.x = 0.00 * self.point.x + 0.00 * self.point.y + 0.00
self.point.y = 0.00 * self.point.x + 0.16 * self.point.y + 0.00
elif r < 0.86:
self.point.x = 0.85 * self.point.x + 0.04 * self.point.y + 0.00
self.point.y = -0.04 * self.point.x + 0.85 * self.point.y + 1.60
elif r < 0.93:
self.point.x = 0.20 * self.point.x - 0.26 * self.point.y + 0.00
self.point.y = 0.23 * self.point.x + 0.22 * self.point.y + 1.60
else:
self.point.x = -0.15 * self.point.x + 0.28 * self.point.y + 0.00
self.point.y = 0.26 * self.point.x + 0.24 * self.point.y + 0.44
# Añadimos el nuevo punto a la lista
self.points.append(Point(self.point.x, self.point.y))

Fijaros que se ve muy pequeño porque las modificaciones de posisición son también reducidas. Podemos escalar el espacio ortográfico con la función de OpenGL glScaled y estirar el espacio como haciendo un zoom (de paso también cambiaremos el tamaño del punto a 1 píxel):
@staticmethod
def PrepareRender():
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
glScaled(80, 40, 1) # <-----
def Render(self):
GLUtils.PrepareRender()
GLUtils.DrawPoints(self.points, 1) # <-----

El fractal que acabamos de dibujar se llama helecho de Barnsley, fue descrito por el matemático británico Michael Barnsley por primera vez en 1993 y todo el proceso de desarrollo está perfectamente explicado en la Wikipedia. Ahí se detalla como mediante transformaciones se determina la nueva posición de los puntos para 4 grupos en función de una posibilidad: tallo, foliolos sucesivamente más pequeños, foliolo más grande a la izquierda y foliolo más grande a la derecha.
Otro fractal muy famoso que podemos construir es el triángulo de Sierpiński, solo debemos modificar las condiciones así:
def Update(self):
# Generamos un número para modificar el punto usando condiciones
r = np.random.rand()
if r < 0.33:
self.point.x = 0.5 * self.point.x + 0.00 * self.point.y + 0.0
self.point.y = 0.0 *self.point.x + 0.50 * self.point.y + 0.5
elif r < 0.66:
self.point.x = 0.5 * self.point.x + 0.0 * self.point.y + 0.5
self.point.y = 0.0 * self.point.x + 0.5 * self.point.y + 0.0
else:
self.point.x = 0.5 * self.point.x + 0.0 * self.point.y + 0.0
self.point.y = 0.0 * self.point.x + 0.5 * self.point.y + 0.0
# Añadimos el nuevo punto a la lista
self.points.append(Point(self.point.x, self.point.y))

Por defecto se ve muy pequeño, lo podemos escalar y trasladar con OpenGL un poco más arriba:
@staticmethod
def PrepareRender():
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
glTranslate(-300, 0, 0) # <----
glScaled(600, 400, 1) # <----

Por ahora dejamos los fractales, si queréis más información sobre el triángulo de Sierpiński podéis la tenéis en la Wikipedia.
Última edición: 3 de Octubre de 2022
