Dibujando el espacio 3D con OpenGL¶

A partir de ahora vamos a profundizar en cómo funciona el espacio en OpenGL para producir imágenes tridimensionales. Repasaremos las tranformaciones de esenciales, cómo mover la cámara y visualizar la orientación del mundo.

También es un buen momento para dejar por aquí este esquema sobre el pipeline de transformación de los vértices (imagen tomada de este genial artículo de Scratch a pixel):

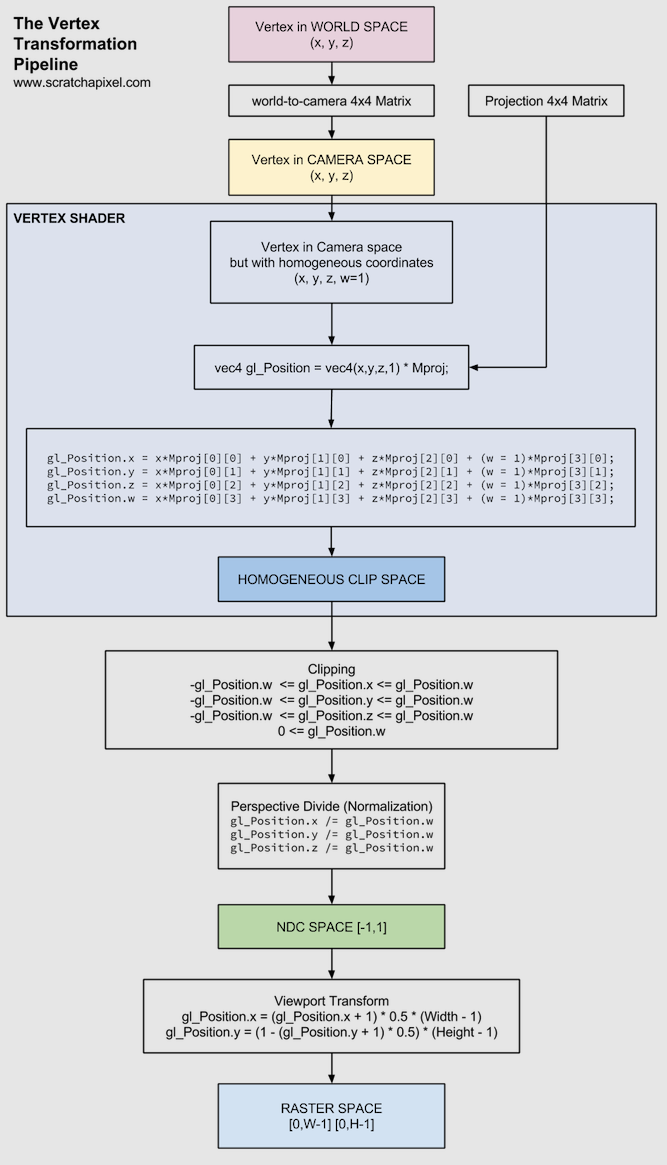
Transformaciones de vista¶

En esta práctica vamos a explorar las view transformations, para ello partiremos de un ejemplo básico cargando el mesh de un cubo sin aplicar ninguna rectificación:

import sys
sys.path.append('..')
from res.App import App
from res.Mesh import *
from OpenGL.GL import *
from OpenGL.GLU import *


class GLUtils:
    @staticmethod
    def InitRender():
        # Projection
        glMatrixMode(GL_PROJECTION)
        glLoadIdentity()
        gluPerspective(60, (600 / 600), 0.1, 500)

    @staticmethod
    def PrepareRender():
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)


class OpenGLApp(App):
    def Init(self):
        GLUtils.InitRender()
        self.mesh = Mesh("../res/models/cube.obj")

    def Render(self):
        GLUtils.PrepareRender()
        self.mesh.Draw()


if __name__ == '__main__':
    app = OpenGLApp("OpenGL en Python", 600, 600, 60)
    app.Run()

Como ya comentamos anteriormente, por defecto la cámara se encuentra el eje Z=0, como el cubo se está dibugando en la matriz de mundo con el centro en el origen (0,0,0), lo que vemos aquí es simplemente la cara del fondo del cubo, pues la cámara está justo sobre esa cara.

Para visualizar el cubo completo debemos aplicarle una transformación de traslación y empujarlo al fondo. Podemos establer el modo modelview, configurar el espacio y activar el bufer de profundidad (si queremos) y configurar la traslación con glTranslate:

class GLUtils:
    @staticmethod
    def InitRender():

        # Projection
        glMatrixMode(GL_PROJECTION)
        glLoadIdentity()
        gluPerspective(60, (600 / 600), 0.1, 500)

        # Model View
        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity()
        glViewport(0, 0, 600, 600)
        glEnable(GL_DEPTH_TEST)
        # Traslación de la cámara del modelo 1 hacia atrás
        glTranslate(0, 0, -2)

Al mover la cámara del modelo -1 unidad del mundo hacia atrás estará exactamente sobre la otra cara, la del frente del cubo:

Si posicionamos la cámara a -2 unidades, la cara frontal del cubo estará a 1 unidad de distancia de la cámara:

glTranslate(0, 0, -2)

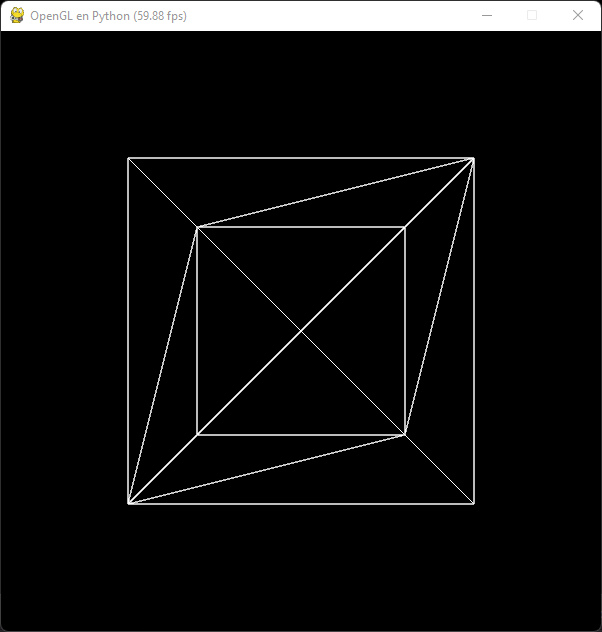
Nota: Debemos recordar que el cubo está normalizado y cada cara mide exactamente 1 unidad del mundo.

En cuanto a los ejes x e y dependen de cómo hemos configurado que crezca el espacio. Por ejemplo, trasladar la cámara del modelo 1 unidad hacia arriba ocasionará que veamos solo la mitad inferior del cubo:

glTranslate(0, 1, -2)

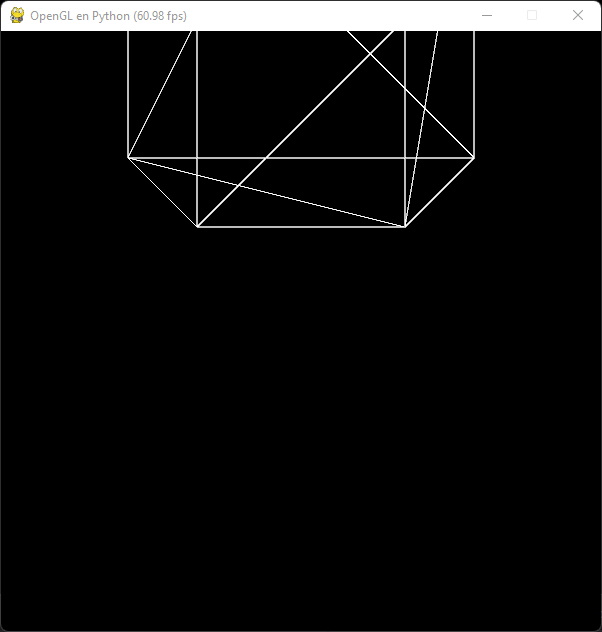
Si en lugar de configurar inicialmente la traslación la establecemos en cada fotograma, ésta se acumulará:

def Render(self):
    GLUtils.PrepareRender()
    glTranslate(0, 0, -1 * self.deltaTime)
    self.mesh.Draw()

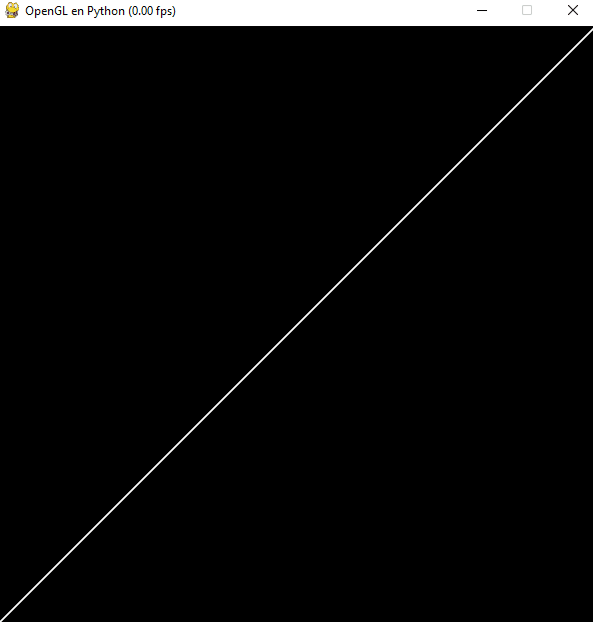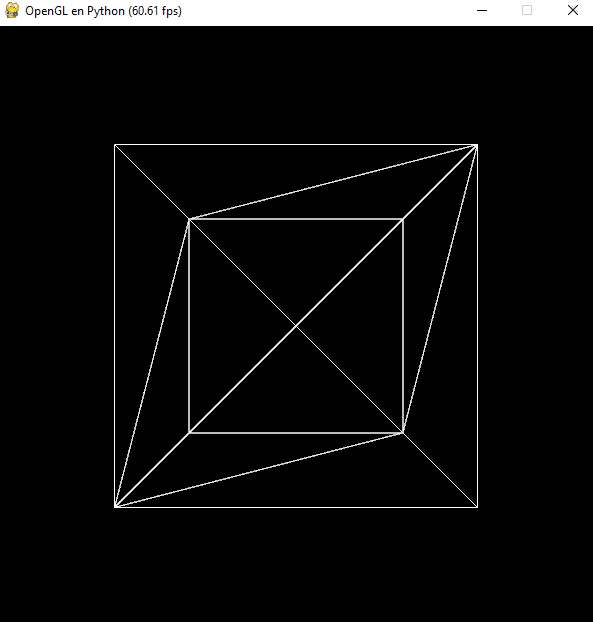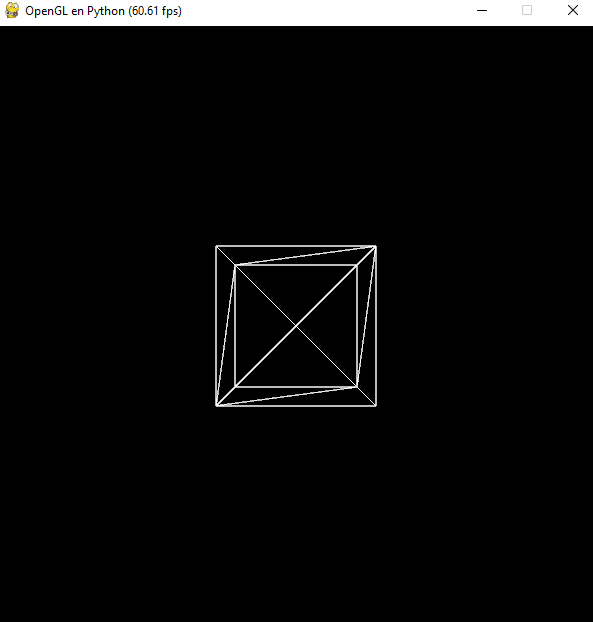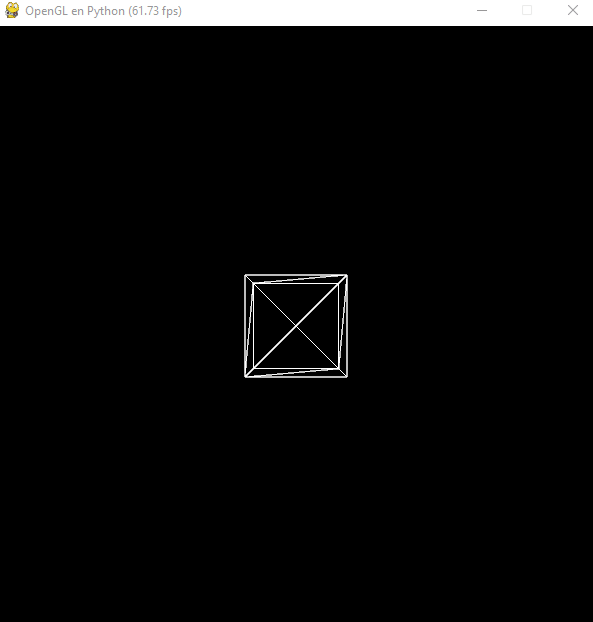
Sin embargo, si utilizamos las instrucciones glPushMatrix y glPopMatrix antes y después de la transformación y el renderizado:

def Render(self):
    GLUtils.PrepareRender()
    glPushMatrix()
    glTranslate(0, 0, -2)
    self.mesh.Draw()
    glPopMatrix()

Podemos insertar la matriz actual en una pila, es decir en la memoria. Metemos las matrices de transformación en la memoria, las ejecutamos y las sacamos de la memoria. Al hacerlo reiniciamos la matriz de la modelview para el próximo fotograma y ya no se acumulan.

Si intentamos dibujar dos cubos, ambos lo harán en la misma posición y no los percibiremos:

def Render(self):
    GLUtils.PrepareRender()
    glPushMatrix()
    glTranslate(0, 1, -2)
    self.mesh.Draw()
    self.mesh.Draw()
    glPopMatrix()

Sin embargo, si reiniciamos cargamos la identidad despueés de dibujar el primer cubo (recordemos que equivale a multipliar por 1):

def Render(self):
    GLUtils.PrepareRender()
    glPushMatrix()
    glTranslate(0, 1, -2)
    self.mesh.Draw()
    glLoadIdentity()
    self.mesh.Draw()
    glPopMatrix()

El segundo cubo se dibujará de nuevo en el origen. Eso ya nos da la pista de que podemos modificar la posición de la subsiguiente malla si primero reiniciamos la transformación con la matriz de identidad:

def Render(self):
    GLUtils.PrepareRender()
    glPushMatrix()
    glTranslate(0, 1, -2)
    self.mesh.Draw()
    glLoadIdentity()
    glTranslate(0, -1, -2)
    self.mesh.Draw()
    glPopMatrix()

Exactamente lo mismo ocurrirá con las transformaciones de escalado y rotación

def Render(self):
    GLUtils.PrepareRender()
    glPushMatrix()

    # Cube 1: Translate - Rotate - Scale
    glTranslate(0, 0.25, -2)
    glRotated(45, 0, 1, 0)
    glScalef(1.25, 0.25, 1)
    self.mesh.Draw()

    glLoadIdentity()

    # Cube 2: Translate - Rotate - Scale
    glTranslate(0, -0.25, -2)
    glRotated(-45, 0, 1, 0)
    glScalef(0.5, 0.25, 1)
    self.mesh.Draw()

    glPopMatrix()

Nota: OpenGL lee las matrices en orden mayor de columna, por lo que las transformaciones deben ser:

Traslación
Rotación
Escalado

Si el sistema utilizase orden mayor de fila, las transformaciones serían en el orden inverso:

Escalado
Rotación
Traslación

Este concepto lo explico más en profundidad en mis apuntes de renderizado 3D.

Moviendo la cámara¶

En esta práctica vamos a crear una clase para gestionar nuestra propia cámara. Vamos a partir del siguiente programa:

import sys
sys.path.append('..')
from res.App import App
from res.Mesh import *
from OpenGL.GL import *
from OpenGL.GLU import *

class OpenGLApp(App):
    def Init(self):
        # Projection
        glMatrixMode(GL_PROJECTION)
        glLoadIdentity()
        gluPerspective(60, (600 / 600), 0.1, 500)
        # Model View
        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity()
        glViewport(0, 0, 600, 600)
        glEnable(GL_DEPTH_TEST)
        # Mesh Loading
        self.mesh = Mesh("../res/models/cube.obj")

    def Render(self):
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
        glPushMatrix()
        self.mesh.Draw()
        glPopMatrix()


if __name__ == '__main__':
    app = OpenGLApp("OpenGL en Python", 600, 600, 60)
    app.Run()

La clase cámara establecerá en cada fotograma la transformación de visualización de OpenGL. Básicamente contaremos con distintos vectores para manejar la posición y mover la cámara:

import pygame as pg
from OpenGL.GLU import *
from math import *

class Camera:
    def __init__(self):
        # Posición del ojo (origen)
        self.eye = pg.math.Vector3(0, 0, 0)
        # Vectores de dirección Y, X, Z
        self.up = pg.math.Vector3(0, 1, 0)
        self.right = pg.math.Vector3(1, 0, 0)
        self.forward = pg.math.Vector3(0, 0, 1)
        # Dirección hacia donde mira la cámara (adelante)
        self.look = self.eye + self.forward

    def Update(self, deltaTime=1):
        keys = pg.key.get_pressed()
        # Si presionamos la letra W moveremos la cámara adelante
        if keys[pg.K_w]:
            self.eye += self.forward * deltaTime
        # Si presionamos la letra S moveremos la cámara atrás
        if keys[pg.K_s]:
            self.eye -= self.forward * deltaTime
        # Si presionamos la letra D moveremos la cámara a la derecha
        if keys[pg.K_d]:
            self.eye += self.right * deltaTime
        # Si presionamos la letra A moveremos la cámara a la izquierda
        if keys[pg.K_a]:
            self.eye -= self.right * deltaTime
        # Actualizamos la dirección a donde mira la cámara
        self.look = self.eye + self.forward
        # Estableceremos la transformación de visualización
        # https://docs.microsoft.com/eu-es/windows/win32/opengl/glulookat
        gluLookAt(self.eye.x, self.eye.y, self.eye.z,
                  self.look.x, self.look.y, self.look.z,
                  self.up.x, self.up.y, self.up.z)

Para usar la clase creamos una instancia de Camera y trasladaremos la configuración del model view junto con la actualización de la cámara a su propio método que llamaremos cada fotograma :

from res.Camera import Camera

class OpenGLApp(App):
    def Init(self):
        # Configure the projection
        glMatrixMode(GL_PROJECTION)
        glLoadIdentity()
        gluPerspective(60, (600 / 600), 0.1, 500)
        # Setup the mesh
        self.mesh = Mesh("../res/models/cube.obj")
        # Setup the camera
        self.camera = Camera()

    def UpdateCamera(self):
        # Model View
        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity()
        glViewport(0, 0, 600, 600)
        glEnable(GL_DEPTH_TEST)
        # Camera Updating
        self.camera.Update(self.deltaTime)

    def Render(self):
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
        self.UpdateCamera()
        glPushMatrix()
        self.mesh.Draw()
        glPopMatrix()

Listo, ya tenemos una cámara que podemos mover en tiempo real con el teclado.

Rotando la cámara¶

Un objeto tridimensional puede rotar a partir de uno de sus tres ejes. El ángulo de rotación recibe un nombre distinto para cada eje:

Pitch para la rotación congelando el eje X.
Yaw para la rotación congelando el eje Y.
Roll para la rotación congelando el eje Z.

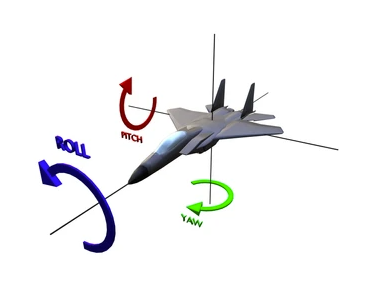
En esta práctica vamos a mapear los ángulos pitch y yaw en función del cursor del ratón para rotar la cámara en el espacio 3D, consiguiendo un efecto similar al de una cámara en primera persona.

Continuando con la cámara en movimiento, vamos a añadirle dos atributos para controlar los ángulos:

self.pitch = 0
self.yaw = 0

Un tercer atributo será un Vector2 para almacenar la última posición del ratón, inicialmente estará justo en el centro de la pantalla:

self.lastMouse = pg.math.Vector2(300, 300)

Durante la actualización de la cámara recuperaremos la posición del ratón y calcularemos la diferencia respecto a la posición anterior:

def Update(self, deltaTime=1):
    mousePos = pg.mouse.get_pos()
    mouseChange = self.lastMouse - pg.math.Vector2(mousePos)
    self.lastMouse = mousePos

Aplicando trigonometría podemos aplicar los nuevos ángulos de rotación en función de la posición del ratón, para mas detalles sobre esto aquí dejo mis apuntes sobre rotación de vectores. Una vez la tenemos aplicada al vector forward, recalculamos los vectores right y up mediante el producto vectorial, siempre normalizados:

def Rotate(self, yaw, pitch):
    # Incrementamos los ángulos de rotación
    self.yaw += yaw
    self.pitch += pitch
    # Aplicamos las rotaciones mediante trigonometría
    self.forward.x = cos(radians(self.yaw)) * cos(radians(self.pitch))
    self.forward.y = sin(radians(self.pitch))
    self.forward.z = sin(radians(self.yaw)) * cos(radians(self.pitch))
    # Normalizamos el vector adelante
    self.forward = self.forward.normalize()
    # Recalculamos el vector derecho haciendo el producto vectorial
    self.right = self.forward.cross(pg.Vector3(0,1,0)).normalize()
    # Recalculamos el vector arriba haciendo el producto vectorial
    self.up = self.right.cross(self.forward).normalize()

Nota: Para evitar un futuro bug deberíamos establecer la posición inicial del vector forward de la misma forma durante el constructor de la clase Camera:

class Camera:
    def __init__(self):
        self.pitch = 0
        self.yaw = 0
        # Valor inicial del vector forward normalizado
        self.forward.x = cos(radians(self.yaw)) * cos(radians(self.pitch))
        self.forward.y = sin(radians(self.pitch))
        self.forward.z = sin(radians(self.yaw)) * cos(radians(self.pitch))
        self.forward = self.forward.normalize()

Ya podremos llamar al método después de actualizar la última posición del ratón:

def Update(self, deltaTime=1):
    mousePos = pg.mouse.get_pos()
    mouseChange = self.lastMouse - pg.math.Vector2(mousePos)
    self.lastMouse = mousePos
    self.Rotate(mouseChange.x, mouseChange.y)

En este punto si queremos que al movernos horizontalmente la rotación sea acorde con el ratón debemos negar el ángulo X, también podemos reducir la sensibilidad del mouse usando un deltaTime por una cantidad de unidades del mundo por segundo:

class Camera:
    def __init__(self):
        self.mouseSensitivity = pg.math.Vector2(10, 15)

    def Update(self, deltaTime=1):
        self.Rotate(
            -mouseChange.x * self.mouseSensitivity.x * deltaTime,
             mouseChange.y * self.mouseSensitivity.y * deltaTime)

Podemos añadir una rectificación al ángulo pitch para establecer un ángulo mínimo y máximo y no permitir una rotación vertical sobre el propio eje X:

def Rotate(self, yaw, pitch):
    # Incrementamos los ángulos de rotación
    self.pitch += pitch
    self.yaw += yaw
    if self.pitch > 89.0: self.pitch = 89
    if self.pitch < -89.0: self.pitch = -89

En este punto si salimos del espacio de la ventana la rotación dejará de funcionar, podemos establecer la configuración de PyGame para que el ratón se quede dentro, además podemos esconderlo:

class OpenGLApp(App):
    def Init(self):
        # Configure Window
        pg.event.set_grab(True)
        pg.mouse.set_visible(False)

Esto implicará que no se pueda clicar el botón de salir, podemos implementar que mediante la tecla ESC se cierre el juego en App:

while 1:
    self.events = pg.event.get()
    for event in self.events:
        if event.type == pg.QUIT:
            sys.exit()
        if event.type == KEYDOWN:
            if event.key == K_ESCAPE:
                sys.exit()

En este punto la cámara funcionará bastante bien:

Lamentablemente seguimos limitados por el espacio de la ventana y no podemos seguir rotando la vista, debemos encontrar una forma de solucionarlo.

Lo que haremos es que la cámara sea consciente del tamaño de la ventana y reinicie la posición del ratón justo al centro después de mover el ratón en cada fotograma. Luego actualizaremos la última posición, pero en lugar de la posición inicial utilizaremos la que hemos establecido en medio de la pantalla:

def UpdateCamera(self):
    # Camera Updating
    self.camera.Update(self.deltaTime, self.screenWidth, self.screenHeight)

def Update(self, deltaTime=1, screenWidth=1, screenHeight=1):
    mousePos = pg.mouse.get_pos()
    mouseChange = self.lastMouse - pg.math.Vector2(mousePos)
    pg.mouse.set_pos(screenWidth/2, screenHeight/2)  # <-----
    self.lastMouse = pg.mouse.get_pos()              # <-----

Ahora ya podemos rotar indefinidamente la cámara:

Solo nos falta encontrar una forma de alternar si queremos mover/rotar la cámara o no. Para mí la mejor forma de hacerlo es cuando el clic derecho del ratón está clicado. Quitaremos que el ratón desaparezca inicialmente y en su lugar detectaremos el clic derecho para activar el modo grab y ratón invisible:

class OpenGLApp(App):
    def Inputs(self):
        for event in self.events:
            if event.type == MOUSEBUTTONDOWN and event.button == 1:
                pg.mouse.set_pos(self.screenWidth / 2, self.screenHeight / 2)
                pg.mouse.set_visible(False)
                pg.event.set_grab(True)
            if event.type == MOUSEBUTTONUP and event.button == 1:
                pg.mouse.set_pos(self.screenWidth / 2, self.screenHeight / 2)
                pg.mouse.set_visible(True)
                pg.event.set_grab(False)

Notar que reiniciaremos la posición al centro de la pantalla antes y después de dejar clicado el botón, eso suavizará la transición entre el modo "movimiento" y el normal.

Simplemente haremos una comprobación a nivel del Camera.Update, inidicándole que sólo actualice la rotación si éste no es visible:

def Update(self, deltaTime=1, screenWidth=1, screenHeight=1):
    if not pg.mouse.get_visible():

        # Procesamiento de la dirección
        mouseChange = self.lastMouse - pg.math.Vector2(pg.mouse.get_pos())
        pg.mouse.set_pos(screenWidth / 2, screenHeight / 2)
        self.Rotate(-mouseChange.x * self.mouseSensitivity.x * deltaTime,
                    mouseChange.y * self.mouseSensitivity.y * deltaTime)
        self.lastMouse = pg.mouse.get_pos()

    # Precesamiento del movimiento
    keys = pg.key.get_pressed()
    # Si presionamos la letra W moveremos la cámara adelante
    if keys[pg.K_w]:
        self.eye += self.forward * deltaTime
    # Si presionamos la letra S moveremos la cámara atrás
    if keys[pg.K_s]:
        self.eye -= self.forward * deltaTime
    # Si presionamos la letra D moveremos la cámara a la derecha
    if keys[pg.K_d]:
        self.eye += self.right * deltaTime
    # Si presionamos la letra A moveremos la cámara a la izquierda
    if keys[pg.K_a]:
        self.eye -= self.right * deltaTime
    # Si presionamos el espacio moveremos la cámara hacia arriba
    if keys[pg.K_SPACE]:
        self.eye += self.up * deltaTime
    # Si presionamos el ALT izquierdo moveremos la cámara abajo
    if keys[pg.K_LALT]:
        self.eye -= self.up * deltaTime

    # Actualizamos la dirección a donde mira la cámara
    self.look = self.eye + self.forward
    # Estableceremos la transformación de visualización
    # https://docs.microsoft.com/eu-es/windows/win32/opengl/glulookat
    gluLookAt(self.eye.x, self.eye.y, self.eye.z,
                self.look.x, self.look.y, self.look.z,
                self.up.x, self.up.y, self.up.z)

El resultado será simplemente perfecto:

Visualizando la orientación¶

En esta práctica vamos a dibujar unas líneas representando el punto de origen del mundo tridimensional y sus vectores con dirección arriba, derecha y adelante.

Utilizaremos como base el programa anterior:

import sys
import pygame as pg
from pygame.locals import *
sys.path.append('..')
from res.App import App
from res.Camera import Camera
from res.Mesh import *
from OpenGL.GL import *
from OpenGL.GLU import *


class OpenGLApp(App):
    def Init(self):
        # Configure the projection
        glMatrixMode(GL_PROJECTION)
        glLoadIdentity()
        gluPerspective(60, (600 / 600), 0.1, 500)
        # Setup the mesh
        self.mesh = Mesh("../res/models/cube.obj")
        # Setup the camera
        self.camera = Camera()

    def Inputs(self):
        for event in self.events:
            if event.type == MOUSEBUTTONDOWN and event.button == 1:
                pg.mouse.set_pos(self.screenWidth / 2, self.screenHeight / 2)
                pg.mouse.set_visible(False)
                pg.event.set_grab(True)
            if event.type == MOUSEBUTTONUP and event.button == 1:
                pg.mouse.set_pos(self.screenWidth / 2, self.screenHeight / 2)
                pg.mouse.set_visible(True)
                pg.event.set_grab(False)

    def UpdateCamera(self):
        # Model View
        glMatrixMode(GL_MODELVIEW)
        glLoadIdentity()
        glViewport(0, 0, 600, 600)
        glEnable(GL_DEPTH_TEST)
        # Camera Updating
        self.camera.Update(self.deltaTime, self.screenWidth, self.screenHeight)

    def Render(self):
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
        self.UpdateCamera()
        glPushMatrix()
        self.mesh.Draw()
        glPopMatrix()


if __name__ == '__main__':
    app = OpenGLApp("OpenGL en Python", 600, 600, 60)
    app.Run()

Empecemos dibujando unas líneas para representar los ejes x, y, z:

class OpenGLApp(App):
    def DrawWorldAxes(self):
        glLineWidth(3)
        glBegin(GL_LINES)
        glVertex3d(-1000, 0, 0) # X Axis
        glVertex3d(1000, 0, 0)
        glVertex3d(0, -1000, 0) # Y Axis
        glVertex3d(0, 1000, 0)
        glVertex3d(0, 0, -1000) # Z Axis
        glVertex3d(0, 0, 1000)
        glEnd()
        glLineWidth(1)

    def Render(self):
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
        self.DrawWorldAxes() # <-----
        self.UpdateCamera()
        glPushMatrix()
        self.mesh.Draw()
        glPopMatrix()

Podemos hacerlas de distintos colores:

def DrawWorldAxes(self):
    glLineWidth(3)
    glBegin(GL_LINES)
    glColor(1, 0, 0)
    glVertex3d(-1000, 0, 0)  # X Axis
    glVertex3d(1000, 0, 0)
    glColor(0, 1, 0)
    glVertex3d(0, -1000, 0)  # Y Axis
    glVertex3d(0, 1000, 0)
    glColor(0, 0, 1)
    glVertex3d(0, 0, -1000)  # Z Axis
    glVertex3d(0, 0, 1000)
    glEnd()
    glColor(1, 1, 1)
    glLineWidth(1)

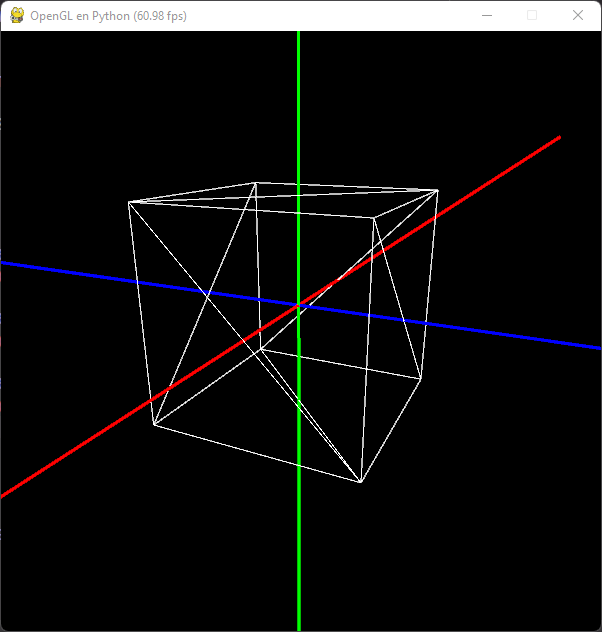
Ahora podemos dibujar en la longitud 1 de cada eje una esfera. Para ello crearemos un objeto cuádrico de OpenGL. De paso modificaremos la longitud de las líneas a una sola unidad:

def DrawWorldAxes(self):

    # Dibujamos las líneas para los ejes
    glLineWidth(3)
    glBegin(GL_LINES)
    glColor(1, 0, 0)
    glVertex3d(-100, 0, 0)  # Eje X
    glVertex3d(100, 0, 0)
    glColor(0, 1, 0)
    glVertex3d(0, -100, 0)  # Eje Y
    glVertex3d(0, 100, 0)
    glColor(0, 0, 1)
    glVertex3d(0, 0, -100)  # Eje Z
    glVertex3d(0, 0, 100)
    glEnd()

    # Creamos un objeto cuádrico en OpenGL para una esfera
    # https://docs.microsoft.com/es-es/windows/win32/opengl/glunewquadric
    sphere = gluNewQuadric()

    # Dibujamos una esfera para el eje X
    glColor(1, 0, 0)
    glPushMatrix()
    glTranslated(1, 0, 0)
    gluSphere(sphere, 0.05, 10, 10)
    glPopMatrix()

    # Dibujamos una esfera para el eje Y
    glColor(0, 1, 0)
    glPushMatrix()
    glTranslated(0, 1, 0)
    gluSphere(sphere, 0.05, 10, 10)
    glPopMatrix()

    # Dibujamos una esfera para el eje Z
    glColor(0, 0, 1)
    glPushMatrix()
    glTranslated(0, 0, 1)
    gluSphere(sphere, 0.05, 10, 10)
    glPopMatrix()

    glColor(1, 1, 1)
    glLineWidth(1)

Si modificamos el ángulo inicial yaw a -90 para alinear la cámara con el origen para el eje x moviéndonos hacia atrás veremos los ejes del cubo en el mundo en el punto de origen:

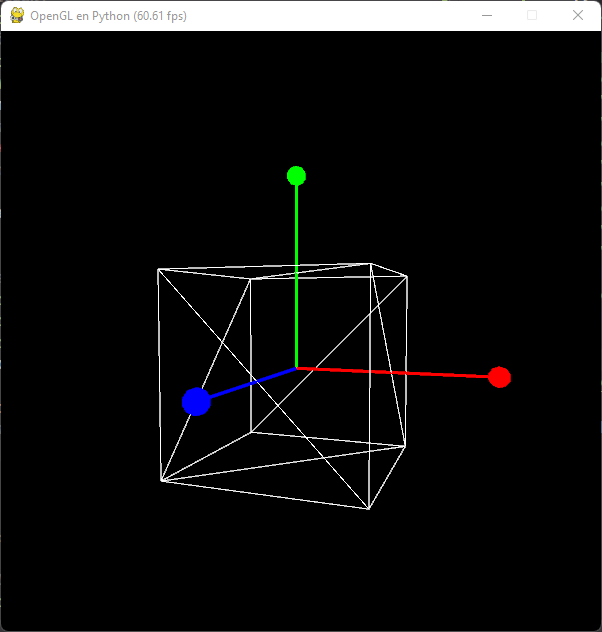
Última edición: 3 de Octubre de 2022