Transformaciones afines con OpenGL¶
En esta sección vamos a repasar las transformaciones afines mediante matrices y su funcionamiento en OpenGL:
- Traslación: Movimiento del objeto a lo largo de los ejes:
glTranslated(x, y, z) # digit
glTranslatef(x, y, z) # float
- Rotación: Orientación del objeto respecto a los ejes. Alrededor del eje
Yse denominayaw, para el ejeXse llamapitchy para el ejeZesrolly se especifica en grados:
glRotated(angle, x, y, z) # digit
glRotatef(angle, x, y, z) # float
- Escalado: Redimensión del objeto respecto a los ejes:
glScaled(x, y, z) # digit
glScalef(x, y, z) # float
- Cizallamiento (shearing): Movimiento parcial alrededor de una o más dimensiones.
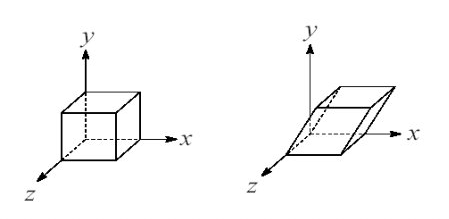
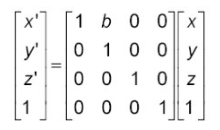
No hay función como tal, la matriz de shearing es la siguiente:
Acerca de las matrices¶
Las matrices son un concepto fundamental en los gráficos por computadora y se utilizan en casi todos los cálculos que involucran mover y ubicar objetos.
Una matriz es un arreglo rectangular de números con una cantidad fija de filas y columnas:
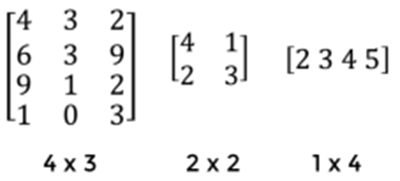
Una matriz con una fila se llama vector de fila y una matriz con una columna se llama vector de columna:

Una matriz cuadrada, que es el tipo más común utilizado en los cálculos de juegos de computadora, es una con el mismo número de filas que columnas:
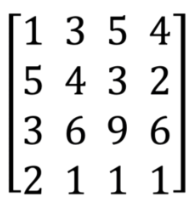
Las matrices cuadradas que se usan con frecuencia son la matriz cero y la matriz de identidad.
Una matriz cero, como su nombre indica, es todo ceros, y una matriz identidad es todo ceros con unos en la diagonal:
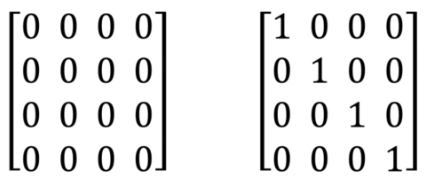
La matriz de identidad se considera la matriz neutra. De forma simular al número 1, multiplicar una matriz por la identidad da como resulta la misma matriz.
Todos los cálculos matemáticos comunes se pueden realizar en matrices.
El escalado, que denota una multiplicación o división, implica multiplicar cada valor de la matriz por un mismo número. Por ejemplo, en esta matriz de dos por dos se multiplica por cuatro la matriz resultante:
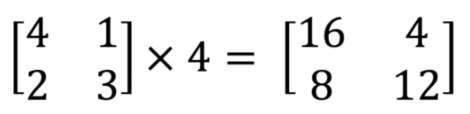
La suma y la resta solo es posible entre los elementos de las mismas posiciones:
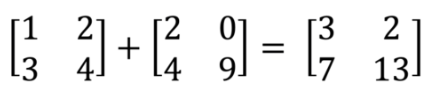
Otro concepto que usamos cuando trabajamos con matrices es el de la matriz transpuesta.
La transposición de una matriz es cuando los valores de las filas se intercambian con los valores de las columnas:
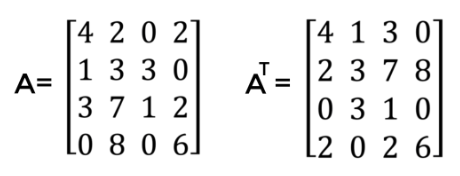
La multiplicación de matrices es el quid de muchas operaciones que ocurren en los gráficos y juegos de computadora.
Dos matrices solo se pueden multiplicar si se pueden formar. Eso significa que el número de columnas de la primera matriz debe ser igual al número de filas en la segunda matriz:
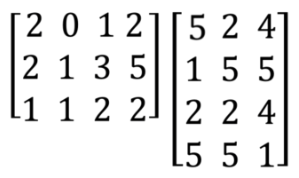
Básicamente, tomamos cada fila de la primera matriz y encontramos el producto escalar de ella y las columnas de la segunda matriz.
La primera fila será:
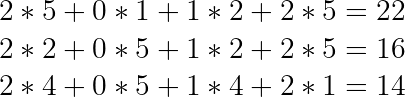
La segunda:
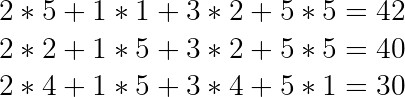
Y la tercera:
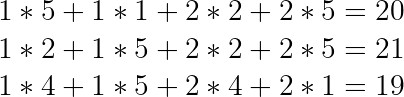
El resultado final, una matriz con el mismo número de filas que la primera y columnas que la segunda:
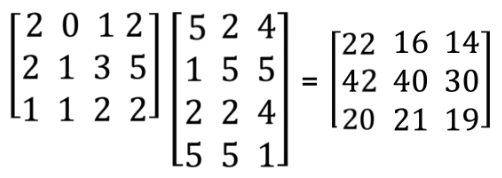
Matrices de transformación¶
El quid de la cuestión es que las transformaciones se pueden traducir a matrices, de manera que al multiplicar las matrices de transformación entre ellas obtenemos una única matriz conocida como matriz de mundo.
En lugar de realizar los cálculos una y otra vez para cada vértice, la matriz de mundo contiene una combinación de todas las demás que dará como resultado el renderizado deseado para cada modelo.
La estructura de la matriz de escalado es la siguiente:
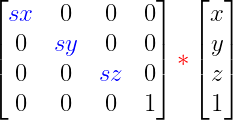
Donde se substituye una matriz de identidad con los factores de escalado en cada componente sx, sy, sz. El resultado es equivalente a multiplicar el punto x,y,z por los factores:
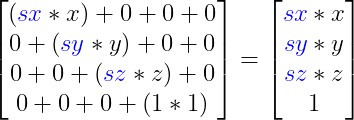
La estructura de la matriz de traslación es la siguiente:
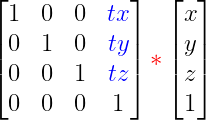
Se trata de una matriz especial, pues realmente lo que necesitamos es sumar la cantidad de traslación tx, ty, tz en cada eje.
La traslación no es una transformación lineal, sino que utiliza una cuarta columna para almacenar las distancias de traslación y sumarlas al punto original x,y,z.
Esta es la razón principal por la que se utiliza una matriz 4x4 y no 3x3 también en las demás transformaciones, en caso contrario no podríamos multiplicarlas entre ellas:
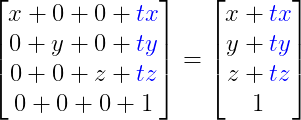
Finalmente la estructura de la matriz de rotación es algo más elaborada, principalmente porque tenemos tres de ellas, una para controlar la rotación en cada eje (yaw, pitch, roll) que podemos conseguir aplicando trigonometría:
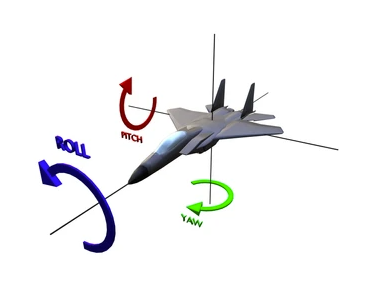
Al congelar el eje X la matriz de rotación para el ángulo pitch es:
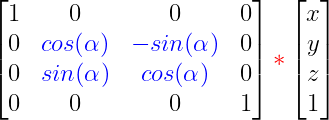
Al congelar el eje Y la matriz de rotación para el ángulo yaw es:
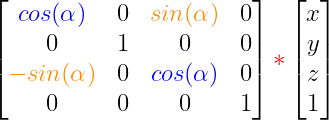
Al congelar el eje Z la matriz de rotación para el ángulo roll es:
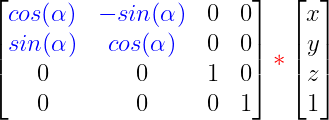
Al multiplicar las tres matrices de rotación entre ellas se consigue la matriz de rotación.
En OpenGL la matriz de mundo es la matriz resultante de multiplicar las tres matrices de transformación por este orden (tal como expliqué anteriormente):
- Traslación
- Rotación
- Escalado
Por suerte no tenemos que multiplicar las matrices a mano, solo tenemos que configurar la cantidad de traslación, rotación y escalado en cada eje y dejar que OpenGL se encargue de realizar los cálculos.
Traslación en nuestra malla¶
Durante las próximas tres prácticas vamos a incorporar las transformaciones afines a nuestra clase Mesh, empezando por la traslación.
import pygame as pg
class Mesh:
def __init__(self, objPath=None, position=pg.Vector3(0, 0, 0),...:
self.position = position
def Draw(self):
glPushMatrix()
glTranslatef(self.position.x, self.position.y, self.position.z)
for i in range(0, len(self.triangles), 3):
glBegin(self.drawtype)
glVertex3fv(self.vertices[self.triangles[i]])
glVertex3fv(self.vertices[self.triangles[i + 1]])
glVertex3fv(self.vertices[self.triangles[i + 2]])
glEnd()
glPopMatrix()
Podemos configurarle la posición inicial:
class OpenGLApp(App):
def Init(self):
# Setup the mesh
self.mesh = Mesh("../res/models/cube.obj", pg.Vector3(1, 1, 1))
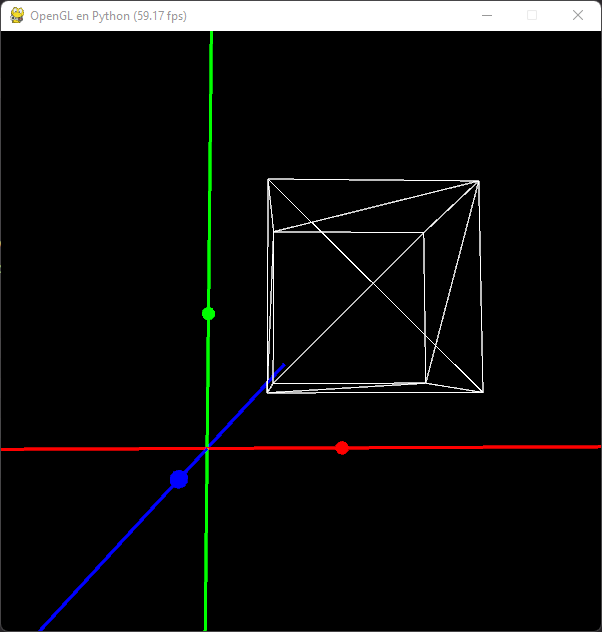
Podríamos dibujar varios cubos uno sobre otro:
class OpenGLApp(App):
def Init(self):
# Setup the meshes
self.meshes = [
Mesh("../res/models/cube.obj", pg.Vector3(0.5, 0.5, -0.5)),
Mesh("../res/models/cube.obj", pg.Vector3(0.5, 1.5, -0.5)),
Mesh("../res/models/cube.obj", pg.Vector3(0.5, 2.5, -0.5))]
def Render(self):
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
self.DrawWorldAxes()
self.UpdateCamera()
for mesh in self.meshes:
mesh.Draw()
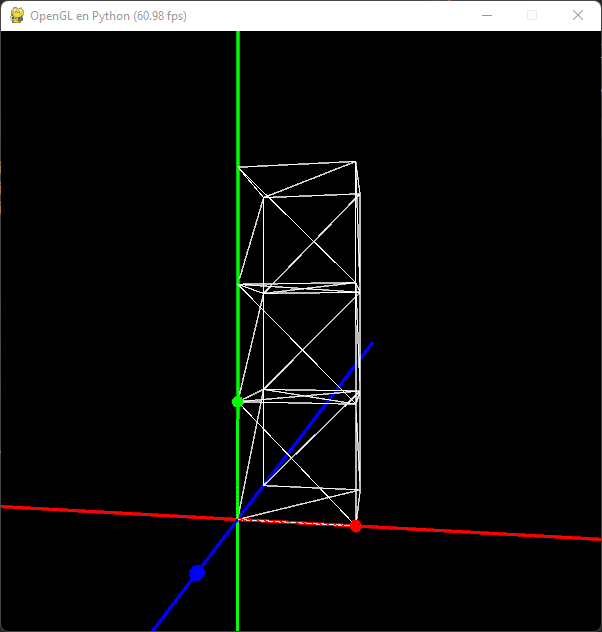
En este punto estamos creando tres objetos independientes uno encima del otro, sin embargo, ya que son el mismo objeto, sería más práctico y óptimo si trasladamos un único cubo y lo dibujamos en tres lugares distintos.
Lo que haremos es enviar al propio método Draw una posición de movimiento relativo donde queramos dibujar el objeto:
def Draw(self, move=pg.Vector3(0, 0, 0)):
glPushMatrix()
glTranslatef(self.position.x, self.position.y, self.position.z)
glTranslatef(move.x, move.y, move.z) # Movimiento relativo
Ahora simplemente con un cubo podemos reposicionarlo de forma relativa antes de dibujarlo tres veces:
class OpenGLApp(App):
def Init(self):
# Setup the mesh
self.mesh = Mesh("../res/models/cube.obj")
def Render(self):
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
self.DrawWorldAxes()
self.UpdateCamera()
self.mesh.Draw(pg.Vector3(0.5, 0.5, -0.5))
self.mesh.Draw(pg.Vector3(0.5, 1.5, -0.5))
self.mesh.Draw(pg.Vector3(0.5, 2.5, -0.5))
Esto es mucho más óptimo, pues se trata del mismo objeto dibujado en diferentes lugares, ocupando en la memoria un solo objeto.
Nada nos impediría utilizar un bucle y dibujar el cubo en forma de tabla 5x5 creando una pared:
def Render(self):
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
self.DrawWorldAxes()
self.UpdateCamera()
for y in range(5):
for x in range(5):
self.mesh.Draw(pg.Vector3(0.5 + x, 0.5 + y, -0.5))
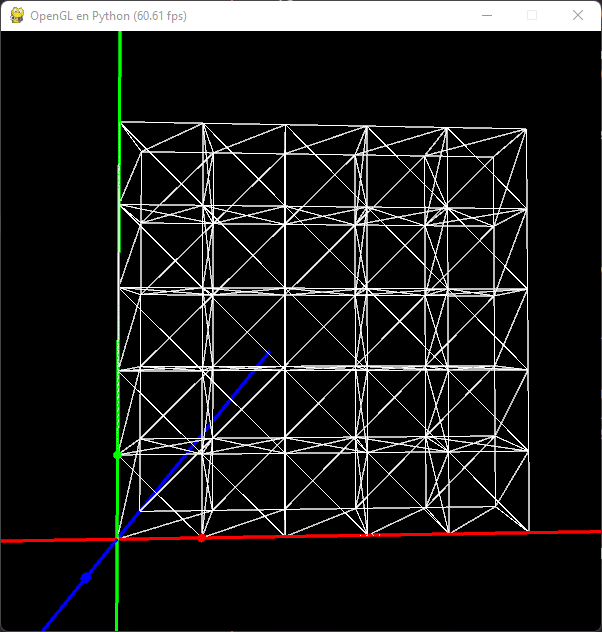
Rotación en nuestra malla¶
A continuación vamos a hacer lo mismo que con la traslación pero implementando la rotación en la clase.
Recordemos que la rotación debe realizarse después de la traslación y antes del escalado, además toma el ángulo y los componentes donde aplicar la rotación, por eso es buena idea crear una clase Rotation con el ángulo y los componentes:
class Rotation:
# Establecemos el ángulo y rotación por defecto a cero
def __init__(self, angle=0, axis=pg.Vector3(0, 0, 0)):
self.angle = angle
self.axis = axis
class Mesh:
def __init__(self, objPath=None, position=pg.Vector3(0, 0, 0), rotation=Rotation(), ...):
self.position = position
self.rotation = rotation
def Draw(self, move=pg.Vector3(0, 0, 0), rotate=Rotation()):
glPushMatrix()
# Procesamos la posición inicial
glTranslatef(self.position.x, self.position.y, self.position.z)
# Sumamos el movimiento relativa
glTranslatef(move.x, move.y, move.z)
# Realizamos la rotación inicial
glRotatef(rotate.angle, self.rotation.axis.x,
self.rotation.axis.y, self.rotation.axis.z)
# Sumamos la rotación relativa
glRotatef(rotate.angle, rotate.axis.x,
rotate.axis.y, rotate.axis.z)
Podemos establecerlo:
class OpenGLApp(App):
def Init(self):
# Setup the meshes
self.mesh = Mesh("../res/models/cube.obj")
def Render(self):
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
self.DrawWorldAxes()
self.UpdateCamera()
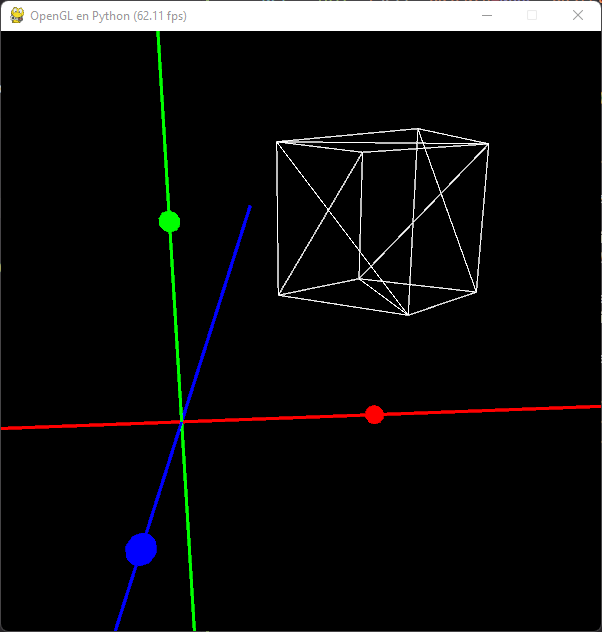
# Dibujamos el modelo con traslación y rotación relativa
self.mesh.Draw(pg.Vector3(1, 1, 0), Rotation(45, pg.Vector3(0, 1, 0)))
Escalado en nuestra malla¶
Por último vamos a añadir el escalado a la clase, como siempre tanto de forma inicial como relativa, después de la rotación:
class Mesh:
def __init__(self, objPath=None, position=pg.Vector3(0, 0, 0), rotation=Rotation(), scaling=pg.Vector3(1, 1, 1), ...):
self.position = position
self.rotation = rotation
self.scaling = scaling
def Draw(self, move=pg.Vector3(0, 0, 0), rotate=Rotation(), scale=pg.Vector3(1, 1, 1)):
glPushMatrix()
# Procesamos la posición inicial
glTranslatef(self.position.x, self.position.y, self.position.z)
# Sumamos el movimiento relativa
glTranslatef(move.x, move.y, move.z)
# Realizamos la rotación inicial
glRotatef(rotate.angle, self.rotation.axis.x,
self.rotation.axis.y, self.rotation.axis.z)
# Sumamos la rotación relativa
glRotatef(rotate.angle, rotate.axis.x,
rotate.axis.y, rotate.axis.z)
# Realizamos el escalado inicial
glScalef(self.scaling.x, self.scaling.y, self.scaling.z)
# Realizamos el escalado relativo
glScalef(scale.x, scale.y, scale.z)
Podemos probar si funciona triplicando el tamaño del cubo ya posicionado y rotado.
def Render(self):
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
self.DrawWorldAxes()
self.UpdateCamera()
# Dibujamos el modelo con traslación, rotación y escalado relativo
self.mesh.Draw(pg.Vector3(1, 1, 0),
Rotation(45, pg.Vector3(0, 1, 0)),
pg.Vector3(3, 3, 3))
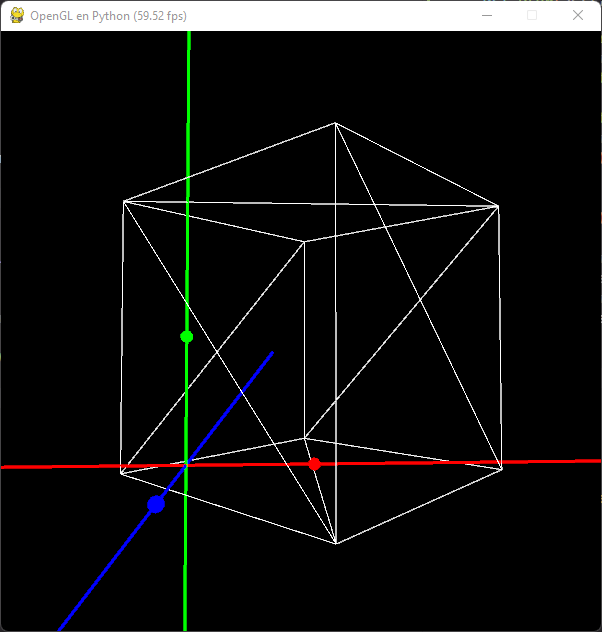
Evidentemente el escalado se realiza respecto al centro del modelo.
Propiedades afines¶
Finalmente comentemos algunas propiedades de estas transformaciones:
- Las líneas se mantienen rectas, los planos se mantienen planos.
- Tanto las líneas como los planos mantienen su paralelisimo.
- Las columnas de la matriz de transformación revelan el sistema de coordenadas.
- Las proporciones de la transformación de escalado se mantienen relativas.
Próximos pasos¶
A partir de este punto la idea es adaptar el código para utilizar shaders, esto nos permitirá entre otras cosas almacenar los vértices en la memoria de la gráfica para ahorrarle a la CPU todo su manejo en cada iteración del bucle, lo cuál aumentará exponencialmente el rendimiento de renderizado y por tanto la cantidad de modelos que podemos dibujar a la vez, pero eso es una historia para otro día...
Última edición: 3 de Octubre de 2022
