Proyección de puntos¶

Las técnicas de proyección nos permiten representar, mediante operaciones matemáticas una dimensión 3D en forma 2D.

Existen varios tipos de proyecciones dependiendo del resultado que nos interese.

Proyección ortográfica¶

Esta proyección es una proyección paralela que consiste en ignorar la profundidad (eje Z).

Para implementar esta proyección en una función recibiremos un vector 3D y devolveremos un vector 2D con únicamente sus componentes X e Y:

Vector2 OrtoraphicProjection(Vector3 p)
{
    return Vector2{p.x, p.y};
}

Para probar la función vamos a crear un cubo de puntos proyectos en 2D. Podemos definir el arreglo fuera del while:

Vector2 cubeProjectedPoints[9 * 9 * 9];

Entre Update y Render proyectamos los puntos a 2D:

window.Update();

// Vector 3D proyectado ortográficamente
for (int i = 0; i < 9 * 9 * 9; i++)
{
    // Proyeccion del punto
    cubeProjectedPoints[i] = OrtoraphicProjection(cubePoints[i]);
}

window.Render();

Ahora durante el renderizado, podemos hacer uso de nuestro método DrawPixel y establecer todos los píxeles del cubo proyectado en el ColorBuffer:

window.Render();
window.DrawGrid(0xFF616161);

/* Dibujar proyección */
for (int i = 0; i < 9 * 9 * 9; i++)
{
    window.DrawPixel(
        cubeProjectedPoints[i].x,
        cubeProjectedPoints[i].y,
        0xFF00FFFF);
}

window.PostRender();

El resultado será el siguiente:

Un pequeño píxel en la parte superior izquierda.

¿Por qué? Pues debido a que los valores de nuestro cubo se encuentran normalizados entre -1 y 1 con el origen en 0.

Esto nos lleva a la idea de que debemos escalar de alguna forma los valores del cubo.

Este escalar se denomina**FOV** (campo de visión) y podemos probar alguna cantidad hasta dar con la que nos guste y mulitiplicarla en nuestra función de proyección:

float fovFactor = 100;

Vector2 OrtoraphicProjection(Vector3 p)
{
    return Vector2{
        fovFactor * p.x, 
        fovFactor * p.y};
}

El resultado por ahora será algo así:

Debemos tener en cuenta que como consecuencia de aplicar el fovFactor, el cubo crece en tamaño y para dibujarlo completamente necesitamos más espacio. Por eso deberemos reposicionarlo, idealmente hacia el centro de la pantalla, tomando su origen (0, 0) como el punto (windowWidth/2, windowHeight/2).

Así que simplemente sumamos esa distancia en sus componentes durante el renderizado:

/* Dibujar proyección reposicionada al centro */
for (int i = 0; i < 9 * 9 * 9; i++)
{
    window.DrawPixel(
        cubeProjectedPoints[i].x + window.windowWidth / 2,
        cubeProjectedPoints[i].y + window.windowHeight / 2,
        0xFF00FFFF);
}

Y ya está, ahora sí con su aspecto real en paralelo:

Proyección perspectiva¶

La proyección en perspectiva consiste en simular la forma en cómo los humanos vemos el mundo, donde los objetos cerca nuestro se perciben mayores que los que están lejos.

Esto introduce la idea de que necesitamos una especie de espectador u ojo como origen de la vista tridimensional con un ángulo de visión que definirá el campo visible, llamado AOV (angle of view).

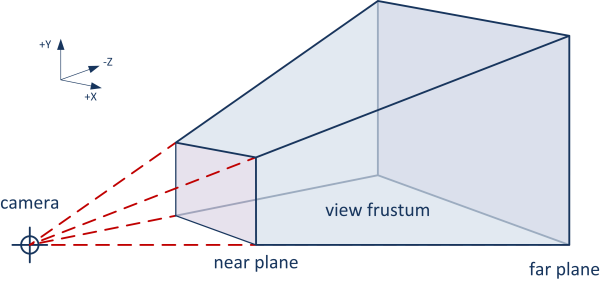
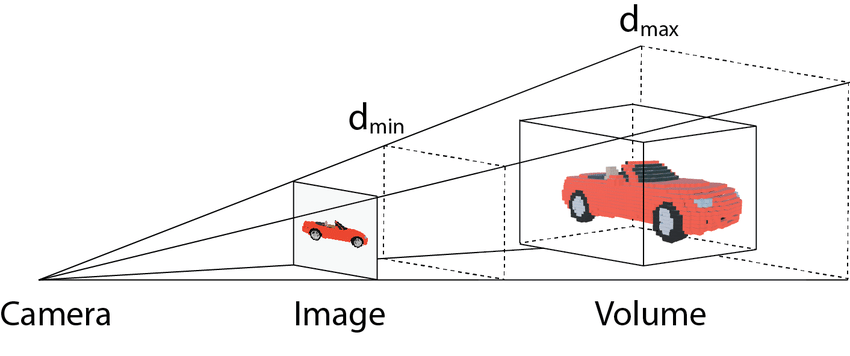
En un videojuego o simulación tridimensional, el origen de la vista es la cámara que nos permite percibir el mundo, abarcando el espacio entre el plano más cercano y el plano más alejado, denominado View Frustum:

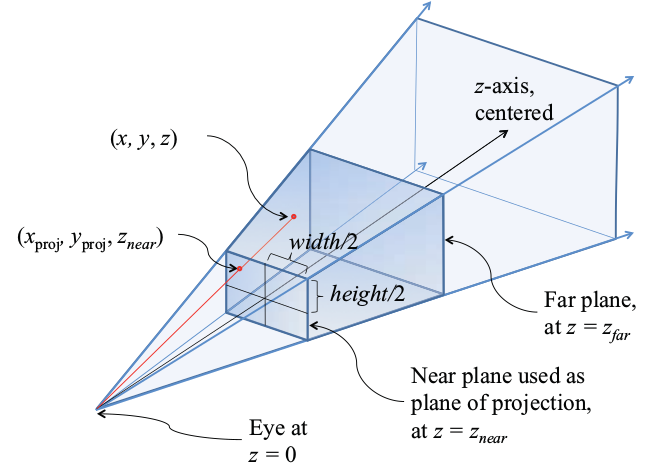
Mediante el uso de la geometría y la propiedad de los triángulos similares de compartir proporciones equivalentes, podemos calcular las fórmulas para los puntos proyectados P'x y P'y:

$\frac{P'x}{Px}=\frac{1}{Pz}\to\frac{Px}{Pz}$

$\frac{P'y}{Py}=\frac{1}{Pz}\to\frac{Py}{Pz}$

Ambas fórmulas se conocen como brechas de perspectiva, en inglés perspective divide y dictan que:

Cuanto menor sea la profundidad z, mayor serán x e y, de manera que los objetos se percibirán más grandes.
Cuanto mayor sea la profundidad z, menores serán x e y, de manera que los objetos se percibirán más pequeños.

Nuestra nueva función de perspectiva simplemente dividirá x e y entre z:

Vector2 PerspectiveProjection(Vector3 p)
{
    return Vector2{
        (fovFactor * p.x) / p.z, 
        (fovFactor * p.y) / p.z};
}

cubeProjectedPoints[i] = PerspectiveProjection(cubePoints[i]);

EL resultado se verá más o menos así:

No es exactamente lo que se espera pero se percibe una especie de profundidad.

La razón por la que se ve de esta forma es que estamos suponiendo que el ojo, el origen de la vista, concuerda justo en la cara más profunda del cubo.

Para solucionarlo debemos alejar nuestra vista del cubo, esto lo conseguiremos restando una profundidad extra mediante un Vector3 para simular la posición de una cámara alejada del fondo del cubo:

Vector3 cameraPosition{0, 0, -5};

Esta distancia la vamos a restar del punto antes de realizar la proyección de perspectiva:

window.Update();

for (int i = 0; i < 9 * 9 * 9; i++)
{
    // Restamos la distancia de la cámara
    Vector3 point = cubePoints[i];
    point.z -= cameraPosition.z;
    // Proyeccion del punto
    cubeProjectedPoints[i] = PerspectiveProjection(point);
}

window.Render();

Si visualizamos el cubo lo visualizaremos muy pequeño pero ya se podrá apreciar la perspectiva:

Podemos rectificar el tamaño mediante la profundidad de la cámara cameraPosition.z o con el factor de escalado del punto de vista fovFactor, probemos cambiando éste último:

float fovFactor = 200;

Al aumentar el factor de escalado el cubo se percibe más grande:

Estos valores no son casuales, todo esto tiene una explicación matemática clara.

Dado que el lado del cubo mide 2 unidades uniformes (de -1 a 1), un factor de 200 ocasionará que el cubo tenga un tamaño de -200 a 200 píxeles al escalarlo, por lo que lado completo medirá 400px.

Ahora bien, como la cámara está a 5 unidades de distancia, podemos suponer que el tamaño que percibiremos será 400/5 = 80px... ¿O no? Pues no, el tamaño del costado es exactamente 100px:

¿Recordáis que al dibujar el cubo lo hacemos desde su cara más profunda?

Considerando eso debemos suponer que para dibujar su cara más cercana debemos alejarnos de la cara profunda exactamente lo que mide el costado del cubo, es decir 2 unidades (200 * 2 px):

Vector3 cameraPosition{0, 0, -2};

Si nuestra suposición es correcta, desde esta posición de la cámara el costado tendrá un tamaño exacto de 400px:

Regla de la mano¶

En nuestro entorno tridimensional hemos asumido algo importante sin darnos cuenta, me refiero a la dirección de crecimiento para la profundidad en el eje Z.

Hemos considerado que cuanto mayor sea la Z más profundidad y cuanto menor sea, menos profundidad. Precisamente por eso le restamos al eje Z de la cámara (0,0,-5), para alejarla del cubo.

Sin embargo sistemas como OpenGL se basan en lo contrario, cuanto mayor sea la Z menos profundidad y cuanto menor sea, más profundidad. En ese sistema para alejar la cámara deberíamos sumar (0,0,5) al eje Z :

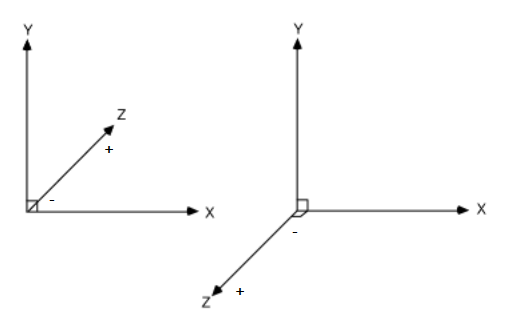
La dirección de la profundidad es un tema importante en la programación gráfica, la forma de realizar algunos cálculos es distinta dependiendo del sistema elegido.

Si ponemos el pulgar de la mano derecha mirando hacia la derecha simulando el eje X y el índice hacia arriba simulando el eje Y, el dedo corazón apuntará hacia nosotros, diremos que la profundidad Z crece hacia fuera de la pantalla. Pero si repetimos el proceso con la mano izquierda, el dedo corazón apuntará al lado inverso, la profundidad Z crece hacia la pantalla:

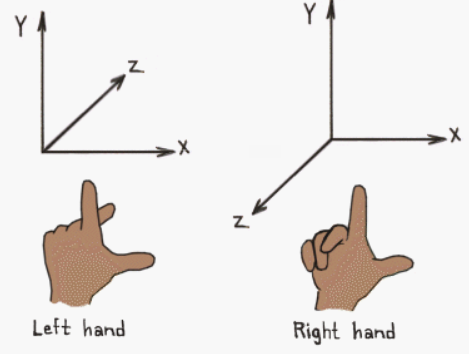
Esto se conoce como regla de la mano y nos permite determinar sentidos vectoriales. Nuestro sistema, al igual que DirectX, se basa en la mano izquierda (la profundidad crece hacia afuera de la pantalla), mientras que OpenGL se basa en la mano izquierda, (la profundidad crece hacia adentro de la pantalla).

Recordar esta sencilla regla nos servirá para más adelante.

Última edición: 05 de Junio de 2022