Transformaciones lineales¶

Hemos visto como dividiendo entre el eje Z hemos conseguido la brecha de perspectiva para la proyección en perspectiva. Sin embargo, esta función es solo uno de los diferentes pasos que necesitamos para conseguir la verdadera proyección en perspectiva.

A parte de dvidir entre Z necesitamos considerar por ejemplo, cuál es ángulo del FOV (el campo de visión) que estamos utilizando, o también el AR (la relación de aspecto) de la pantalla. Para conseguir esto necesitaremos acudir a la proyección de matrices, pero es un tema que trataremos más adelante.

Por ahora utilizaremos la brecha de perspectiva y nos centraremos en algo más interesante, añadir dinamismo a nuestro cubo mediante la aplicación de transformaciones en sus vectores.

Transformando vectores¶

Para transformar los vectores necesitamos acudir al álgebra lineal, la rama de la matemática que estudia las ecuaciones y funciones lineales, así cómo su representación como vectores y matrices.

Las tres transformaciones esenciales son:

Escalado: Para hacer más grande o más pequeño el vector.
Traslación: Para mover el vector de sitio a otro.
Rotación: Para rotar el vector una cierta cantidad.

Las transformaciones las llevaremos a cabo antes de la proyección, durante el evento de actualización y antes del renderizado:

ProcessInput()
Update()
1. TransformPoints()
  1. Rotate(x, y, z)
  2. Scale(amout)
  3. Translate(amout)
2. ProjectPoints()
Render()

Razones trigonométricas¶

Para realizar las transformaciones de los vectores es necesario utilizar la trigonometría, así que vamos a repasar los conceptos básicos.

Trigonometría significa estudio de los trígonos, polígonos con tres lados y tres ángulos.

Las razones trigonométricas son las relaciones entre los lados de un triángulo rectángulo:

$sin(\alpha) = \frac{opuesto}{hipotenusa} \rightarrow s = o / h$

$cos(\alpha) = \frac{adyacente}{hipotenusa} \rightarrow c = a / h$

$tan(\alpha) = \frac{opuesto}{adyacente} \rightarrow t = o / a$

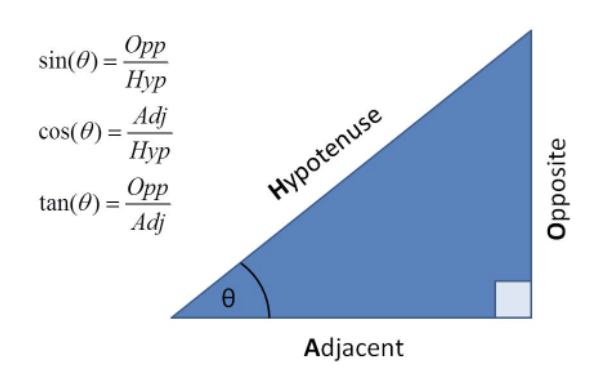
Estas relaciones nos permitirán realizar distintos cálculos esenciales para las transformaciones lineales como por ejemplo la rotación.

Una forma de recordarlas es mediante la palabra sohcahtoa.

Rotación de vectores¶

Ahora que hemos repasado el tema de las razones trignométricas podemos aplicar esos conceptos para rotar los vectores de nuestro cubo.

Para rotar un vector (x,y) se debe aplicar la fórmula de la rotación de matrices:

$\begin{bmatrix}cos (\alpha) & -sin(\alpha)\\sin(\alpha) & cos(\alpha)\\\end{bmatrix} *\begin{bmatrix}x \\y \\\end{bmatrix}$

Dado un vector (x, y) queremos aplicarle una rotación (ángulo) para conseguir el nuevo vector rotado (x', y').

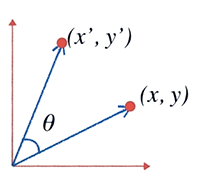
Tomando el triángulo que forma (x, y) con ángulo β y el triángulo que forma (x', y') con ángulo θ podemos establecer sus relaciones trigonométricas para encontrar los valores del vector rotado (x', y'):

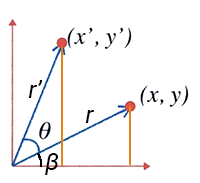
$\\cos( \theta ) = x/r \to x = r * cos(\theta)\\sin( \theta ) = y/r \to y = r * sin(\theta)$

Para determinar los valores rotados necesitamos asumirlos como la suma de θ y β:

$\\cos( \theta + \beta ) = x'/r \to x' = r' * cos(\theta + \beta)\\sin( \theta + \beta) = y'/r \to y' = r' * sin(\theta + \beta)$

No sabemos el ángulo β pero en trigonometría existen las conocidas fórmulas de adición que explican como expandir el seno y el coseno de una suma o resta de dos ángulos:

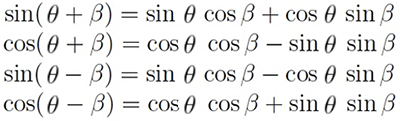
Aplicando la fórmula de adición del ángulo para el coseno:

$\\x' = rcos(\theta + \beta)\\x' = r(cos\theta cos \beta - sin\theta sin\beta)\\x' = rcos\theta cos \beta - rsin\theta sin\beta$

Aquí podemos substituir rcosθ por xy rsinθ por y para conseguir finalmente el valor de x':

$x' = x cos \beta - y sin\beta$

Lo mismo podemos formular para conseguir el valor de y':

$\\ y' = rsin(\theta + \beta)\\ y' = r(sin\theta cos \beta + cos \theta sin \beta)\\ y' = rsin \theta cos \beta + rcos \theta sin \beta\\$

Substituimos rsinθ por y y rcosθ por x para conseguir el valor de y':

$\\ y' = y cos\beta + x sin \beta$

Y ya tenemos las ecuaciones que podemos escribir en forma matricial para un ángulo α:

$\begin{bmatrix}cos (\alpha) & -sin(\alpha)\\sin(\alpha) & cos(\alpha)\\\end{bmatrix} *\begin{bmatrix}x \\y \\\end{bmatrix}$

Ahora bien, esto es para rotar un vector 2D, ¿cómo se aplica con un vector 3D?

Pues si nos lo paramos a pensar, podemos rotar un elemento en base a cualquier de los dimensiones. No es lo mismo rotar algo horizontalmente, que verticalmente o en profundidad.

Al tener tres tipos de rotación el eje aldedor del que vamos a rotar quedará congelado, es decir, no se modificará y es precisamente gracias a eso que no necesitamos nada más para manejar las rotaciones.

Para rotar alrededor del eje z:

$\\ x' = xcos \beta - y sin \beta\\ y' = xsin\beta + ycos\beta\\ z' = inmutable$

Para rotar alrededor del eje y:

$\\ x' = xcos \beta - z sin \beta\\ y' = inmutable\\ z' = xsin\beta+zcos\beta$

Para rotar alrededor del eje x:

$\\ x' = inmutable\\ y' = ycos \beta - z sin \beta\\ z' = ysin\beta+zcos\beta$

Función de rotación¶

Después de tanta trigonometría es hora de programar un poco y llevar a código todo lo que hemos aprendido.

Empecemos creando unos métodos para rotar los vectores 3D:

class Vector3
{
public:
    double x;
    double y;
    double z;

    friend std::ostream &operator<<(std::ostream &os, const Vector3 &v);

    void RotateX(float angle);
    void RotateY(float angle);
    void RotateZ(float angle);
};

La implementación siguiendo las fórmulas de la lección anterior:

void Vector3::RotateX(float angle)
{
    double newY = y * cos(angle) - z * sin(angle);
    double newZ = y * sin(angle) + z * cos(angle);

    y = newY;
    z = newZ;
}
void Vector3::RotateY(float angle)
{
    double newX = x * cos(angle) - z * sin(angle);
    double newZ = x * sin(angle) + z * cos(angle);

    x = newX;
    z = newZ;
}
void Vector3::RotateZ(float angle)
{
    double newX = x * cos(angle) - y * sin(angle);
    double newY = x * sin(angle) + y * cos(angle);

    x = newX;
    y = newY;
}

Ahora, podemos aplicar la rotación a partir de un Vector3 cubeRotation declarado fuera del while:

// Rotación cubo
Vector3 cubeRotation;

Justo antes de proyectar el cubo a 2D, le aplicaremos las transformaciones:

window.Update();

// Rotation transformations per frame
cubeRotation.x += 0.01;
cubeRotation.y += 0.01;
cubeRotation.z += 0.01;

for (size_t i = 0; i < 9 * 9 * 9; i++)
{
    Vector3 point = cubePoints[i];
    // Rotation transformations
    point.RotateX(cubeRotation.x);
    point.RotateY(cubeRotation.y);
    point.RotateZ(cubeRotation.z);
    // Restamos la distancia de la cámara
    point.z -= cameraPosition.z;
    // Proyeccion del punto
    cubeProjectedPoints[i] = PerspectiveProjection(point);
}

window.Render();

Como resultado tendremos el cubo rotando:

Refactorización 2¶

Tenemos mucho que refactorizar en la ventana y nuestros vectores, así que pongámonos manos a la obra.

Empezando por las variables del fovFactor y el cameraPosition dentro de la ventana como variables públicas, eso nos permitirá luego, a través de un puntero de window, acceder desde cualquier lugar a ellos.

#include "vector.h"

class Window
{
public:
    float fovFactor = 400;
    Vector3 cameraPosition{0, 0, -5};

A continuación los métodos de proyección podemos incluirlos en nuestros vectores de manera que un Vector3 devuelva ya su versión Vector2 proyectada a partir de un fovFactor:

class Vector3
{
public:
    Vector2 OrtoraphicProjection(float fovFactor);
    Vector2 PerspectiveProjection(float fovFactor);
};

La implementación quedaría así:

Vector2 Vector3::OrtoraphicProjection(float fovFactor)
{
    return Vector2{fovFactor * x, fovFactor * y};
}

Vector2 Vector3::PerspectiveProjection(float fovFactor)
{
    return Vector2{(fovFactor * x) / z, (fovFactor * y) / z};
}

Para utilizarlos simplemente cambiaremos:

// cubeProjectedPoints[i] = PerspectiveProjection(point);
cubeProjectedPoints[i] = point.PerspectiveProjection(fovFactor);

También refactorizaremos los tres métodos de rotar X, Y, Z en un único método que tome un Vector3 para las cantidades y el ángulo:

void Rotate(Vector3 angles);

La implementación se ejecutará en función de los valores del Vector de cantidades

void Vector3::Rotate(Vector3 angles)
{
    if (angles.x != 0)
        RotateX(angles.x);
    if (angles.y != 0)
        RotateY(angles.y);
    if (angles.z != 0)
        RotateZ(angles.z);
}

Llamarlo será tan sencillo como:

// Rotation transformations
point.Rotate(cubeRotation);

En este punto lo más interesante sería crear nuestra propia clase cube para crear y renderizar cubos de forma sencilla, además nos permitirá separar cómodamente la función principal de los objetos tridimensionales:

#ifndef CUBE_H
#define CUBE_H

#include <iostream>
#include <memory>
#include "vector.h"

// Para prevenir dependencias cíclicas
class Window;

class Cube
{
public:
    size_t pointsCounter{0};
    std::unique_ptr<Vector2[]> projectedPoints;

private:
    Window *window;
    Vector3 rotation;
    Vector3 rotationAmount;
    std::unique_ptr<Vector3[]> points;

public:
    Cube() = default;
    Cube(Window *window, int length);
    void SetRotationAmount(float x, float y, float z);
    void Update();
    void Render();
};

#endif

La implementación factorizada con el puntero de ventana y algunas mejores quedará de esta forma:

#include "cube.h"
#include "window.h" // Importamos la fuente de la ventana

Cube::Cube(Window *window, int pointsPerSide)
{
    this->window = window;

    // Si el numero de puntos por lado es par le sumamos 1
    // El centro del cuadrado es el punto intermedio 0,0,0
    // Por eso necesitamos asegurarnos de poder dividirlo
    if (pointsPerSide % 2 == 0)
        pointsPerSide++;

    points = std::make_unique<Vector3[]>(pointsPerSide * pointsPerSide * pointsPerSide);
    projectedPoints = std::make_unique<Vector2[]>(pointsPerSide * pointsPerSide * pointsPerSide);

    // Array de vectores de -1 a 1 (requiere longitud impar)
    float portion = 1.0f / (pointsPerSide / 2);

    for (float x = -1.0; x <= 1; x += portion)
    {
        for (float y = -1.0; y <= 1; y += portion)
        {
            for (float z = -1.0; z <= 1; z += portion)
            {
                // std::cout << x << "," << y << "," << z << std::endl;
                points[pointsCounter++] = Vector3{x, y, z};
            }
        }
    }
}

void Cube::Update()
{
    // Set new framr rotation amounts
    rotation.x += rotationAmount.x;
    rotation.y += rotationAmount.y;
    rotation.z += rotationAmount.x;

    for (size_t i = 0; i < pointsCounter; i++)
    {
        Vector3 point = points[i];
        // Rotation transformation
        point.Rotate(rotation);
        //  Restamos la distancia de la cámara
        point.z -= window->cameraPosition.z;
        // Proyeccion del punto
        projectedPoints[i] = point.PerspectiveProjection(window->fovFactor);
    }
}

void Cube::SetRotationAmount(float x, float y, float z)
{
    rotationAmount = {x, y, z};
}

void Cube::Render()
{
    /* Dibujar proyección reposicionada al centro */
    for (size_t i = 0; i < pointsCounter; i++)
    {
        window->DrawPixel(
            projectedPoints[i].x + window->windowWidth / 2,
            projectedPoints[i].y + window->windowHeight / 2,
            0xFF00FFFF);
    }
}

Podemos pasar la referencia de la ventana al cubo, que lo crearemos en una variable privada cube:

class Window
{
private:
    /* Custom objects */
    Cube cube;

Lo inicializaremos en el método window.Setup(), así como su rotación:

#include "cube.h"

void Window::Setup()
{
    // Custom objects
    cube = Cube(this, 7);
    cube.SetRotationAmount(0.01, 0.01, 0.01);
}

Realizamos los cálculos de transformación y proyección mediante en el window.Update():

void Window::Update()
{
    // Custom objects updating
    cube.Update();
}

Y lo renderizaremos en el window.Render():

// Custom objects rendering
cube.Render();

En este punto podemos eliminar window.PostRender() del bucle while y establecer la llamada al final del propio Render ya que a partir de ahora los elementos los manejaremos desde la ventana:

void Window::Render()
{
    // Clear color buffer
    ClearColorBuffer(static_cast<uint32_t>(0xFF0000000));

    // Render the background grid
    DrawGrid(0xFF616161);

    // Custom objects renderring
    cube.Render();

    // Late rendering actions
    PostRender();
}

El resultado final será el mismo de antes:

Pero al refactorizar el código la función main quedará super limpia:

#include <iostream>
#include "window.h"

int main(int argc, char *argv[])
{
    Window window(640, 480);

    window.Init();
    window.Setup();

    while (window.running)
    {
        window.ProcessInput();
        window.Update();
        window.Render();
    }

    return 0;
}

Además en el futuro, una vez implementemos la transformación de traslación, podremos dibujar múltiples cubos con sus propiedades independientes, tiempo al tiempo.

Última edición: 05 de Junio de 2022