Triángulos, vértices y mallas¶
El renderizado de objetos tridimensionales se basa, generalmente, en mallas (meshes).
Una malla es una colección de triángulos organizados en el espacio 3D para crear la impresión de un objeto sólido:
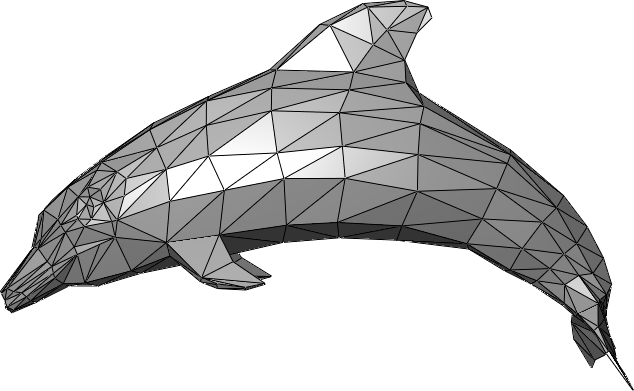
Cada uno de los triángulos, llamados caras o faces se define por tres coordenadas de esquinas llamadas comúnmente vértices, representables mediante vectores:
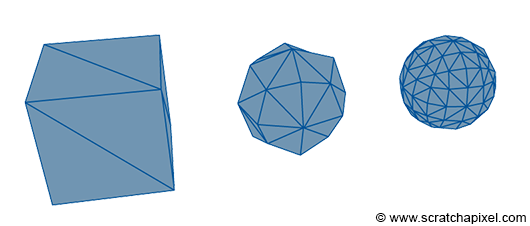
Para nuestra aplicación, un cubo está formado por una malla con 12 caras, pero como algunas comparten vértices, solo necesitamos 8 vértices para representar todas las caras:
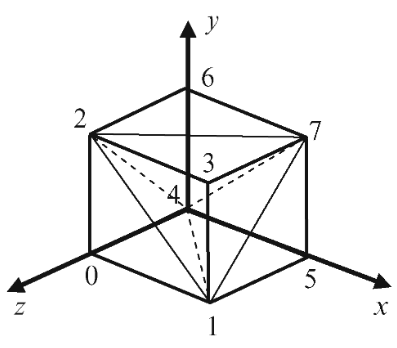
Como nuestra idea es una representación de -1 a 1 uniforme, el arreglo de vértices para un cubo podría ser este:
Vector3 vertices[8] = {
{-1, -1, -1}, // 0
{ 1, -1, -1}, // 1
{-1, 1, -1}, // 2
{ 1, 1, -1}, // 3
{-1, -1, 1}, // 4
{ 1, -1, 1}, // 5
{-1, 1, 1}, // 6
{ 1, 1, 1} // 7
}
Ahora podemos crear un nuevo arreglo definiendo las caras del cubo haciendo referencia a los índices del arreglo de vértices:
Vector3 faces[12] = {
// front ->
{1, 0, 2},
{1, 2, 3},
// back <-
{4, 5, 7},
{4, 7, 6},
// right ->
{1, 7, 5},
{1, 3, 7},
// left <-
{4, 2, 0},
{4, 6, 2},
// top ->
{2, 7, 3},
{2, 6, 7}
// bottom <-
{1, 5, 4},
{1, 4, 0}
}
El orden de los vértices en las caras es muy importante porque determina la profundidad, la dirección hacia donde mira la cara.
Una cara establecida en sentido horario, como (0, 3, 1) apunta hacia adelante, acercándose a nosotros. Pero si se establece en sentido antihorario (0, 1, 3) apunta hacia atrás, alejándose de nosotros.
Las caras deben mirar acordemente hacia donde están siendo dibujadas. La cara delantera hacia adelante (sentido horario), la caras trasera hacia atrás (sentido antihorario).
Esto se puede apreciar en la siguiente figura, donde de hecho las caras que no nos ven nunca se llegan a dibujar:
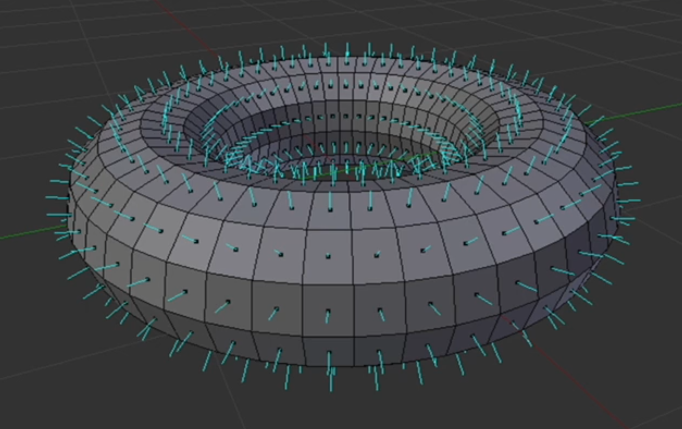
En el caso de nuestro cubo, la cara delantera, superior y derecha miran en sentido horario, mientras que la trasera, inferior e izquierda miran en sentido antiohorario.
Programando los triángulos¶
Así que vamos a ponernos manos a la obra, empezando por crear una nueva clase llama Triangle en triangle.h que almacenará los tres vertices del triángulo tanto en 3D como en 2D una vez estén ya proyectados, algo que haremos llamando la función ProjectVertex pasándole el vertexIndex y el fovFactor. También he abstraido implementaciones para las transformaciones de rotar un vértice RotateVertex y moverlo TranslateVertex:
#ifndef TRIANGLE_H
#define TRIANGLE_H
#include "vector.h"
class Triangle
{
public:
Vector3 vertices[3];
Vector2 projectedVertices[3];
void ProjectVertex(int vertexIndex, float fovFactor)
{
projectedVertices[vertexIndex] = vertices[vertexIndex].PerspectiveProjection(fovFactor);
};
void RotateVertex(int vertexIndex, Vector3 rotation)
{
vertices[vertexIndex].Rotate(rotation);
}
void TranslateVertex(int vertexIndex, Vector3 distance)
{
vertices[vertexIndex].x -= distance.x;
vertices[vertexIndex].y -= distance.y;
vertices[vertexIndex].z -= distance.z;
}
};
#endif
Dentro de la cabecera cube.h vamos a definir tres arreglos privados para gestionar los vértices, las caras y los triángulos proyectados, justo como expliqué anteriormente.
Aprovecharé para refactorizar y borrar código que ya no nos interesa:
#ifndef CUBE_H
#define CUBE_H
#include <iostream>
#include <memory>
#include "vector.h"
#include "triangle.h"
// Para prevenir dependencias cíclicas
class Window;
class Cube
{
private:
Window *window;
Vector3 rotation;
Vector3 rotationAmount;
Vector3 meshVertices[8] = {
{-1, -1, -1}, // 0
{1, -1, -1}, // 1
{-1, 1, -1}, // 2
{1, 1, -1}, // 3
{-1, -1, 1}, // 4
{1, -1, 1}, // 5
{-1, 1, 1}, // 6
{1, 1, 1} // 7
};
Vector3 meshFaces[12] = {
// front ->
{1, 0, 2},
{1, 2, 3},
// back <-
{4, 5, 7},
{4, 7, 6},
// right ->
{1, 7, 5},
{1, 3, 7},
// left <-
{4, 2, 0},
{4, 6, 2},
// top ->
{2, 7, 3},
{2, 6, 7},
// bottom <-
{1, 5, 4},
{1, 4, 0} //
};
Triangle trianglesToRender[12];
public:
Cube() = default;
Cube(Window *window) : window(window){};
void SetRotationAmount(float x, float y, float z);
void Update();
void Render();
};
#endif
Durante el evento cube.Update() vamos a iterar las caras de todos los triángulos, generando un nuevo Triangle a partir de meshVertices usando los índices de meshFaces.
A los vértices de ese triángulo Triangle.vertices les aplicaremos las transformaciones, rotación, traslación de la cámara y luego proyección a 2D, que almacenaremos en Triangle.projectedVertices y rectificación de la posición en la pantalla:
void Cube::Update()
{
// Set new framr rotation amounts
rotation.x += rotationAmount.x;
rotation.y += rotationAmount.y;
rotation.z += rotationAmount.x;
// Loop all triangle faces of the mesh
for (size_t i = 0; i < 12; i++)
{
// Create a new triangle to store data and render it later
Triangle triangle;
triangle.vertices[0] = meshVertices[static_cast<int>(meshFaces[i].x)];
triangle.vertices[1] = meshVertices[static_cast<int>(meshFaces[i].y)];
triangle.vertices[2] = meshVertices[static_cast<int>(meshFaces[i].z)];
// Loop all vertice for the face and apply transformations
for (size_t j = 0; j < 3; j++)
{
// rotate and translate vertex array form the camera
triangle.RotateVertex(j, rotation);
triangle.TranslateVertex(j, window->cameraPosition);
// project the vertex and scale it from 3D to 2D
triangle.ProjectVertex(j, window->fovFactor);
// translate the projected point to the middle screen
triangle.projectedVertices[j].x += (window->windowWidth / 2);
triangle.projectedVertices[j].y += (window->windowHeight / 2);
}
// Save the projected triangle in triangles render array
trianglesToRender[i] = triangle;
}
}
El renderizado es lo más simple del mundo, recorremos los triángulos proyectados y dibujamos cada uno de sus 3 vértices:
void Cube::Render()
{
// Loop projected triangles array and render them
for (size_t i = 0; i < 12; i++)
{
for (size_t j = 0; j < 3; j++)
{
window->DrawPixel(
trianglesToRender[i].projectedVertices[j].x,
trianglesToRender[i].projectedVertices[j].y,
0xFF00FFFF);
}
}
}
El resultado es parecido a lo que teníamos hasta ahora, pero en lugar de tener muchos puntos solo tenemos los vectores de los vértices:
La parte divertida viene a partir de ahora, pues debemos conectar los puntos e incluso pintar las superficies o añadirles texturas.
Última edición: 05 de Junio de 2022
