Rasterización de líneas¶

Una línea, o mejor dicho un segmente de una línea, es una colección infinita de puntos contínuos que conectas un punto A y un punto B.

Desde una perspectiva matemática, una línea se puede representar mediante una función, eso es una función lineal.

Dado un punto A(x0,y0) y un punto B(x1,y1) la ecuación de una línea es y = mx + c, donde m es el coheficiente para la pendiente del segmento y c es el valor interceptor de y que modifica la altura del segmento.

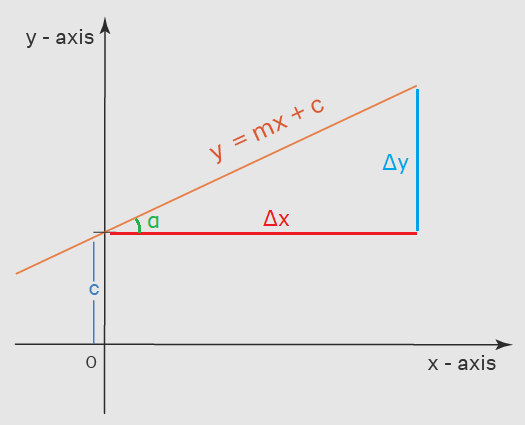
La pendiente m de una línea, es la relación entre la diferencia de la altura y1-y0 y la diferencia de anchura x1-x0:

Si la dierencia de altura Δy es pequeña para el ancho recorrido Δx, la pendiente crecerá lentamente, si la diferencia es muy grande, la pendiente crecerá rápidamente.

La pendiente m es exactamente lo mismo que la tangente del ángulo agudo (<90º) si suponemos que Δy es su lado opuesto y Δy el lado adyacente:

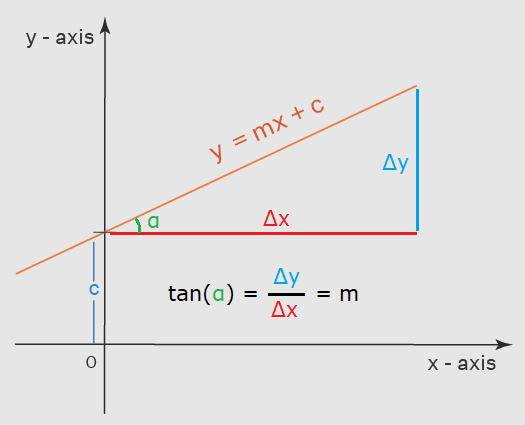
La siguiente animación ilustra la línea de la tangente dependiendo de la pendiente, tendiendo ésta a 0 cuando no hay pendiente y a infinito cuando es completamente vertical:

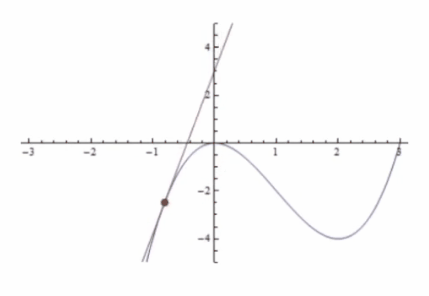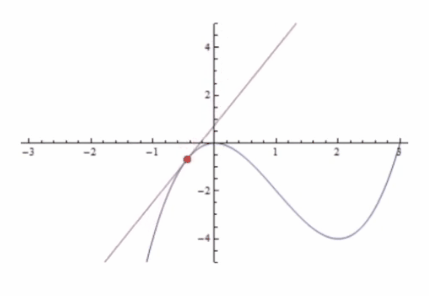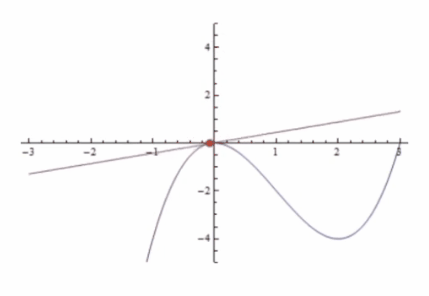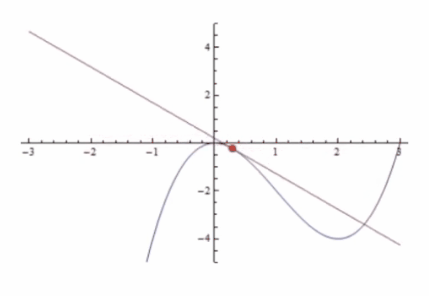
A través del signo de la pendiente podemos hacer deducciones sobre x e y:

• Si m > 1 la pendiente es muy pronunciada >45º (y > x).
• Si m < 1 la pendiente es poco pronunciada <45º (y < x).
• Si m = 1 la pendiente es equivalente a 45º (y = x).

Algoritmo DDA¶

La definición de una línea es por tanto algo perfecto, pero en realidad, como por ejemplo a la dibujarlas tenemos limitaciones.

Para dibujar líneas en la pantalla debemos hacer una aproximación mediante los píxeles y para ello existen distintos algoritmos de rasterización porque en lugar de contar con un número infinitos de puntos que forman el segmente de una línea tenemos una cantidad finita de píxeles, una trama discreta.

Los algoritmos más conocidos para raterizar líneas son:

• Digital differential analyzer (DDA)
• Bresenham line algorith
• Xiaolin Wu line algorithm

El algoritmo DDA es más sencillo de entender que el Bresenham, pero tambien más lento. Así que como estamos aprendidendo vamos a elegir el primero.

Para trazar una línea sobre la trama con DDA, debemos calcular la aproximación de cada punto de rasterizado mediante el cálculo de la pendiente en cada punto (Δy/Δx) y redondear el resultado arriba o abajo:

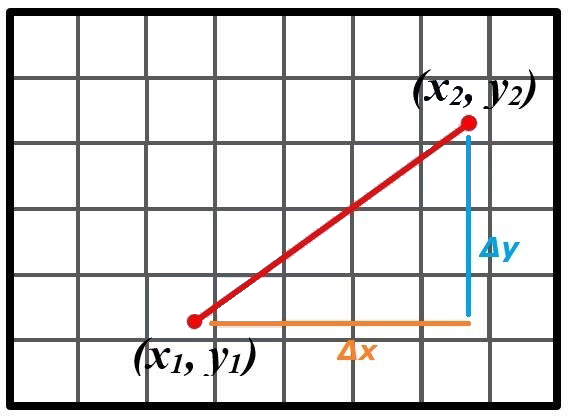
Por ejemplo, para rasterizar la línea que va de (0,0) a (4, 3) calcularemos la pendiente, que es 3:4 = 0.75. Como es menor de 1 sabemos que es poco pronunciada así que empezaremos iterando x uno a uno (puesto que hay más puntos de ancho que de alto) y calcularemos la y con la fórmula de la línea redoneando al alza o a la baja:

• y1 = 0.75 * (0) = 0 ~ 0 -> (0, 0)
• y2 = 0.75 * (1) = 0.75 ~ 1 -> (1, 1)
• y3 = 0.75 * (2) = 1.50 ~ 2 -> (2, 2)
• y4 = 0.75 * (3) = 2.25 ~ 2 -> (3, 2)
• y5 = 0.75 * (4) = 3 ~ 3 -> (4, 3)

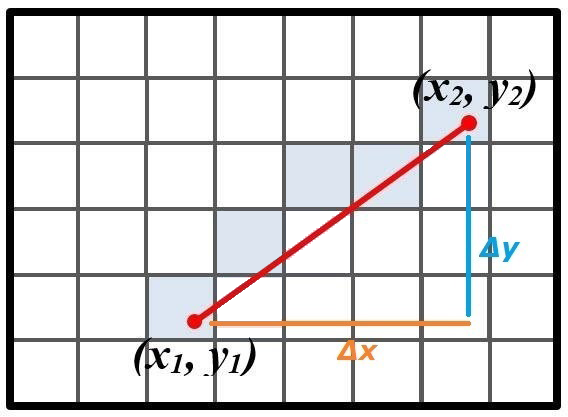
En caso de que la pendiente sea mayor que 1 sabemos que es muy pronunciada, por tanto habrá más puntos de alto que ancho y esta diferencia es importante a la hora de implementar el algoritmo:

void Window::DrawLine(int x0, int y0, int x1, int y1, uint32_t color)
{
    // Calculamos la pendiente m = Δy/Δx
    float dX = x1 - x0;
    float dY = y1 - y0;

    // Definimos la longitud con el mayor lado
    // Si pendiente < 1 tomamos dX (más ancho que alto)
    // Si pendiente >= 1 tomamos dY (más alto que ancho)
    // Nota: Como (float / 0.0) es inf no dará error,
    // incluso siendo la línea completamente vertical
    int longestSideLength = abs(dY / dX) < 1 ? abs(dX) : abs(dY);

    // Buscamos cuanto debemos ir incrementando x e y
    // Uno de ellos siempre será 1 y el otro menor que 1
    float xInc = dX / longestSideLength;
    float yInc = dY / longestSideLength;

    // Dibujamos todos los puntos para el lado más largo
    for (size_t i = 0; i < longestSideLength; i++)
    {
        // Desde el inicio (x0, y0) dibujamos todos los píxeles
        // y vamos redondeando al alza o baja hasta el final
        DrawPixel(
            round(x0 + (xInc * i)),
            round(y0 + (yInc * i)),
            0xFF00FFFF);
    }
}

Podemos probar inicialmente el algoritmo dibujando algunas líneas en lugar de renderizar los puntos proyectados del cubo:

void Cube::Render()
{
    // Render a line between all vertices
    window->DrawLine(
        0, 0, window->windowWidth / 2, window->windowHeight, 0xFF00FF00);
    window->DrawLine(
        window->windowWidth / 2, window->windowHeight, window->windowWidth / 2, 0, 0xFF0000FF);
    window->DrawLine(
        window->windowWidth / 2, 0, window->windowWidth, window->windowHeight, 0xFF00FFFF);
}

Dado que funciona sin aparentes problemas, vamo a crear un método para dibujar triángulos a partir de sus tres vértices.

void Window::DrawTriangle(int x0, int y0, int x1, int y1, int x2, int y2, uint32_t color)
{
    DrawLine(x0, y0, x1, y1, color);
    DrawLine(x1, y1, x2, y2, color);
    DrawLine(x2, y2, x0, y0, color);
}

Y ahora en nuestro cubo dibujamos los triángulos en el cube.Render():

void Cube::Render()
{
    // Loop projected triangles array and render them
    for (size_t i = 0; i < 12; i++)
    {
        window->DrawTriangle(
            trianglesToRender[i].projectedVertices[0].x,
            trianglesToRender[i].projectedVertices[0].y,
            trianglesToRender[i].projectedVertices[1].x,
            trianglesToRender[i].projectedVertices[1].y,
            trianglesToRender[i].projectedVertices[2].x,
            trianglesToRender[i].projectedVertices[2].y,
            0xFF00FFFF);
    }
}

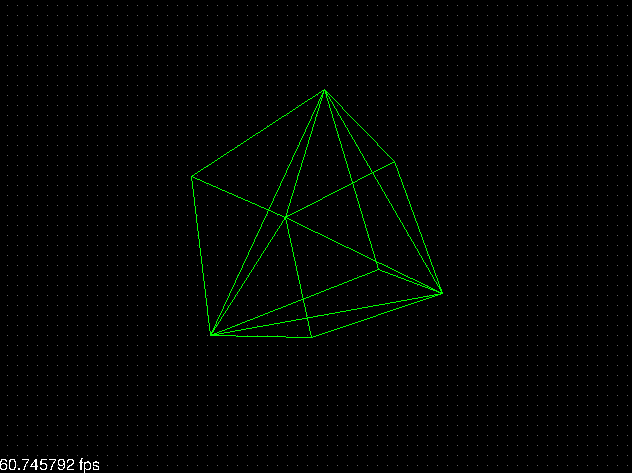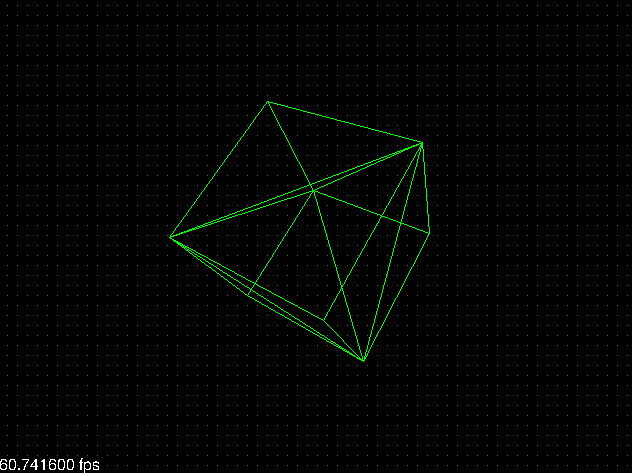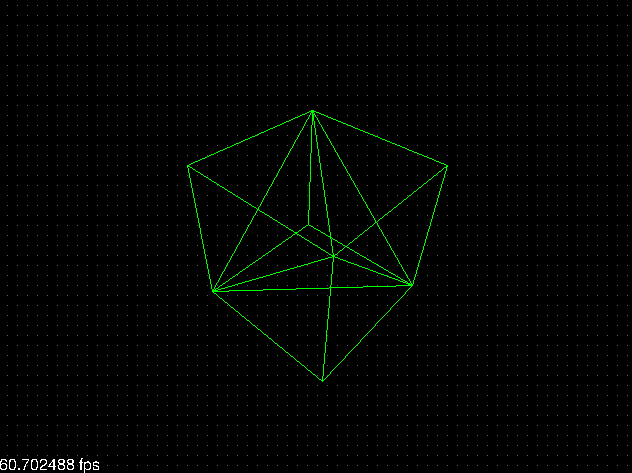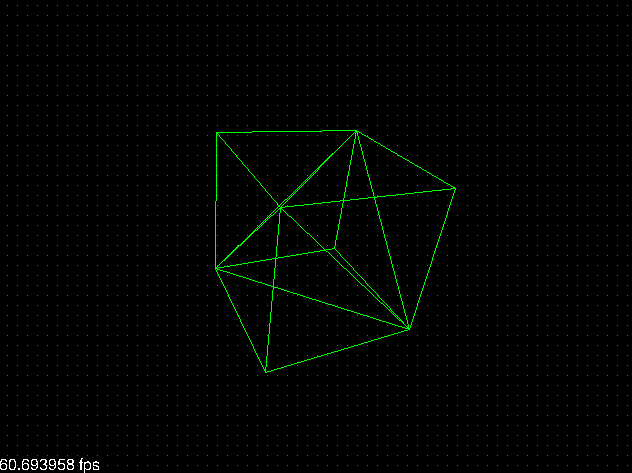
El resultado es simplemente maravilloso:

Última edición: 05 de Junio de 2022