Rasterización de triángulos¶

En esta unidad vamos a ver cómo aplicar un algoritmo para rellenar de color nuestros triángulos en lugar de simplemente trazar las líneas entre sus vértices.

Esto lo conseguiremos recorriendo cada scanline (las líneas horizontales que conforman lo que sería la pantalla), determinando si forma parte de un triángulo y activando el color en ese lugar.

Técnica Flat-Bottom Flat-Top¶

El método que vamos a utilizar para rellenar los triángulos consiste en dividir cada cara en dos triángulos, uno con el costado inferior plano y otro con el costado superior plano, de manera que coincidan en ese costado:

Primero deberemos aprender a dividir el triángulo y tan pronto lo tengamos dividido en dos triángulos, uno con inferior plano y otro con superior plano, podremos realizar un bucle de arriba hacia abajo rellenando cada línea de ambos triángulos color.

Para dividir nuestro triángulo, lo primero que tomaremos son los tres vértices del triángulo:

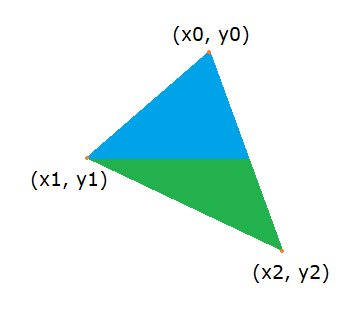
Ahora bien, ¿cómo determinamos cuál es el vértice superior? Tan pronto como empecemos a realizar transformaciones, escalar y rotar el triángulo, ese vértice dejará de ser el superior.

Pues lo que tenemos que hacer es ir reordenando los vértices en función de su altura, el componente y:

y0 < y1 < y2

Una vez ordenados los vértices debemos pensar cómo identificar los dos triángulos que comparten el lado plano y para ello deberemos identificar el segundo punto que cortará el triángulo desde (x1,y1) al que llamaremos (Mx, My):

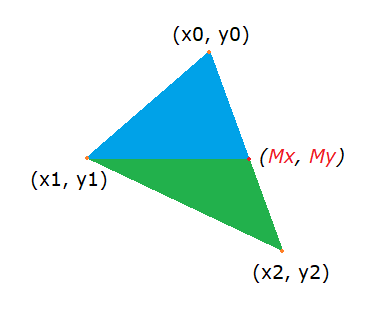
Cuando tengamos el punto medio M, podremos utilizar dos funciones para dibujar ambos triángulos rellenos:

// Dibujar triángulo con lado inferior plano
void DrawFlatBottom(x0, y0, x1, y1, Mx, My);

// Dibujar triángulo con lado superior plano
void DrawFlatTop(x1, y1, Mx, My, x2, y2);

Determinar My es simple, está a la misma altura que y1, sin embargo Mx no es tan fácil a simple vista.

Para determinar Mx acudiremos a la propiedad de los triángulos similares donde se comparte la misma proporción en sus costados para las bases y las alturas:

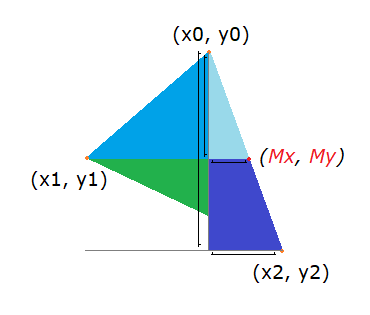
La relación quedará:

$\frac{Mx - x_0}{x_2 - x_0} = \frac{y_1 - y_0}{y_2 - y_0}$

Aplicando un poco de álgebra podemos aislar Mx:

$\\ (Mx - x_0)(y_2 - y_0) = (x_2 - x_0)(y_1 - y_0)\\\\ Mx - x_0 = \frac{(x_2 - x_0)(y_1 - y_0)}{(y_2 - y_0)}\\\\ Mx = \frac{(x_2 - x_0)(y_1 - y_0)}{(y_2 - y_0)} + x_0$

Una vez encontrada Mx ya podemos implementar la primera parte de la solución.

Supongamos el siguiente triángulo:

DrawTriangle(200, 50, 150, 300, 500, 450, 0xFF00FFFF);

Que se vería de esta forma:

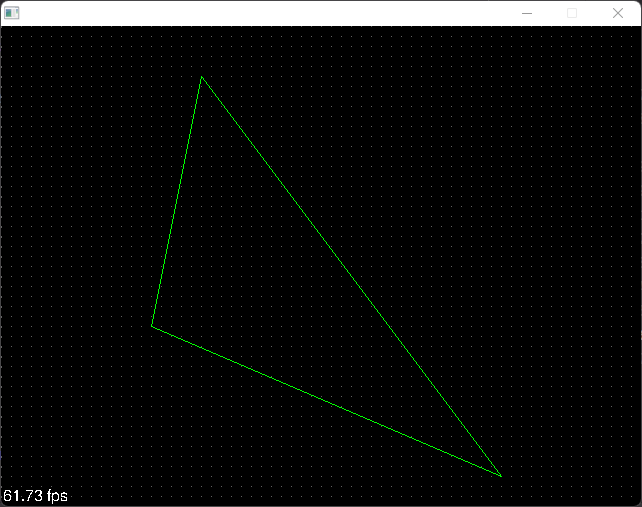
Ahora queremos dibujar el triángulo con relleno, para lo cuál empezaremos por dividir el triángulo en dos partes en un nuevo método:

DrawFilledTriangle(200, 50, 150, 300, 500, 450, 0xFF00FFFF);

Lo primero que necesitaremos es reordenar los vértices ascendientemente, quedando primero el de más arriba (y más pequeña) y así sucesivmente.

Si esto cuesta de comprender imaginemos que las y de los tres vértices son las siguientes {3, 2, 1}. El objetivo es ordenadorlos ascendentemente de manera que quede {1, 2, 3}. Para ello deberemos realizar tres intercambios:

El primer intercambio dejará como resultado {2, 3, 1}
El segundo intercambio dejará como resultado {2, 1, 3}
El tercer intercambio dejará como resultado {1, 2, 3}

Después de tres intercambios tendremos las y ordenadas.

La implementación requería crea un método SwapIntegers en la clase, luego podríamos refactorizarlo:

void Window::SwapIntegers(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void Window::DrawFilledTriangle(int x0, int y0, int x1, int y1, int x2, int y2, uint32_t color)
{
    // Reordenamiento de los vértices y0 < y1 < y2
    if (y0 > y1) // Primer intercambio
    {
        SwapIntegers(&y0, &y1);
        SwapIntegers(&x0, &x1);
    }
    if (y1 > y2) // Segundo intercambio
    {
        SwapIntegers(&y1, &y2);
        SwapIntegers(&x1, &x2);
    }
    if (y0 > y1) // Tercer intercambio
    {
        SwapIntegers(&y0, &y1);
        SwapIntegers(&x0, &x1);
    }

    // TODO: Dibujar triángulo con lado inferior plano

    // TODO: Dibujar triángulo con lado superior plano
}

Una vez ordenados los vértices debemos calcular el punto medio M para poder dibujar los dos triángulos, los cuales voy a abstraer en dos nuevos métodos FillFlatBottomTriangle y FillFlatTopTriangle:

void Window::DrawFilledTriangle(int x0, int y0, int x1, int y1, int x2, int y2, uint32_t color)
{
    // Reordenamiento de los vértices y0 < y1 < y2
    if (y0 > y1) // Primer intercambio
    {
        SwapIntegers(&y0, &y1);
        SwapIntegers(&x0, &x1);
    }
    if (y1 > y2) // Segundo intercambio
    {
        SwapIntegers(&y1, &y2);
        SwapIntegers(&x1, &x2);
    }
    if (y0 > y1) // Tercer intercambio
    {
        SwapIntegers(&y0, &y1);
        SwapIntegers(&x0, &x1);
    }    

    // Calcular el vértice (Mx, My) usando similitudes
    int Mx = (((x2 - x0) * (y1 - y0)) / static_cast<float>((y2 - y0))) + x0;
    int My = y1;

    // Dibujar triángulo con lado inferior plano
    FillFlatBottomTriangle(x0, y0, x1, y1, Mx, My, color);
    // Dibujar triángulo con lado superior plano
    FillFlatTopTriangle(x1, y1, Mx, My, x2, y2, color);
}

Ahora nos toca implementar los algoritmos para dibujar ambos triángulos.

El algoritmo para dibujar el triángulo con lado inferior plano enumera los sigientes pasos:

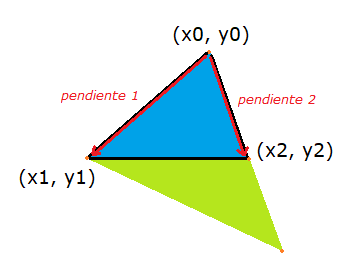
Empezaremos desde arriba en el vértice (x0, y0).
Calcularemos la pendiente 1 y la pendiente 2.
Realizaremos un bucle para todos los scanlines desde y0 a y2:
1. En base a las pendientes, calcularemos cada píxel de inicio x_start y final x_end.
2. Dibujaremos la línea que va desde x_start hasta x_end.
3. En base a los valores de la pendiente, incrementar x_start y x_end para el siguiente scanline.

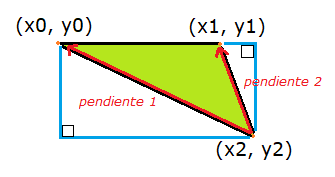
Para calcular las pendientes solo debemos encontrar la relación entre el alto y ancho de los triángulos que se forman:

$m = \frac{\Delta y}{\Delta x}$

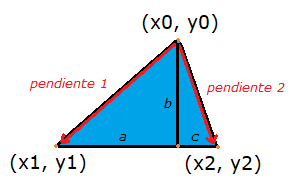
m1 = b/a = (y2 - y0) / (x2 - x0) 
m2 = b/c = (y1 - y0) / (x0 - x1)

Con la pendiente podemos aplicar lo que hicimos con el algoritmo DDA y determinarl os puntos de inicio y fin de x para cada y.

El código quedará:

void Window::FillFlatBottomTriangle(int x0, int y0, int x1, int y1, int x2, int y2, uint32_t color)
{
    // Algoritmo propio
    float m1 = -((y1 - y0) / static_cast<float>((x0 - x1))); // m1 izquierda -
    float m2 = (y2 - y0) / static_cast<float>((x2 - x0));    // m2 derecha +

    for (int i = 0; i < (y1 - y0); i++)
    {
        DrawLine(x0 + (i / m1), y0 + i, x0 + (i / m2), y0 + i, color);
    }
}

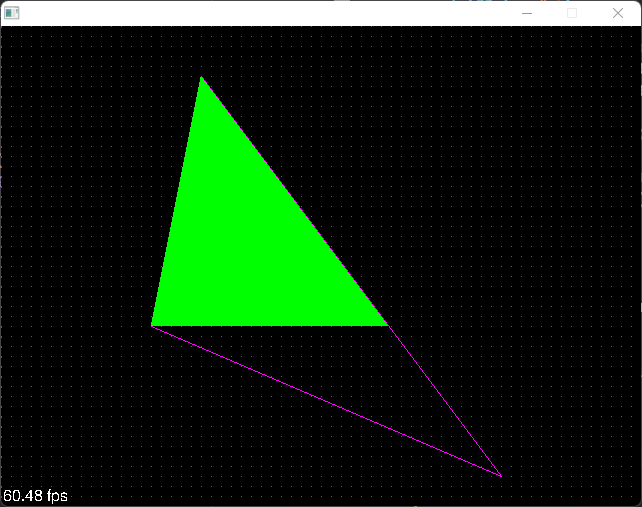
El resultado en este punto será el triángulo superior:

DrawTriangle(200, 50, 150, 300, 500, 450, 0xFFFF00FF);
DrawFilledTriangle(200, 50, 150, 300, 500, 450, 0xFF00FF00);

El algoritmo para dibujar el triángulo con lado superior plano enumera los sigientes pasos:

Empezaremos desde abajo en el vértice (x2, y2).
Calcularemos la pendiente 1 y la pendiente 2.
Realizaremos un bucle para todos los scanlines desde y2 a y0:
1. En base a las pendientes, calcularemos cada píxel de inicio x_start y final x_end.
2. Dibujaremos la línea que va desde x_start hasta x_end.
3. En base a los valores de la pendiente, decrementar x_start y x_end para el siguiente scanline.

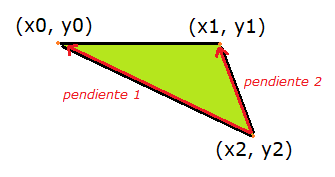
Quizá en este triángulo no queda muy claro cómo calcular las pendientes, la siguiente figura muestra esas pendientes en base a la altura y anchura marcadas en azul:

Y el código quedará:

void Window::FillFlatTopTriangle(int x0, int y0, int x1, int y1, int x2, int y2, uint32_t color)
{
    // Algoritmo propio
    float m1 = -((y2 - y0) / static_cast<float>((x2 - x0))); // m1 izquierda -
    float m2 = -((y2 - y1) / static_cast<float>((x2 - x1))); // m2 izquierda -

    for (int i = 0; i <= (y2 - y1); i++)
    {
        DrawLine(x2 + (i / m1), y2 - i, x2 + (i / m2), y2 - i, color);
    }
}

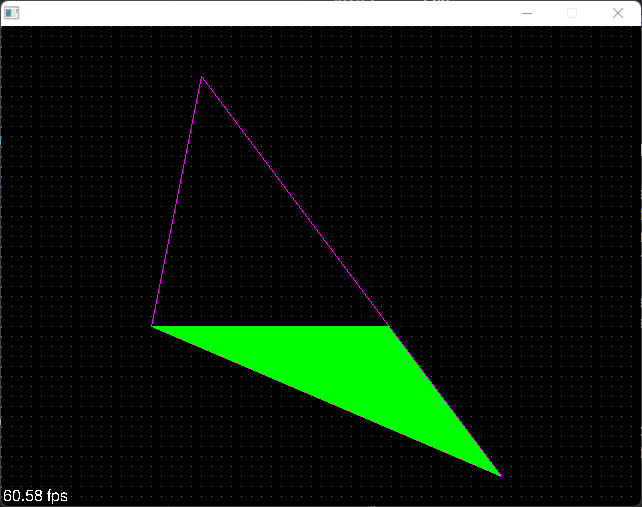
El resultado en este punto será el triángulo inferior:

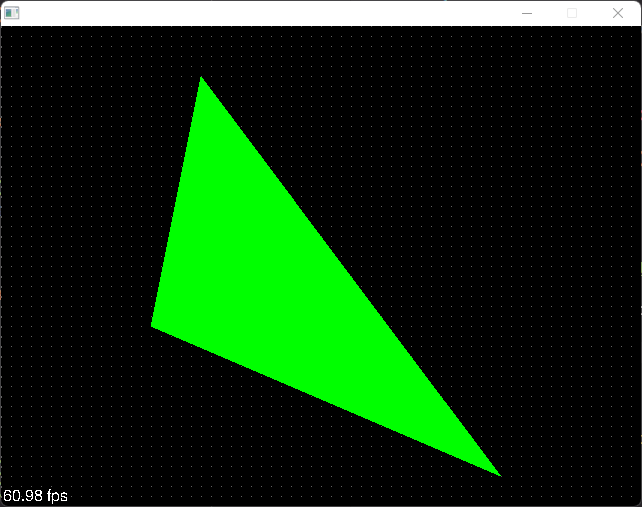
Con ambos triángulos activos tendremos la cara completa rasterizada:

Así que vamos a probar como queda nuestro nuevo método para pintar las caras del cubo, dibujando los triángulos rasterizados en blanco y por encima los vértices en negro:

void Mesh::Render()
{
    // Loop projected triangles array and render them
    for (size_t i = 0; i < triangles.size(); i++)
    {
        // If culling is true bypass the current triangle
        if (triangles[i].culling)
            continue;

        window->DrawFilledTriangle(
            triangles[i].projectedVertices[0].x, 
            triangles[i].projectedVertices[0].y,
            triangles[i].projectedVertices[1].x, 
            triangles[i].projectedVertices[1].y,
            triangles[i].projectedVertices[2].x, 
            triangles[i].projectedVertices[2].y,
            0xFFFFFFFF);

        window->DrawTriangle(
            triangles[i].projectedVertices[0].x, 
            triangles[i].projectedVertices[0].y,
            triangles[i].projectedVertices[1].x, 
            triangles[i].projectedVertices[1].y,
            triangles[i].projectedVertices[2].x, 
            triangles[i].projectedVertices[2].y,
            0xFF000000);
    }
}

Si lo probamos...

Lo tenemos perfecto pero hay una optimización que debemos añadir lo antes posible para prevenir divisiones entre cero, que en C++ al dividr números flotantes dan lugar a valores potencialmente infinitos.

Evitar división entre cero¶

Cuando una cara tiene un lado plano debemos podemos saltataros el dibujado de uno de los dos triángulos, ya que simplemente será una línea recta.

El primer caso es que la altura del segundo vértice y1 y tercero y2 sean la misma, por ejemplo en una cara como esta:

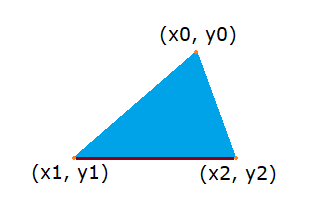
En ese caso haremos un by-pass para dibujar únicamente el triángulo superior:

if (y1 == y2)
{
    FillFlatBottomTriangle(x0, y0, x1, y1, x2, y2, color);
}

En el segundo caso en que la altura del primer vértice y0 y la del segundo y1 sea la misma:

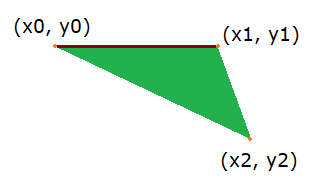
En este caso haremos un by-pass para dibujar únicamente el triángulo inferior:

else if (y1 == y2)
{
    FillFlatTopTriangle(x0, y0, x1, y1, x2, y2, color);
}

En cualquier otro caso dibujaremos la cara a partir de los dos triángulos:

else
{
    // Calcular el vértice (Mx, My) usando similitudes
    int Mx = (((x2 - x0) * (y1 - y0)) / static_cast<float>((y2 - y0))) + x0;
    int My = y1;

    // Dibujar triángulo con lado inferior plano
    FillFlatBottomTriangle(x0, y0, x1, y1, Mx, My, color);
    // Dibujar triángulo con lado superior plano
    FillFlatTopTriangle(x1, y1, Mx, My, x2, y2, color);
}

El resultado será el mismo pero habremos optimizado bastante el código al saltarnos el renderizado y los cálculos del punto medio M cuando no nos hace falta:

Última edición: 05 de Junio de 2022