Operaciones con matrices¶

Una matriz es un arreglo rectangular de valores dispuestos en filas y columnas:

Esencialmente es una construcción matemática para representar valores ordenados.

La dimensión de una matriz es la expresión de su longitud por su altura.

En la matriz siguiente matriz podemos observar dos filas y tres columnas:

La dimensión de la matriz es 2 x 3 (2 filas x 3 columnas).

En la siguiente matriz:

La dimensión es 3x2 (3 filas x 2 columnas).

Más allá de tener una dimensión, en cada uno de los lugares de la matriz tenemos elementos:

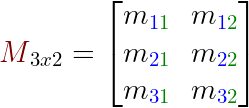
En una matriz M cuya dimensión es 3x2 podemos representar sus elementos m en función de su fila y columna.

Así que una matriz es una serie de valores dispuestos o presentados de forma rectangular, a modo de tabla.

¿Pero para qué sirven?

Una utilidad de las matrices es ayudarnos a representar datos que no se pueden medir en una dimensión. Por ejemplo, un contador es un número escalar con una sola dimensión:

Nº de manzanas
--------------
3

Pero si cada manzana tiene diferentes propiedades: variedad, color, sabor... No podemos representarlo en un número, necesitamos una estructura de dos dimensiones:

Variedad     Color       Sabor
------------------------------------
Fuji         Naranja     Muy dulce
Golden       Amarillo    Menos dulce
Pink Lady    Rosadoo     Algo ácido

Las tablas y hojas de cálculos (spreadsheets) son formas de representar estos datos multidimensionales.

Otra utilidad de las matrices es su uso para describir sistemas de ecuaciones lineales en las matemáticas, donde cada entrada representa un coeficiente de la ecuación original.

Por ejemplo este sistema lineal:

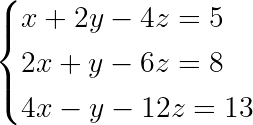
Expresado en forma de matriz aumentada:

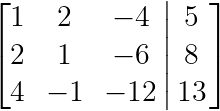
En los gráficos por computadora, una aplicación de las matrices es su habilidad para convertir conjuntos de datos geométricos a otros sistemas de coordenadas. Por ejemplo, una matriz de multiplicación nos ayudará a representar transformaciones como la traslación, rotación, proyección y muchas otras.

Adición de matrices¶

La adición o suma de matrices es un cálculo simple entre dos matrices de la misma dimensión. Los elementos de cada posición se suman dando lugar a una nueva matriz con la misma dimensión:

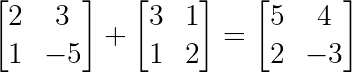
Sustracción de matrices¶

La sustracción o resta de matrices es otro cálculo simple entre dos matrices de la misma dimensión. Los elementos de cada posición se restan dando lugar a una nueva matriz con la misma dimensión:

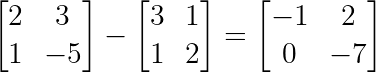
Multiplicación de matrices¶

La multiplicación de matrices no es un cálculo simple porque no se basa en multiplicar los elementos de la misma posición sino en multiplicar las filas de la primera matriz por las columnas de la segunda:

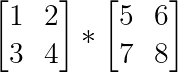
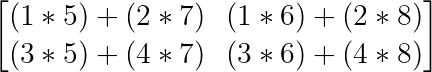
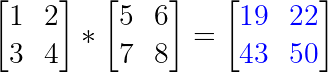
El punto interesante es que, si recordamos los vectores, podemos ver un patrón en la forma en que se multiplican las filas y las columnas. Me refiero ni más ni menos que al producto escalar.

Debemos recordar las propiedades de la mulitplicación de matrices:

1. Una multiplicación de matrices solo es posible cuando el número de columnas de la matriz izquierda M es equivalente al número de filas de la matriz derecha M.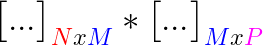

   

2. La dimensión de la matriz resultante tendrá el mismo número de filas que la matriz izquierda N y el mismo número de columnas que la matriz derecha P.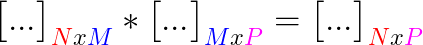

   

3. La multiplicación de matrices no es conmutativa, el orden afecta al resultado.

   

Matriz de identidad¶

Una matriz de identididad, también llamada unit matrix o eye matrix, es una matriz con todos los elementos diagonales en 1 y los demás en 0.

1. Para cualquier matriz cuadrada M de dimensión nxn siempre existe una matriz de identidad I: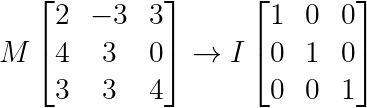

   

2. Multiplicar una matriz cuadrada M por su matriz de identidad I siempre resultará en la propia matriz M, es por así decirlo como multiplicar un número por 1: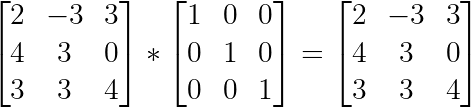

   

Ejemplo de rotación 2D con matrices¶

Por último en esta sección vamos a repasar una aplicación de las matrices para representar una transformación lineal como sería una rotación en 2D.

Anteriormente ya hablamos de la forma de rotar un vector por un ángulo:

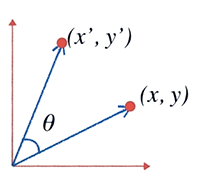
Llegamos a la conclusión que para hacerlo debíamos aplicar las fórmulas:

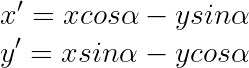
Esto se puede representar con la siguiente matriz de rotación 2D:

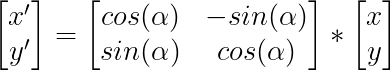
Esta multiplicación de matrices dará como resultado:

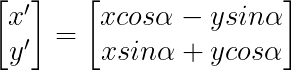
Como veamos es un atajo para conseguir lo mismo que hicimos trabajando con vectores pero dispuesto de una forma más cómoda.

Última edición: 05 de Junio de 2022