Matrices de transformación 3D¶

En este bloque vamos a repasar las diferentes matrices de transformación para aplicar en entornos 3D. Estas matrices se pueden presentar individualmente o de forma combinada (traslación, rotación, escalado o transformación de mundo).

En álgebra lineal, las transformaciones lineales pueden representarse con matrices. Generalmente se utilizan matrices 4x4 para representar transformaciones 3D:

$\begin{bmatrix}m & m & m & m \\m & m& m & m \\m & m & m & m \\m & m & m & m \\\end{bmatrix}{\color{Red}* }\begin{bmatrix}x \\y \\z \\ \\\end{bmatrix}$

Utilizamos matrices 4x4 en lugar de 3x3 porque algunas transformaciones especiales, como la traslación, requiere una columna/fila extra para realizarse correctamente.

Para permtir la multiplicación matriz-vector añadiremos un componente w al vector al que por ahora daremos el valor 1:

$\begin{bmatrix}m & m & m & m \\m & m& m & m \\m & m & m & m \\m & m & m & m \\\end{bmatrix}{\color{Red}* }\begin{bmatrix}x \\y \\z \\1 \\\end{bmatrix}$

Matriz de escalado 3D¶

La matriz que aplicaremos para realizar un escalado 3D es la siguiente:

$\begin{bmatrix}{\color{Blue} sx} & 0 & 0 & 0 \\0 & {\color{Blue} sy}& 0 & 0 \\0 & 0 & {\color{Blue} sz} & 0 \\0 & 0 & 0 & 1 \\\end{bmatrix}{\color{Red}* }\begin{bmatrix}x \\y \\z \\1 \\\end{bmatrix}$

Aquí sx, sy y sz representan el factor de escalado para cada componente.

El resultado de aplicarla será el siguiente:

$\begin{bmatrix}({\color{Blue} sx} * x)+ 0 + 0 + 0 \\0 + ({\color{Blue} sy} * y)+ 0 + 0 \\0 + 0 + ({\color{Blue} sz} * z) + 0 \\0 + 0 + 0 + (1 *1) \\\end{bmatrix}=\begin{bmatrix}{\color{Blue} sx} * x \\{\color{Blue} sy} * y \\{\color{Blue} sz} * z \\1 \\\end{bmatrix}$

Para poder aplicar esta funcionalidad necesitamos modificar el código, ya que en él no estamos utilizando matrices sino que estamos aplicando las fórmulas trigonométricas manualmente.

Así que lo primero será definir nuestro nuevo tipo Matrix4:

#ifndef MATRIX_H
#define MATRIX_H

#include "vector.h"

class Matrix4
{
public:
    float m[4][4];

    static Matrix4 IdentityMatrix()
    {
        //  |  1  0  0  0 |
        //  |  0  1  0  0 |
        //  |  0  0  1  0 |
        //  |  0  0  0  1 |

        return Matrix4{{{1, 0, 0, 0},
                        {0, 1, 0, 0},
                        {0, 0, 1, 0},
                        {0, 0, 0, 1}}};;
    }

    static Matrix4 ScalationMatrix(float x, float y, float z)
    {
        //  | sx  0  0  0 |
        //  |  0 sy  0  0 |
        //  |  0  0 sz  0 |
        //  |  0  0  0  1 |
        Matrix4 m = Matrix4::IdentityMatrix();
        m.m[0][0] = x;
        m.m[1][1] = y;
        m.m[2][2] = z;
        return m;
    }
};

#endif

Ahora debemos de hacer uso de esta nueva clase matriz y sus métodos en el mesh.

Primero añadiremos vectores para manejar la rotación, escalado y traslación, preparando ya el terreno también para las próximas transformaciones:

class Mesh
{
public:
    Vector3 scale{1, 1, 1};
    Vector3 rotation{0, 0, 0};
    Vector3 translation{0, 0, 0};
}

Llamaremos al método de escalado para cada vértice del triángulo en el método mesh.Update():

/*** Apply transformations for all face vertices ***/
for (size_t j = 0; j < 3; j++)
{
    // ORDER MATTERS, REALLY IMPORTANT
    // 1. Scale using the matrix
    triangles[i].ScaleVertex(j, scale);
    // 2. Rotate using the matrices
    // triangles[i].RotateVertex(j, rotation);
    // 3. Translation using the matrix
    // triangles[i].TranslateVertex(j, translation);
}

En este método multiplicaremos el vector de escalado por la matriz de escalado, pero necesitamos tenerlo en formato Vector4 para que sean compatibles. Una vez realizado el cálculo estableceremos el vertice con el nuevo valor transformado:

void ScaleVertex(int vertexIndex, Vector3 scale)
{
    // Use a matrix to transform scale the origin vertex
    Vector4 transformedVertex{vertices[vertexIndex]};
    transformedVertex = transformedVertex * Matrix4::ScalationMatrix(scale.x, scale.y, scale.z);
    vertices[vertexIndex] = transformedVertex.ToVector3();
}

El nuevo tipo de dato Vector4 es esencialmente un Vector3 con la capacidad de ser multiplicado por una Matrix4. Tiene un constructor base y uno a partir de un Vector3, así como métodos para transformarlo a un Vector3 y las sobrecargas de la multiplicación pasándole una Matrix4:

#ifndef VECTOR_H
#define VECTOR_H

#include <iostream>

class Matrix4; /* Pre declaration */
class Vector4
{
public:
    double x{0};
    double y{0};
    double z{0};
    double w{0};

    Vector4() = default;
    Vector4(Vector3 v) : x(v.x), y(v.y), z(v.z), w(1){};
    Vector3 ToVector3();

    Vector4 operator*(Matrix4 m) const;
};
#endif

// Definición
Vector3 Vector4::ToVector3()
{
    return Vector3(x, y, z);
}

Vector4 Vector4::operator*(Matrix4 m) const
{
    Vector4 result;
    result.x = m.m[0][0] * x + m.m[0][1] * y + m.m[0][2] * z + m.m[0][3] * w;
    result.y = m.m[1][0] * x + m.m[1][1] * y + m.m[1][2] * z + m.m[1][3] * w;
    result.z = m.m[2][0] * x + m.m[2][1] * y + m.m[2][2] * z + m.m[2][3] * w;
    result.w = m.m[3][0] * x + m.m[3][1] * y + m.m[3][2] * z + m.m[3][3] * w;
    return result;
}

Con esto tendremos el sistema preparado, podemos configurar la interfaz para intentar modificar el vector de escalado en tiempo real mediante un nuevo método de la malla para establecer el escalado:

void Mesh::SetScale(float *scale)
{
    this->scale = {scale[0], scale[1], scale[2]};
}

En la interfaz añadiremos el widget para el nuevo campo modelScale:

class Window
{
public:
    /*Model settings */
    float modelScale[3] = {1, 1, 1};
}

El código para ImGui y debajo para establecer los cambios:

ImGui::Separator();
ImGui::Text("Escalado del modelo");
ImGui::SliderFloat3("Scale", modelScale, 0, 5);

// Update Model Settings
mesh.SetScale(modelScale);

De paso modificaremos un poco la rotación ya que realmente no queremos una rotación automatizada, sino que podamos establecer la rotación actual a mano:

class Window
{
public:
    /*Model settings */
    float modelRotation[3] = {0, 0, 0};
}

El widget:

ImGui::Text("Vector de rotación");
ImGui::SliderFloat3("Rotation", modelRotation, 0, 10);

// Update Model Settings
mesh.SetRotation(modelRotation);

Éste llamará a nuestro nuevo método:

void Mesh::SetRotation(float *rotation)
{
    this->rotation = {rotation[0], rotation[1], rotation[2]};
}

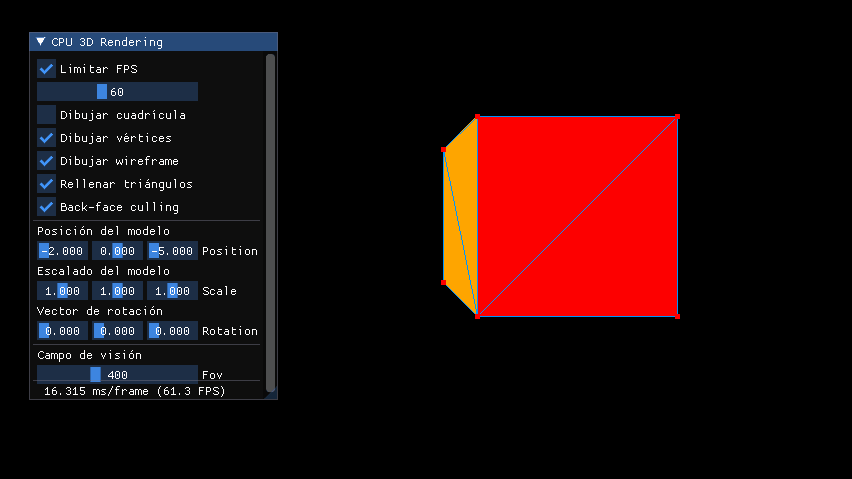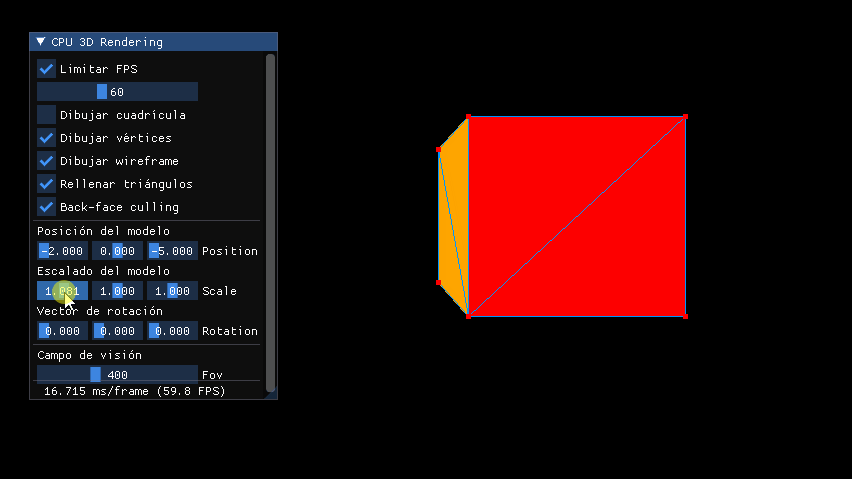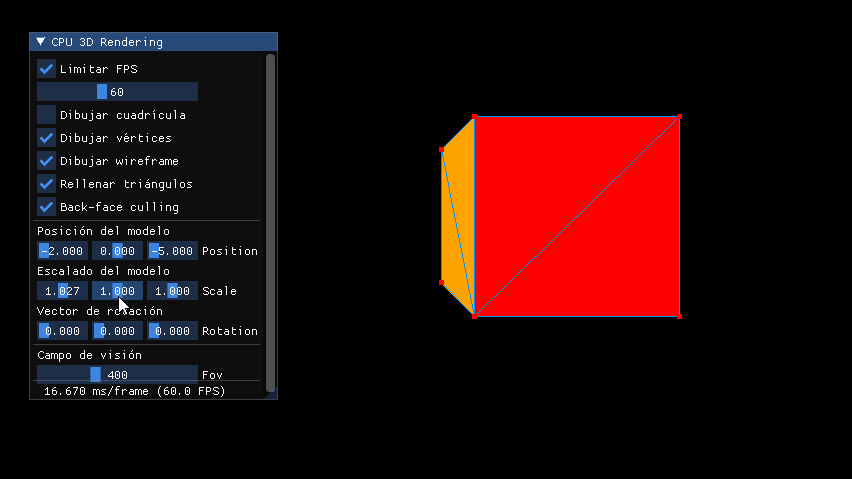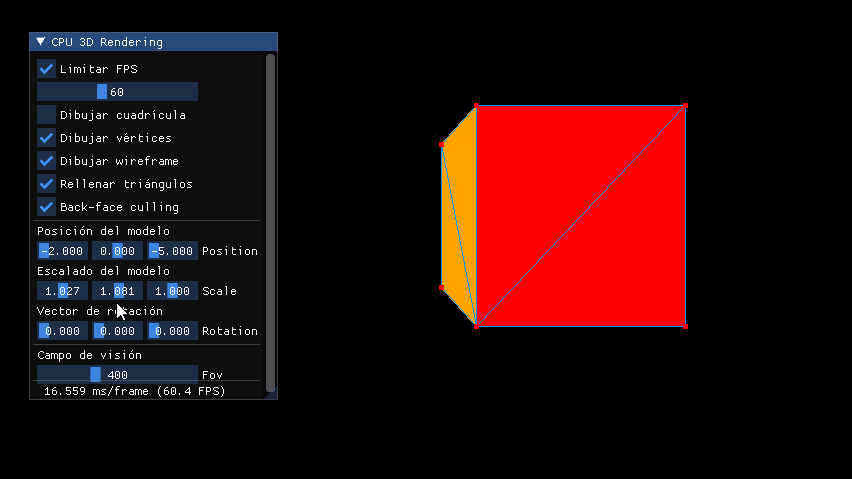
Por ahora este es el resultado del escalado con matrices:

Matriz de traslación 3D¶

La matriz que aplicaremos para realizar una traslación, modificar la posición en el espacio de la malla, es la siguiente:

$\begin{bmatrix}1&0&0&{\color{Blue}tx}\\0&1&0&{\color{Blue}ty}\\0&0&1&{\color{Blue}tz}\\0&0&0&1\\\end{bmatrix}{\color{Red}*}\begin{bmatrix}x\\y\\z\\1\\\end{bmatrix}$

En esta matriz, la última columna extra, almacena la cantidad de traslación en cada componente tx, ty y tz.

El resultado de aplicarla será el siguiente:

$\begin{bmatrix}x+0+0+{\color{Blue} tx}\\0+y+0+{\color{Blue} ty}\\0+0+z+{\color{Blue} tz}\\0+0+0+1\\\end{bmatrix}=\begin{bmatrix}{x+\color{Blue}tx}\\y+{\color{Blue}ty}\\z+{\color{Blue}tz}\\1\\\end{bmatrix}$

La cuarta columna es la única forma en que podemos representar la traslación en una matriz 4x4.

La implementación es muy simple:

static Matrix4 TranslationMatrix(float x, float y, float z)
{
    //  |  1  0  0  tx  |
    //  |  0  1  0  ty  |
    //  |  0  0  1  tz  |
    //  |  0  0  0   1  |
    Matrix4 m = Matrix4::IdentityMatrix();
    m.m[0][3] = x;
    m.m[1][3] = y;
    m.m[2][3] = z;
    return m;
}

El nuevo método para trasladar un vértice en Triangle es:

void TranslateVertex(int vertexIndex, Vector3 translation)
{
    // Use a matrix to transform translate the origin vertex
    Vector4 transformedVertex{vertices[vertexIndex]};
    transformedVertex = transformedVertex * Matrix4::TranslationMatrix(translation.x, translation.y, translation.z);
    vertices[vertexIndex] = transformedVertex.ToVector3();
}

Lo aplicaremos durante las transformaciones en mesh.Update() al final de todo, después del escalado y la rotación:

/*** Apply transformations for all face vertices ***/
for (size_t j = 0; j < 3; j++)
{
    // ORDER MATTERS, REALLY IMPORTANT
    // 1. Scale using the matrix
    triangles[i].ScaleVertex(j, scale);
    // 2. Rotate using the matrices
    // triangles[i].RotateVertex(j, rotation);
    // 3. Translation using the matrix
    triangles[i].TranslateVertex(j, translation);
}

Para modificar la traslación desde la interfaz añadirmeos al mesh el método con la rectificación de la posición de la cámara window.cameraPosition préviamente establecida en {0,0,-5}:

void Mesh::SetTranslation(float *translation)
{
    // Con rectificación de origen
    this->translation = {translation[0] - window->cameraPosition[0], translation[1] - window->cameraPosition[1], translation[2] - window->cameraPosition[2]};
}

Tanto la traslación como la posición de la cámara la podremos modificaf en la interfaz:

ImGui::Text("Traslación del modelo");
ImGui::SliderFloat3("Translation", modelTranslation, -5, 5);
ImGui::Separator();
ImGui::Text("Posición cámara (X,Y,Z)");
ImGui::SliderFloat3("Camera", cameraPosition, -5, 5);

// Update Model Settings
mesh.SetTranslation(modelTranslation);

Esta variable window.modelTranslation la adaptaremos de modelPosition, pues el nombre es ahora más acertado:

/* Model settings */
float modelScale[3] = {1, 1, 1};
float modelRotation[3] = {0, 0, 0};
float modelTranslation[3] = {0, 0, 0};

/* Camera settings */
float cameraPosition[3] = {0, 0, -5};
int fovFactor = 400;

Con esto deberíamos ser capaces de cambiar la posición del modelo y de la cámara correctamente:

Matriz de rotación 3D¶

La rotación 3D se realiza mediante el bloqueo de un eje, por lo que tendremos 3 variantes de la matriz de rotación dependiendo del eje alrededor del cuál queramos rotar. Por lo demás es aplicar la lógica que vimos para realizar una rotación de un vector en 2D.

La matriz de rotación alrededor del eje Z, manteniéndo ese eje intocable (tercera fila y tercera columna) es:

$\begin{bmatrix}{\color{Blue} cos(\alpha)}&{\color{Blue} -sin(\alpha)}&0&0\\{\color{Blue} sin(\alpha)}&{\color{Blue} cos(\alpha)}&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}{\color{Red}*}\begin{bmatrix}x\\y\\z\\1\\\end{bmatrix}$

static Matrix4 RotationZMatrix(float angle)
{
    float c = cos(angle);
    float s = sin(angle);
    //  |  c -s  0  0  |
    //  |  s  c  0  0  |
    //  |  0  0  1  0  |
    //  |  0  0  0  1  |
    Matrix4 m = Matrix4::IdentityMatrix();
    m.m[0][0] = c;
    m.m[0][1] = -s;
    m.m[1][0] = s;
    m.m[1][1] = c;
    return m;
}

La matriz de rotación alrededor del eje X, manteniéndo ese eje intocable (primera fila y primera columna) es:

$\begin{bmatrix}1&0&0&0\\0&{\color{Blue} cos(\alpha)}&{\color{Blue} -sin(\alpha)}&0\\0&{\color{Blue} sin(\alpha)}&{\color{Blue} cos(\alpha)}&0\\0&0&0&1\\\end{bmatrix}{\color{Red}*}\begin{bmatrix}x\\y\\z\\1\\\end{bmatrix}$

static Matrix4 RotationXMatrix(float angle)
{
    float c = cos(angle);
    float s = sin(angle);
    //  |  1  0  0  0  |
    //  |  0  c -s  0  |
    //  |  0  s  c  0  |
    //  |  0  0  0  1  |
    Matrix4 m = Matrix4::IdentityMatrix();
    m.m[1][1] = c;
    m.m[1][2] = -s;
    m.m[2][1] = s;
    m.m[2][2] = c;
    return m;
}

La matriz de rotación alrededor del eje Y, manteniéndo ese eje intocable (segunda fila y segunda columna) es:

$\begin{bmatrix}{\color{Blue} cos(\alpha)}&0&{\color{Orange} sin(\alpha)}&0\\0&1&0&0\\{\color{Orange} -sin(\alpha)}&0&{\color{Blue} cos(\alpha)}&0\\0&0&0&1\\\end{bmatrix}{\color{Red}*}\begin{bmatrix}x\\y\\z\\1\\\end{bmatrix}$

static Matrix4 RotationYMatrix(float angle)
{
    float c = cos(angle);
    float s = sin(angle);
    //  |  c  0  s  0  |
    //  |  0  1  0  0  |
    //  | -s  0  c  0  |
    //  |  0  0  0  1  |
    Matrix4 m = Matrix4::IdentityMatrix();
    m.m[0][0] = c;
    m.m[0][2] = s;
    m.m[2][0] = -s;
    m.m[2][2] = c;
    return m;
}

Es importante notar que el signo de los senos está cambiado en todas las matrices. La notación formal es para cuando Z crece en sentido horario, en nuestro sistema hemos aplicado lo contrario (crece en sentido antihorario), por tanto los senos estás negados.

En cualquier caso aplicaremos esta rotación en el mesh.Update, siempre después del escalado y antes de la traslación. Es muy importante porque sino realizaremos la rotación respecto a la posición trasladada:

/*** Apply transformations for all face vertices ***/
for (size_t j = 0; j < 3; j++)
{
    // ORDER MATTERS, REALLY IMPORTANT
    // 1. Scale using the matrix
    triangles[i].ScaleVertex(j, scale);
    // 2. Rotate using the matrices
    triangles[i].RotateVertex(j, rotation);
    // 3. Translation using the matrix
    triangles[i].TranslateVertex(j, translation);
}

El método de rotación de Triangle hará uso de las tres matrices de rotación:

void RotateVertex(int vertexIndex, Vector3 rotation)
{
    // Use a matrix to transform rotate the origin vertex
    Vector4 transformedVertex{vertices[vertexIndex]};
    transformedVertex = transformedVertex * Matrix4::RotationXMatrix(rotation.x);
    transformedVertex = transformedVertex * Matrix4::RotationYMatrix(rotation.y);
    transformedVertex = transformedVertex * Matrix4::RotationZMatrix(rotation.z);
    vertices[vertexIndex] = transformedVertex.ToVector3();
}

En principio podemos reutilizar lo que teníamos de la interfaz y ya tendremos un visualizador de modelos 3D bastante completo:

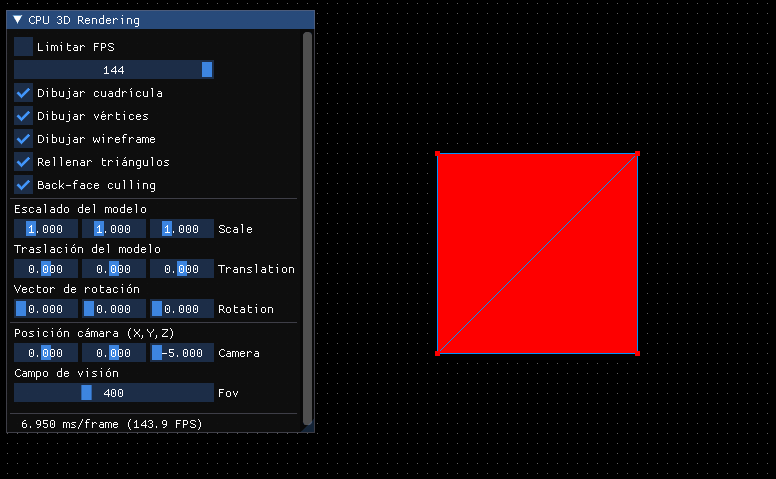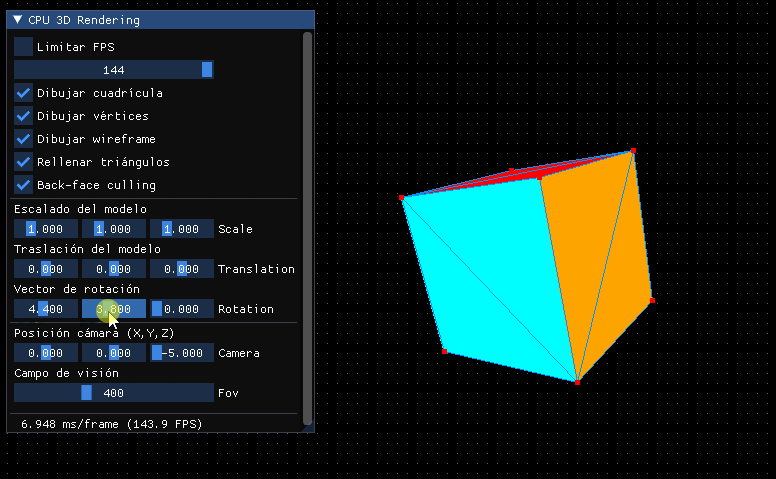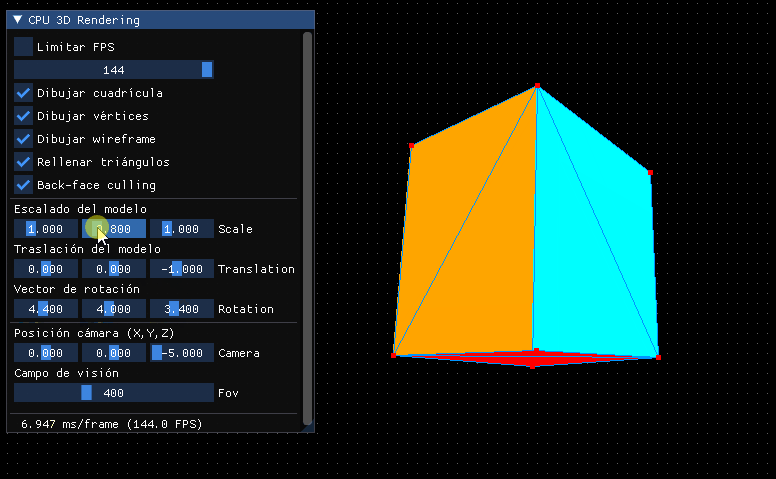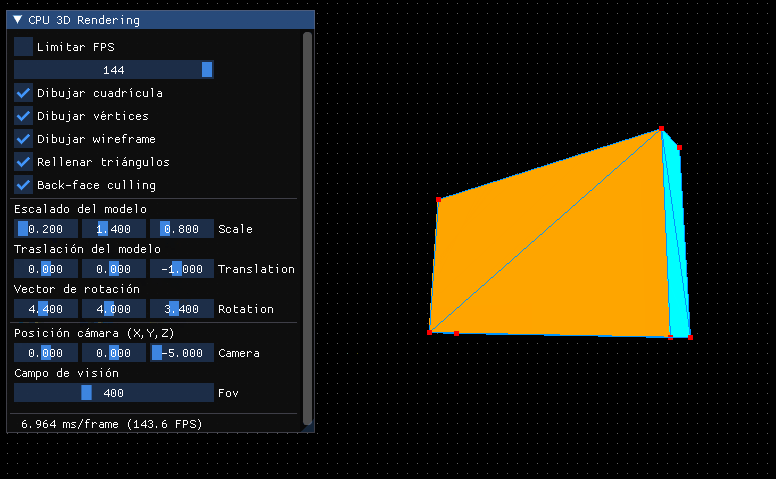
Matriz de mundo 3D¶

La matriz de mundo es una combinación de todas las demás transformaciones (escalado, rotación, traslación...) en una sola matriz.

En la práctica es una multiplicación de todas las demás matrices:

$\begin{bmatrix}m_{11} & m_{12} & m_{13} & m_{14} \\m_{21} & m_{22} & m_{23} & m_{24} \\m_{31} & m_{32} & m_{33} & m_{34} \\m_{41} & m_{42} & m_{43} & m_{44} \\\end{bmatrix}{\color{Red} *}\begin{bmatrix}m_{11} & m_{12} & m_{13} & m_{14} \\m_{21} & m_{22} & m_{23} & m_{24} \\m_{31} & m_{32} & m_{33} & m_{34} \\m_{41} & m_{42} & m_{43} & m_{44} \\\end{bmatrix}$

Necesitaremos implementar la multiplicación de dos matrices Matrix4 aplicando las reglas de multiplicación sobrecargando operadores:

Matrix4 operator*(Matrix4 m2) const
{
    Matrix4 result;
    for (size_t i = 0; i < 4; i++)
    {
        for (size_t j = 0; j < 4; j++)
        {
            result.m[i][j] = m[i][0] * m2.m[0][j] +
                                m[i][1] * m2.m[1][j] +
                                m[i][2] * m2.m[2][j] +
                                m[i][3] * m2.m[3][j];
        }
    }
    return result;
}

Como este método para generar la matriz de mundo es global recibirá la escala, ángulo y traslación.

Es extremadamente importante respetar el orden de multiplicación de matrices, recodemos que AxB != BxA y aquí debemos multiplicar siempre primero por la matriz de transformación. Por supuesto también debemos respetar el orden: primero escalar, luego rotar y finalmente trasladar:

static Matrix4 WorldMatrix(Vector3 scale, Vector3 angle, Vector3 translate)
{
    Matrix4 worldMatrix = Matrix4::IdentityMatrix();
    /* El orden de la multiplicación importa ROTACIOn * MUNDO */
    worldMatrix = Matrix4::ScalationMatrix(scale.x, scale.y, scale.z) * worldMatrix;
    worldMatrix = Matrix4::RotationXMatrix(angle.x) * worldMatrix;
    worldMatrix = Matrix4::RotationYMatrix(angle.y) * worldMatrix;
    worldMatrix = Matrix4::RotationZMatrix(angle.z) * worldMatrix;
    worldMatrix = Matrix4::TranslationMatrix(translate.x, translate.y, translate.z) * worldMatrix;
    return worldMatrix;
}

Haremos la llamada de la función desde Triangle en un nuevo método WorldVertex:

void WorldVertex(int vertexIndex, Vector3 scale, Vector3 angle, Vector3 translate)
{
    // Use a matrix to world transform the origin vertex
    Vector4 transformedVertex{vertices[vertexIndex]};
    transformedVertex = transformedVertex * Matrix4::WorldMatrix(scale, angle, translate);
    vertices[vertexIndex] = transformedVertex.ToVector3();
}

Con esto tendremos la matriz de mundo todo en una:

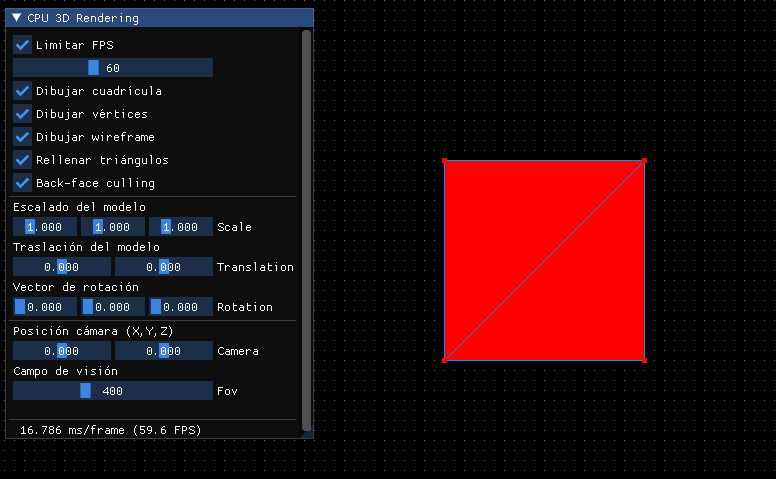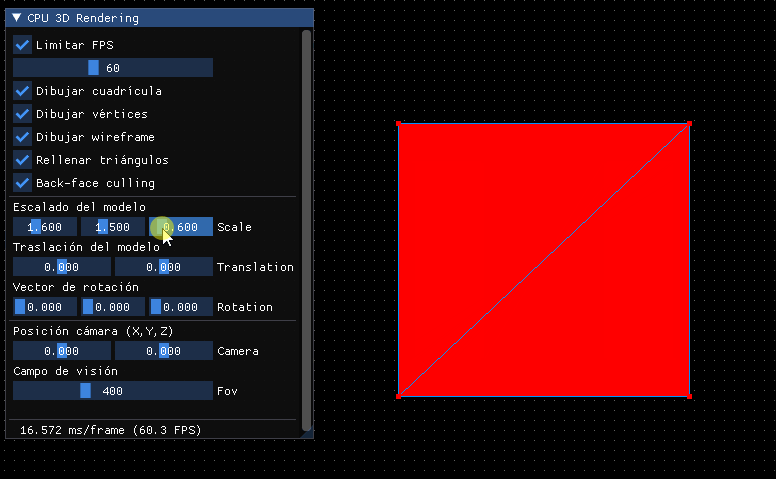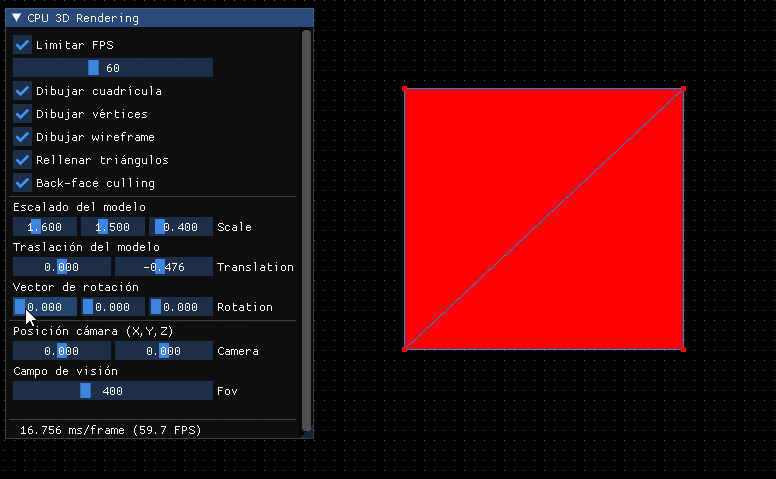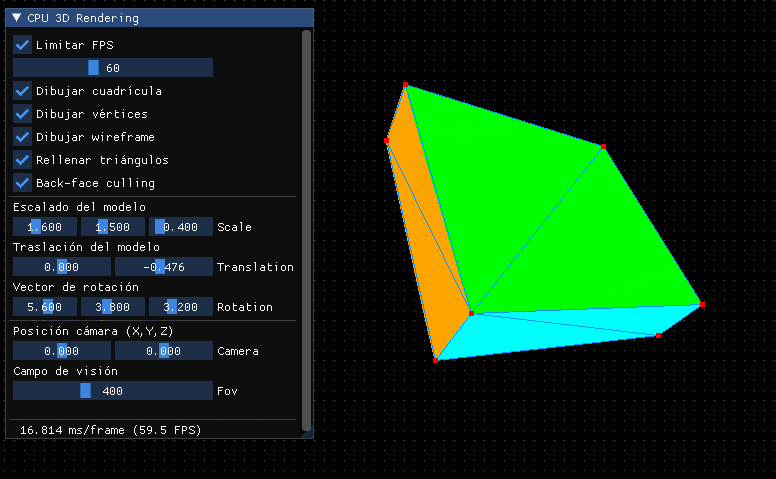
Reflexión sobre la traslación¶

Según lo tratado hasta ahora, la traslación es una transformación un tanto especial, recordemos que es la única que requiere la cuarta columna para multiplicar los valores por la cantidad de traslación:

$\begin{bmatrix}1&0&0&{\color{Blue}tx}\\0&1&0&{\color{Blue}ty}\\0&0&1&{\color{Blue}tz}\\0&0&0&1\\\end{bmatrix}{\color{Red}*}\begin{bmatrix}x\\y\\z\\1\\\end{bmatrix}$

La realidad es que la traslación no es una transformación lineal, ya que estas deben cumplir:

Una transformación lineal debe empezar con una línea.
El resultado de una transformación lineal es una línea.
El origen (centro) de la transformación lineal no puede cambiar.

A diferencia del escalado y la rotación, que se realizan respecto al centro del objeto (0,0), la traslación es una operación que requiere cambiar la posición y por tanto el centro del objeto cambiará.

Para solucionar este problema lo que hacemos es abstraer el vector a una cuarta dimensión imaginaria (la cuarta columna y fila de la matriz), realizamos los cálculos pertinentes para trasladarlos y una vez lo tenemos transformamos de nuevo al espacio tridimensional 3D.

Última edición: 05 de Junio de 2022