Matriz de proyección¶
Otro aspecto que podemos realizar mediante matrices es la proyección del espacio 3D al espacio 2D, algo que no se limita a una proyección perspectiva, ya que con la matriz adecuada conseguiremos distintos efectos.
Hasta ahora para realizar una proyección utilizábamos la brecha de perspectiva, dividiendo las distancias entre la profundidad para conseguir la representación bidimensional. Esta proyección se considera "débil", ya que solo tiene en cuenta la propia brecha.
Lo que haremos será definir una matriz de proyección mucho más sofisticada sobre la que aplicar la brecha de perspectiva:
- Implementará la relación de aspecto para los valores
xeyen función del ancho y alto de la pantalla. - Implementará la campo de visión para los valores
xeyen función del ángulo FOV. - Implementará la normalización para los valores
x,y,zentre-1y1.
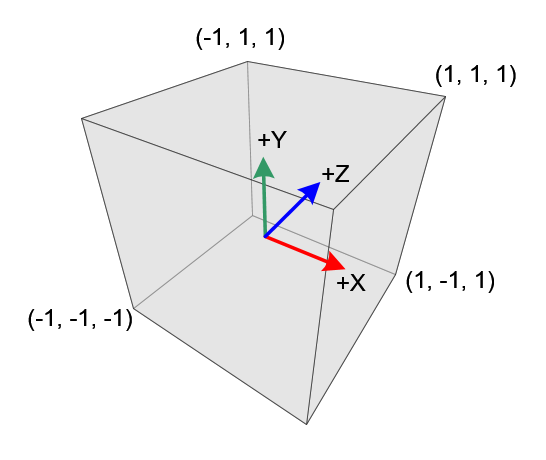
Al tener en cuenta todos estos parámetros, conseguiremos un cubo de valores normalizados, una imagen del espacio (image space) o NDC (Normalized Device Coordinates):
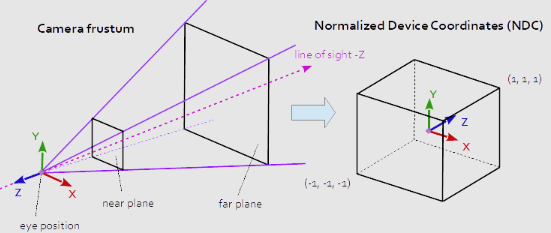
Empecemos por el principio, la relación de aspecto a es la relación entre la altura h (height) y anchura w (width) de la pantalla.
Para conseguir la conversión del espacio de mundo (world space) a espacio de pantalla (screen space) adaptaremos el ancho x multiplicándolo por la relación de aspecto:
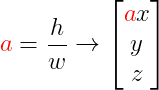
En cuanto al campo de visión nos requerirá encontrar un factor de escalado. Este lo podemos encontrar mediante la relación entre el cateto opuesto y el adjunto, es decir, la mitad de la tangente (el cateto opuesto mide la mitad):
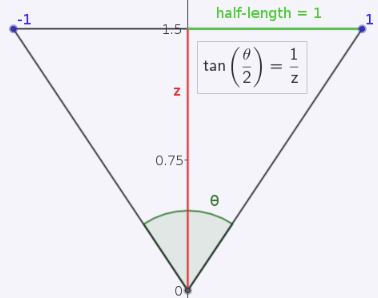
Sin embargo encontramos una contradicción y es que cuanto mayor es el ángulo, más elementos vemos pero también serán más pequeños en la pantalla. Por contra, cuanto menor es el ángulo, menos elementos veremos pero serán más grandes en la pantalla. Por esa razón la función que buscamos es opuesta a la tangente de la mitad del ángulo:
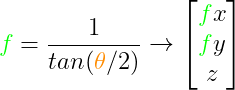
Lo último que necesitamos aplicar es la normalización del espacio visualizado, para ello buscaremos otro factor de escalado. Delimitaremos la profundidad del Frustum entre la Z más alejada zfar y la Z más cercana znear.
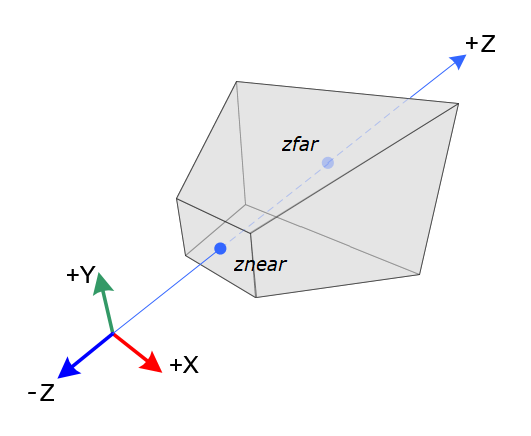
Podemos llamar al factor de escalado simplemente λ, será la distancia máxima zfar entre la diferencia entre zfar y znear:
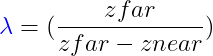
Sin embargo debemos tener en cuenta el offset de znear, pues ésta no parte de cero:
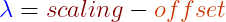
Sustraemos esa distancia inicial, la cuál conseguiremos multiplicando el factor de escalado y znear:
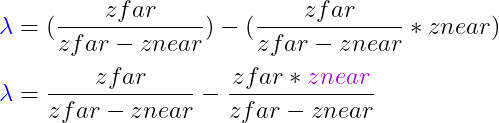
Con esto ya tenemos los factores de la relación de aspecto, el campo de visión y la normalización de la profundidad:
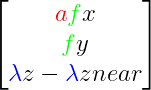
Si los aplicamos antes de la brecha de perspectiva (x/z, y/z, z/z) obtendremos la imagen del espacio normalizado:
Si trasladamos todos los factores a nuestra matriz de referencia 4x4 conseguiremos la matriz de proyección:
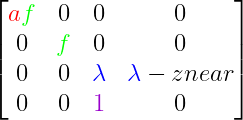
Esta es la matriz de proyección pero sin tener en cuenta la brecha de perspectiva.
Por cierto, veremos un número 1 en la cuarta fila y tercera columna. Al aplicar la multiplicación de matrices nos permitirá guardar el valor original de Z en W, es decir un backup del valor Z sin normalizar. Necesitaremos este valor para aplicar la brecha de perspectiva y también nos hará falta en el futuro para realizar diferentes operaciones.
En cualquier caso necesitaremos implementar dos métodos en Matrix4, uno para definir la matriz de perspectiva:
static Matrix4 PerspectiveMatrix(float fov, float aspect, float znear, float zfar)
{
// | (h/w)*1/tan(fov/2) 0 0 0 |
// | 0 1/tan(fov/2) 0 0 |
// | 0 0 zf/(zf/zn) (-zf*zn)/(zf-zn) |
// | 0 0 1 0 |
Matrix4 m = {{{0}}};
m.m[0][0] = aspect * (1 / tan(fov / 2));
m.m[1][1] = 1 / tan(fov / 2);
m.m[2][2] = zfar / (zfar - znear);
m.m[2][3] = (-zfar * znear) / (zfar - znear);
m.m[3][2] = 1.0;
return m;
}
Y otro para aplicarle la brecha de perspectiva y realizar la proyección:
static Vector4 ProjectMatrix(Matrix4 perspectiveMatrix, Vector4 originalVector)
{
// Multiplicar la matriz de proyección por el vector original
Vector4 result = originalVector * perspectiveMatrix;
// Realizar la brecha de perspectiva con el valor original de z guardado en w
if (result.w != 0.0)
{
result.x /= result.w;
result.y /= result.w;
result.z /= result.w;
}
return result;
}
Para hacer uso de esta nueva funcionalidad tendremos que sustituir el código de proyección anterior, empezando por definir la configuración de la matriz de perspectiva. Podemos definirla inicialmente en window.h:
/* Projection settings */
float fovFactor = M_PI / 3.0; // 60º in radians
float aspectRatio = windowHeight / static_cast<float>(windowWidth);
float zNear = 0.1, zFar = 20.0;
Matrix4 projectionMatrix = Matrix4::PerspectiveMatrix(fovFactor, aspectRatio, zNear, zFar);
Ahora realizaremos la proyección utilizando matrices, para ello utilizaremos un nuevo método triangle.ProjectWorldVertex:
/*** Apply projections for all face vertices ***/
for (size_t j = 0; j < 3; j++)
{
// Project the current vertex using matrices
triangles[i].ProjectWorldVertex(j, window->projectionMatrix);
// Translate the projected vertex to the middle screen
triangles[i].projectedVertices[j].x += (window->windowWidth / 2);
triangles[i].projectedVertices[j].y += (window->windowHeight / 2);
}
Este método cambiará algunas cosas internas respecto al antiguo, empezando por el hecho de que ahora los vértices proyectados serán un Vector4 en lugar de un Vector2:
Vector4 projectedVertices[3]; // 2d vertices
void ProjectWorldVertex(int vertexIndex, Matrix4 projectionMatrix)
{
// Use a matrix to world project the original vertex
Vector4 transformedVertex{vertices[vertexIndex]};
projectedVertices[vertexIndex] = Matrix4::ProjectMatrix(projectionMatrix, transformedVertex);
};
Si ejecutamos el programa veremos solo un punto en el centro:

El problema está relacionado con el normalizado del espacio proyectado NDC (Normalized Device Coordinates).
Como todo está en el rango (-1, 1) debemos escalar los vértices proyectados por la mitad del ancho y alto de la pantalla, importante hacerlo antes de la traslación (recordar el orden):
/*** Apply projections for all face vertices ***/
for (size_t j = 0; j < 3; j++)
{
// Project the current vertex using matrices
triangles[i].ProjectWorldVertex(j, window->projectionMatrix);
// First scale the projected vertex by screen sizes
triangles[i].projectedVertices[j].x *= (window->windowWidth / 2.0);
triangles[i].projectedVertices[j].y *= (window->windowHeight / 2.0);
// Then translate the projected vertex to the middle screen
triangles[i].projectedVertices[j].x += (window->windowWidth / 2.0);
triangles[i].projectedVertices[j].y += (window->windowHeight / 2.0);
}
El resultado será el mismo de antes, pero al haber incorporado la relación de aspecto, el punto de vista y la normalización nos dará mucho juego:
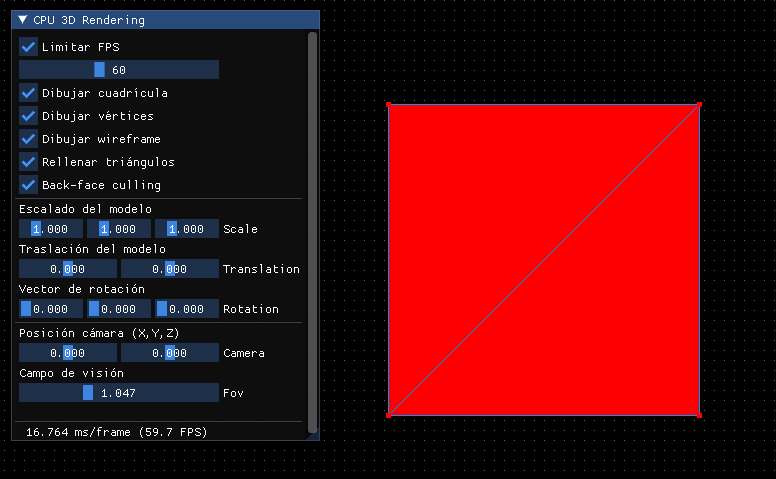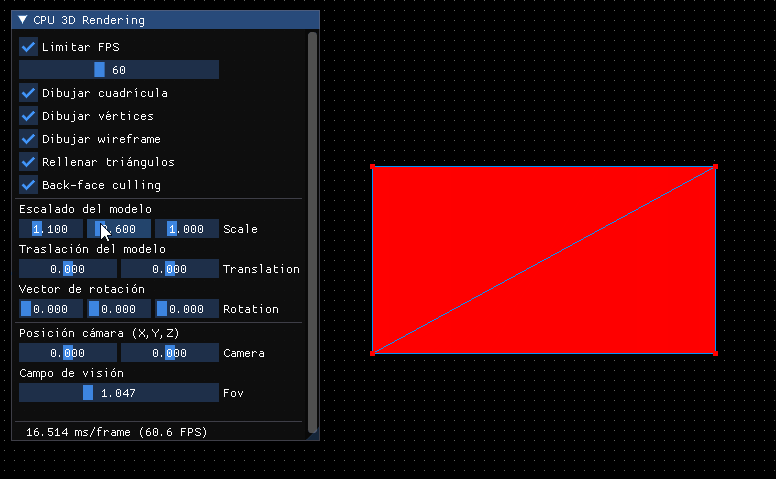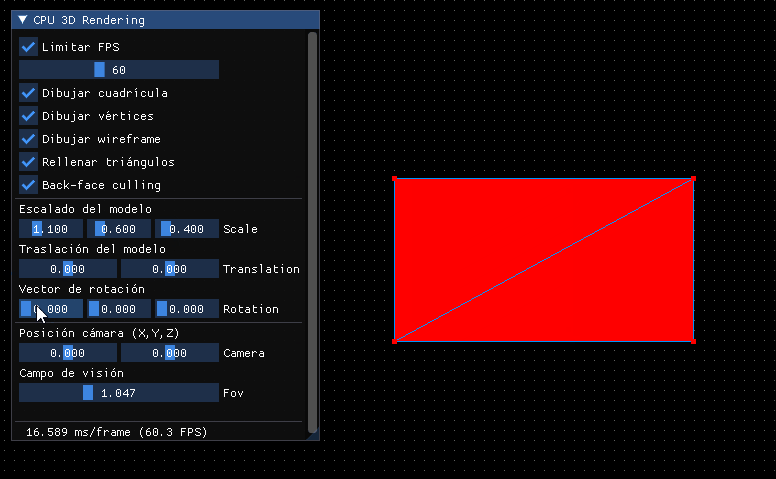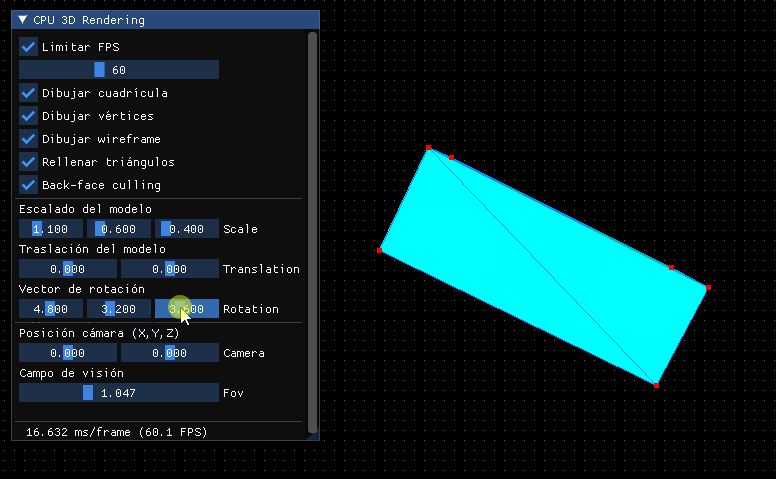
Por lo pronto deberíamos hacer que si se modifica el POV cambie, además de poder establecerlo en grados:
float fovFactor = M_PI / 3.0; // 60º in radians
float fovFactorInGrades = (180.0 / M_PI) * fovFactor; // 60º en grados
ImGui::Text("Campo de visión");
ImGui::SliderFloat("Fov", &this->fovFactorInGrades, 30, 120);
// Update Projection Matrix
projectionMatrix = Matrix4::PerspectiveMatrix(
(this->fovFactorInGrades / 180.0) * M_PI, aspectRatio, zNear, zFar);
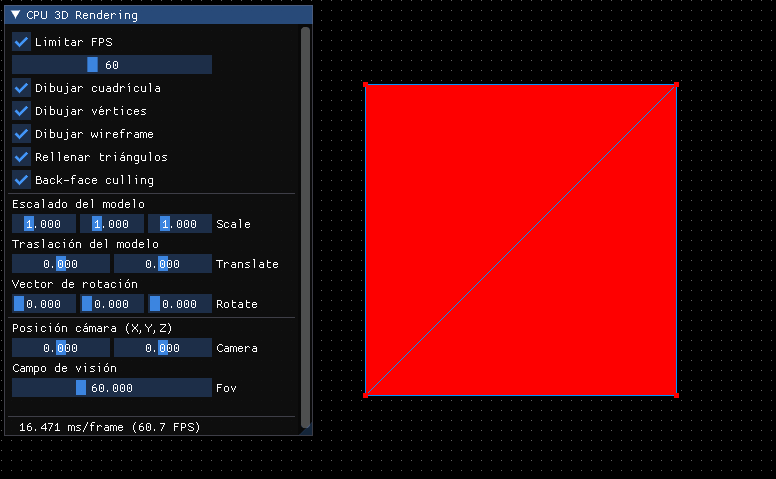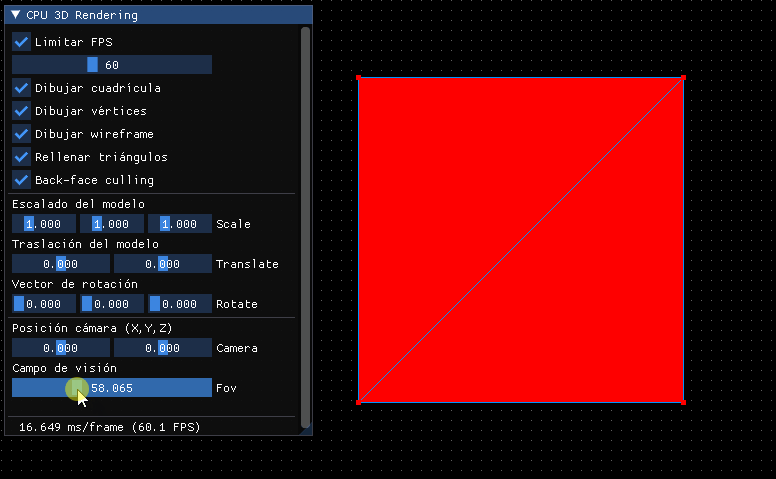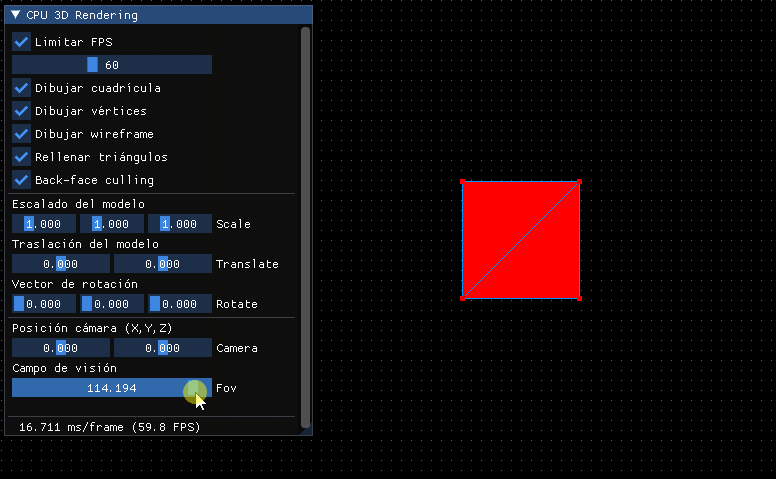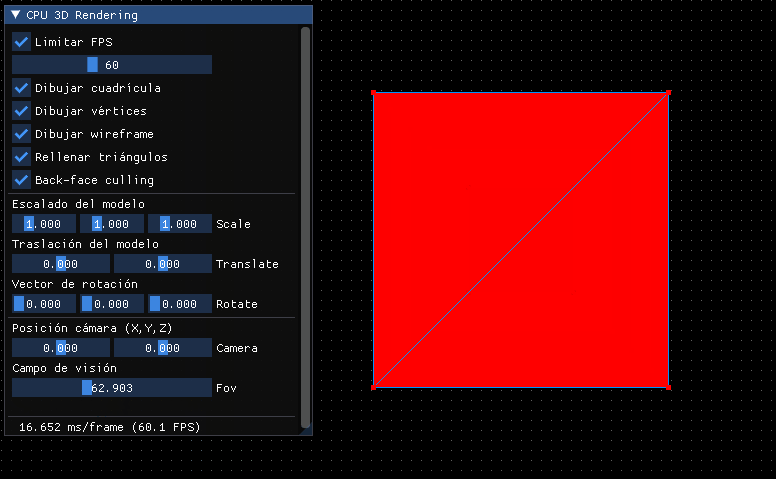
Proyección de valores negativos¶
Ahora que estamos pensando en clave de NDC (Normalized Device Coordinates), podemos cuestionarnos a fondo qué ocurrirá cuando un vector se encuentre proyectado por detrás de la cámara, es decir, que no podamos verlo. ¿Qué tipo de resultado obtendremos?
Al aplicar la brecha de perspectiva:

Al tener en W un componente Z no transformado y potencialmente negativo, el resultado que obtendremos al proyectarlo será una proyeción volteada del objeto como consecuencia de dividir los componentes x, y, z entre un número negativo.
El caso es que antes de que esto ocurra, cuando el objeto se encuentre por detrás de la cámara, el programa se bloqueará y finalizará abruptamente:
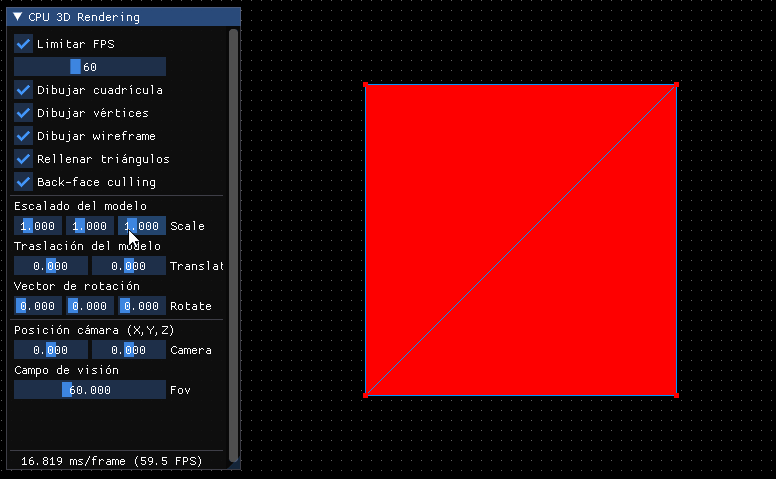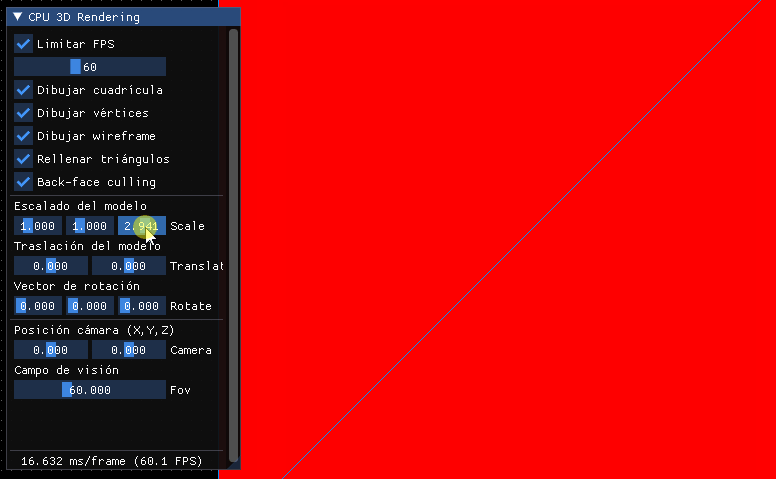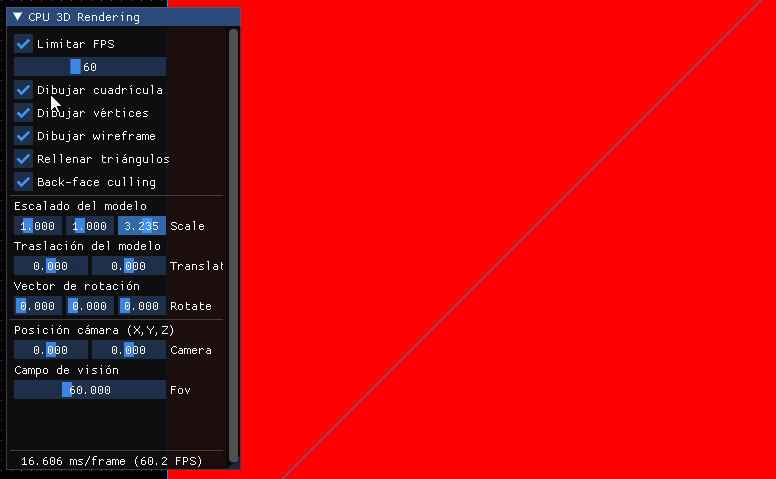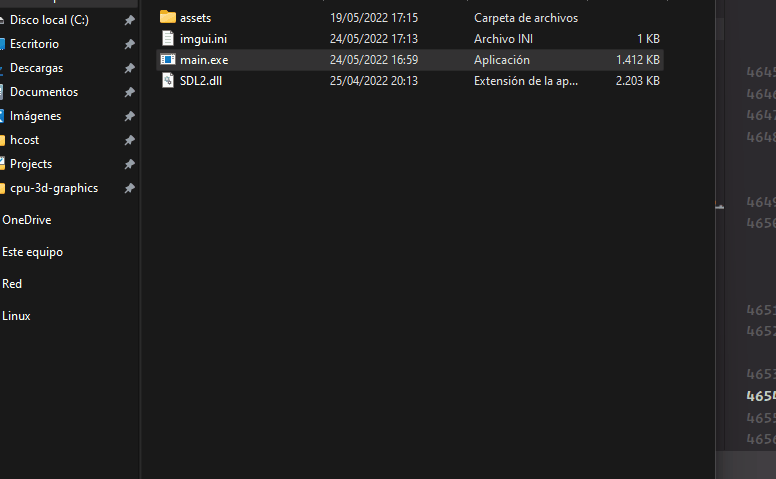
Esto ocurre porque no hemos implementado ningún tipo de protección al intentar dividir los valores entre cero, como sería el clipping, basado en descartar los objetos fuera del frustum para no renderizarlos:
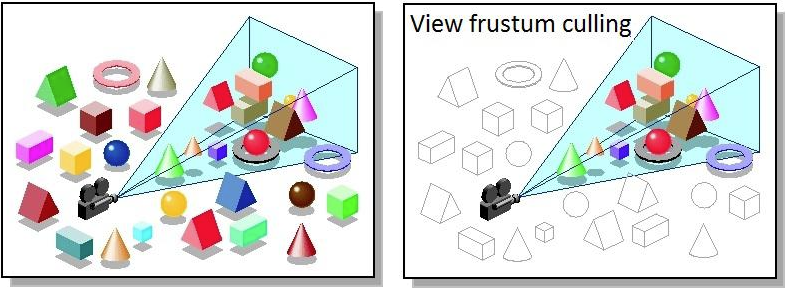
Este proceso tiene lugar normalmente entre la proyección de la matriz y la brecha de perspectiva, por eso es buena idea dividir esas dos operaciones.
En cualquier caso implementaré el clipping más adelante, una vez tenga el terreno preparado.
Orden mayor de fila-columna¶
Antes de continuar, un breve apunte sobre la representación de vectores. Tenemos dos formas de representarlos.
Por orden mayor de columna:

O por orden mayor de fila:
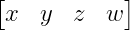
Es importante porque este cambio en la representación no es solo estético, pues hablando de dimensiones no es lo mismo 4x1 que 4x1, algo que afecta directamente a operaciones como la multiplicación de matrices:
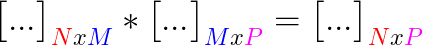
Pues no cumplen la propiedad conmutativa:

Hay que tenerlo en cuenta pues no es lo mismo trabajar con OpenGL que utiliza orden mayor de columna, que con DirectX o programas como Maya que utilizan orden mayor de fila.
Con orden mayor de columna el vector se opera después de la matriz:
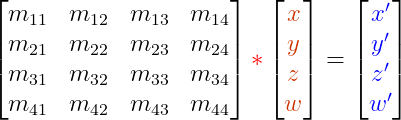
Con orden mayor de fila el vector se opera antes de la matriz:
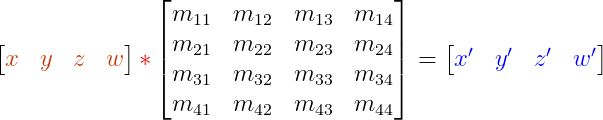
Esto afecta directamente a la configuración de las matrices de transformación y el orden:
- Orden mayor de fila:
P' = P * Ry * Rz * T - Orden mayor de columna:
P' = T * Rz * Ry * P
Distintas formas de interpretar el mundo, distintas formas de trabajar en él, no lo olvidemos.
Última edición: 05 de Junio de 2022
