Profundidad con Z-Buffer¶

En estos momentos estamos controlando la profundidad realizando una media entre los vértices de un triángulo.

En lugar de aplicar la profunidad a nivel de triángulo debemos calcularla para cada píxel que se va a renderizar y para ello haremos uso de la técnica del Z-Buffer, también llamado buffer de profundidad.

Como su nombre indica se basa en crear una array del tamaño de píxeles de la pantalla y almacenar en él la profundidad para cada uno de ellos.

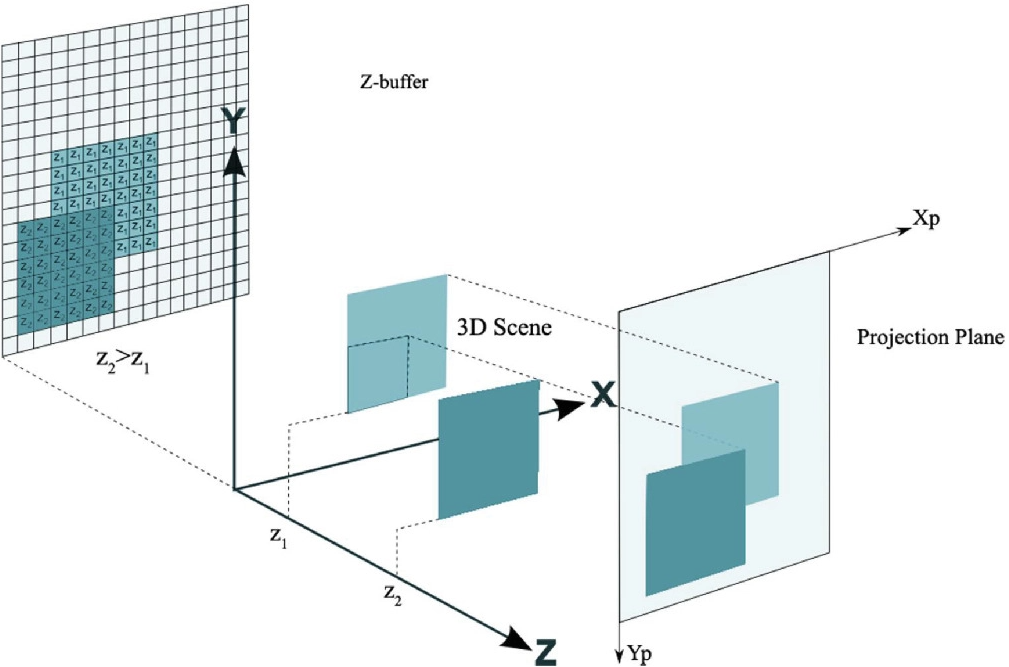
Mediante un zbuffer podemos dibujar correctamente situaciones que el algoritmo del pintor no es capaz de manejar:

A menudo se representa con valores en escala de grises. Los colores brillantes y oscuros son opuestos en cercanía y lejanía o viceversa, dependiendo de lo que se decida:

El caso es que como los valores interpolados de Z no son lineales en el triángulo no los podemos utilizar para almacenar la profundidad. ¿Qué utilizaremos entonces? Pues el recíproco de la profundidad 1/W que tenemos guardado. De hecho podríamos llamarlo W-Buffer.

En cualquier caso para implementar este buffer vamos a crearlo a la par que el colorBuffer pero público para tener acceso en otras clases:

public:
    /* Depth buffer  */
    float* depthBuffer{ nullptr };

Reservamos la memoria en el Window::Setup:

// Reservar la memoria para el depth buffer
depthBuffer = static_cast<float*>(malloc(sizeof(float) * windowWidth * windowHeight));

Liberamos la memoria en el destructor Window::~Window:

// Liberar la memoria dinámica
free(depthBuffer);

Luego, lo que haremos es limpiar el buffer casi al final del renderizado, justo antes de SDL_RenderPresent:

// Clear depth buffer before rendeer present
ClearDepthBuffer();

Así que vamos a crear el método ClearDepthBuffer:

void Window::ClearDepthBuffer()
{
    for (size_t y = 0; y < windowHeight; y++)
    {
        for (size_t x = 0; x < windowWidth; x++)
        {
            depthBuffer[(windowWidth * y) + x] = 1.0;
        }
    }
}

La profundidad inicial de cada píxel será 1.0 porque actualizaremos el valor al detectar otro píxel con un valor menor que el actual, y que al estar normalizado siempre será un valor entre 0 y 1.

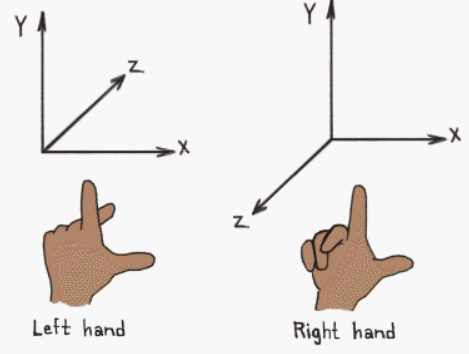
Esto es por el hecho de que en nuestro sistema la Z crece hacia dentro de la pantalla y cuanto menor sea más cerca estará (está basado en la regla de la mano izquierda):

Una vez dibujamos un píxel de la textura en DrawTexel, justo al final de todo, actualizaremos la profundidad de ese píxel en el depthBuffer:

void Window::DrawTexel(Window *window, //...
{
    // And update the depth for the pixel in the depthBuffer
    this->depthBuffer[(this->windowWidth * y) + x] = interpolatedReciprocalW;
}

La verdadera magia viene en este momento, solo dibujaremos el pixel si su profundidad es menor que la que tenemos almacenada ya en el depthBuffer:

// Only draw the pixel if the depth value is less than the one previously stored in the depth buffer
if (interpolatedReciprocalW < this->depthBuffer[(this->windowWidth * y) + x])
{
    // Finally draw the pixel with the color stored in our texture harcoded array
    DrawPixel(x, y, texture[(textureWidth * texelY) + texelX]);

    // And update the depth for the pixel in the depthBuffer
    this->depthBuffer[(this->windowWidth * y) + x] = interpolatedReciprocalW;
}

Solo nos falta un pequeño ajuste y es que debemos tener en cuenta que según nuestros cálculos cuanto más lejos de la cámara se encuentra un punto más pequeña es su profundidad recíproca 1/W, debemos recordar que se encuentra invertida.

Sin embargo nuestra lógica es actualizar el buffer cuando la profundidad esté más cerca (siendo 1.0 el valor inicial), así que debemos ajustar el valor para que sea la distancia contraria, por ejemplo en lugar de 0.1 sea 0.9, justo antes de la condición:

// Adjust the reciprocal 1/w to the contrary distance 
interpolatedReciprocalW = 1 - interpolatedReciprocalW;

if (interpolatedReciprocalW < this->depthBuffer[(this->windowWidth * y) + x]) // ...

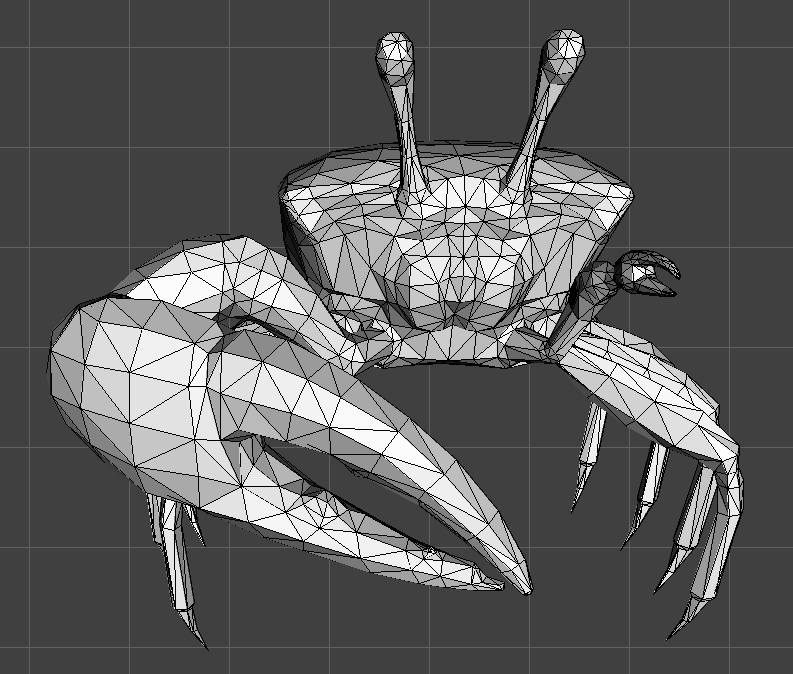
Con esto tendremos el buffer de profundidad funcionando perfectamente y las pinzas del cangrejo ya no se verán por delante:

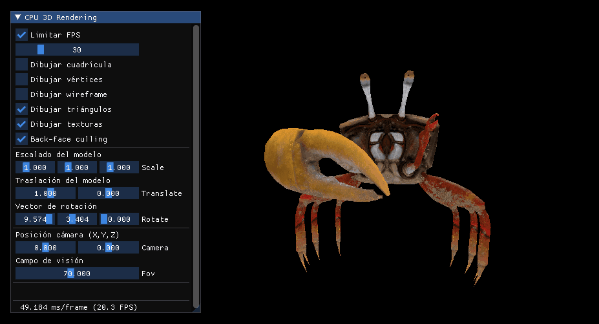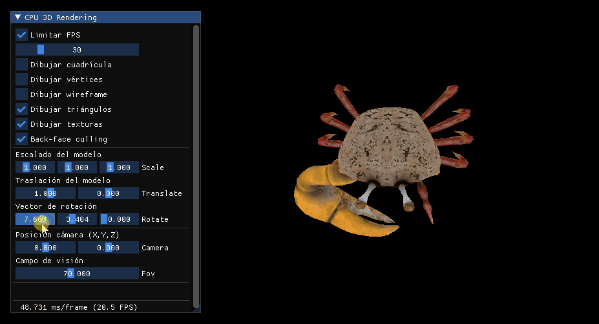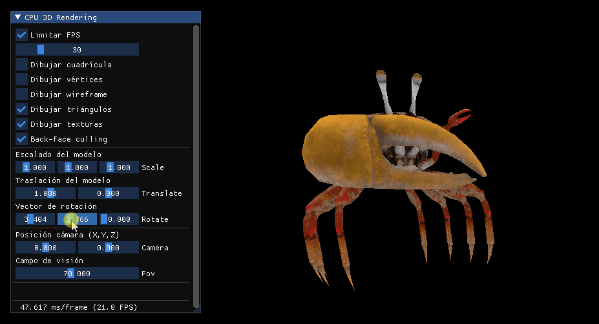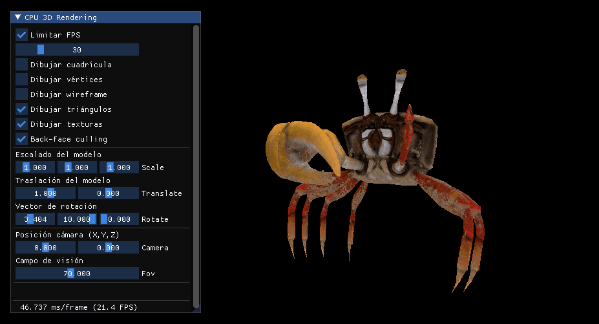
Y ya lo tenemos, aunque personalmente todavía añadiría una pequeña comprobación para no dibujar fuera del tamaño de los buffers:

// Security check to not draw outside the buffers size
int bufferPosition = this->windowWidth * y + x;
if (bufferPosition >= 0 && bufferPosition <= (this->windowWidth * this->windowHeight)) {
    // Only draw the pixel if the depth value is less than the one previously stored in the depth buffer
    if (interpolatedReciprocalW < this->depthBuffer[(this->windowWidth * y) + x])
    {
        // Finally draw the pixel with the color stored in our texture harcoded array
        DrawPixel(x, y, texture[(textureWidth * texelY) + texelX]);

        // And update the depth for the pixel in the depthBuffer
        this->depthBuffer[(this->windowWidth * y) + x] = interpolatedReciprocalW;
    }
}

Esto es un pequeño parche, lo interesante de verdad es la implementación del culling para descartar el dibujado de los triángulos fuera del frustum.

Buffer de profundidad con triángulos¶

Voy a adaptar la función DrawTexturedTriangle para que también tenga en cuenta la profundidad en DrawFilledTriangle, tenemos que borrar las partes que hacen uso de las texturas:

void Window::DrawFilledTriangle(int x0, int y0, float z0, float w0, int x1, int y1, float z1, float w1, int x2, int y2, float z2, float w2, uint32_t color)
{
    // Iterar todos los píxeles del triángulo para renderizarlos en función del color de la textura
    if (y0 > y1) // Primer intercambio
    {
        SwapIntegers(&y0, &y1);
        SwapIntegers(&x0, &x1);
        SwapFloats(&z0, &z1);
        SwapFloats(&w0, &w1);
    }
    if (y1 > y2) // Segundo intercambio
    {
        SwapIntegers(&y1, &y2);
        SwapIntegers(&x1, &x2);
        SwapFloats(&z1, &z2);
        SwapFloats(&w1, &w2);
    }
    if (y0 > y1) // Tercer intercambio
    {
        SwapIntegers(&y0, &y1);
        SwapIntegers(&x0, &x1);
        SwapFloats(&z0, &z1);
        SwapFloats(&w0, &w1);
    }

    // Create vector4 points
    Vector4 pA{ (double)x0, (double)y0, (double)z0, (double)w0 };
    Vector4 pB{ (double)x1, (double)y1, (double)z1, (double)w1 };
    Vector4 pC{ (double)x2, (double)y2, (double)z2, (double)w2 };

    // Common divisions for depth calculations
    float oneDivW[3] = { 1 / pA.w , 1 / pB.w, 1 / pC.w };

    /*** Render the upper part of the triangle (flat bottom) ***/
    {
        float m1 = 0;
        float m2 = 0;

        // Checks to avoid infinite divisions
        if (y1 - y0 != 0) m1 = -((y1 - y0) / static_cast<float>((x0 - x1))); // m1 izquierda -
        if (y2 - y0 != 0) m2 = (y2 - y0) / static_cast<float>((x2 - x0));    // m2 derecha +
        if (y1 - y0 != 0)
        {

            for (size_t i = 0; i < (y1 - y0); i++)
            {
                int xStart = x0 + (i / m1);
                int xEnd = x0 + (i / m2);
                int y = y0 + i;

                // Sometimes we have to draw the triangle from right to left
                // so we have to swap the xStart and the xEnd
                if (xEnd < xStart) SwapIntegers(&xEnd, &xStart);

                for (int x = xStart; x < xEnd; x++)
                {
                    DrawTrianglePixel(x, y, pA, pB, pC, oneDivW, color);
                }
            }
        }
    }

    /*** Render the lower part of the triangle (flat top) ***/
    {
        float m1 = 0;
        float m2 = 0;
        // Checks to avoid infinite divisions
        if (y2 - y1 != 0) m1 = -((y2 - y1) / static_cast<float>((x2 - x1))); // m1 izquierda -
        if (y2 - y0 != 0) m2 = -((y2 - y0) / static_cast<float>((x2 - x0))); // m2 izquierda -
        if (y2 - y1 != 0)
        {
            for (size_t i = 0; i <= (y2 - y1); i++)
            {
                int xStart = x2 + (i / m1);
                int xEnd = x2 + (i / m2);
                int y = y2 - i;

                // Sometimes we have to draw the triangle from right to left
                // so we have to swap the xStart and the xEnd
                if (xEnd < xStart) SwapIntegers(&xEnd, &xStart);

                for (int x = xStart; x < xEnd; x++)
                {
                    DrawTrianglePixel(x, y, pA, pB, pC, oneDivW, color);
                }
            }
        }
    }
}

En lugar de DrawTexel definiremos una variante que no tenga en cuenta texturas ni coordenadas UV llamada DrawTrianglePixel:

void Window::DrawTrianglePixel(int x, int y, Vector4 a, Vector4 b, Vector4 c, float* oneDivW, uint32_t color)
{
    // Create p vector with current pixel location
    Vector2 p{ static_cast<double>(x),static_cast<double>(y) };
    // Calculate the weights using the vectors A,B,C and P
    Vector3 weights = Vector3::BarycentricWeights(a.ToVector2(), b.ToVector2(), c.ToVector2(), p);
    float alpha = weights.x;
    float beta = weights.y;
    float gamma = weights.z;

    // Variables to store the interpolated values of U, V and also the reciprocal 1/w for the current pixel
    float interpolatedReciprocalW;

    // Find the interpolate value of 1/w for the current pixel
    interpolatedReciprocalW = oneDivW[0] * alpha + oneDivW[1] * beta + oneDivW[2] * gamma;

    // Adjust the reciprocal 1/w to the contrary distance. E.g. 0.1 -> 0.9
    interpolatedReciprocalW = 1 - interpolatedReciprocalW;

    // Security check to not draw outside the buffers size
    int bufferPosition = this->windowWidth * y + x;
    if (bufferPosition >= 0 && bufferPosition <= (this->windowWidth * this->windowHeight)) {
        // Only draw the pixel if the depth value is less than the one previously stored in the depth buffer
        if (interpolatedReciprocalW < this->depthBuffer[(this->windowWidth * y) + x])
        {
            // Finally draw the pixel with the solid color
            DrawPixel(x, y, color);

            // And update the depth for the pixel in the depthBuffer
            this->depthBuffer[(this->windowWidth * y) + x] = interpolatedReciprocalW;
        }
    }
}

Con esto ya tendremos los triángulos sin texturas rasterizados con profundidad:

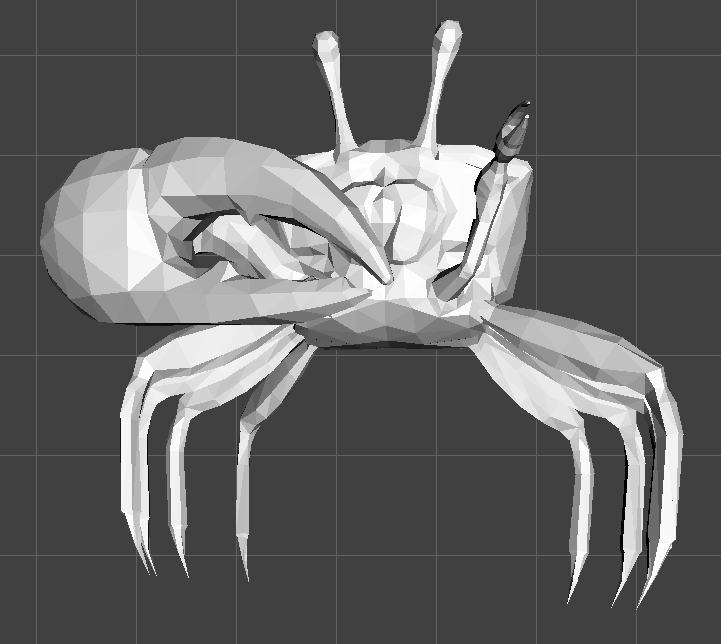
Ya no necesitamos calcular la profundidad media ni ordenar los triángulos:

void Mesh::Update()
{
    /* Before project calculate depth */
    // triangles[i].CalculateAverageDepth();
}

void Mesh::Render()
{
    // Antes de renderizar triángulos ordenarlos 
    // Esto ya no es necesario al estar utilizando un zbuffer
    // std::deque<Triangle> sortedTriangles(triangles);
    // std::sort(sortedTriangles.begin(), sortedTriangles.end());
}

Tendremos que cambiar todas las referencias a los triángulos ordenados sortedTriangles de nuevo por triangles a secas.

Rasterizado de líneas 3D¶

El problema que tenemos actualmente es que las líneas no tienen en cuenta la profundidad y el wireframe se ve muy raro:

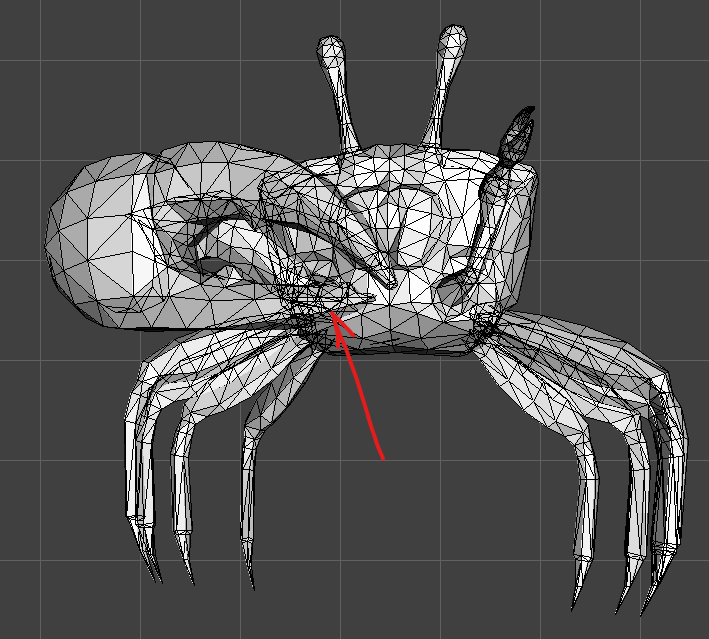
¿Qué tal si también creamos un método que permita dibujar líneas con profundidad? O lo que es lo mismo, líneas 3D. Podemos crear una nueva versión DrawTriangle3D:

void Window::DrawTriangle3D(int x0, int y0, float w0, int x1, int y1, float w1, int x2, int y2, float w2, uint32_t color)
{
    DrawLine3D(x0, y0, w0, x1, y1, w1, color);
    DrawLine3D(x1, y1, w1, x2, y2, w2, color);
    DrawLine3D(x2, y2, w2, x0, y0, w0, color);
}

Ésta llamará a DrawLine3D a la que enviaremos la profundidad en W:

void Window::DrawLine3D(int x0, int y0, float w0, int x1, int y1, float w1, uint32_t color)
{
    // Calculamos la distancia entre X, Y y la recíproca de W
    float deltaX = x1 - x0;
    float deltaY = y1 - y0;
    int deltaReciprocalW = 1.f / w1 - 1.f / w0;

    // Si no hay distancia no hace falta dibujar nada
    if (abs(deltaX) == 0 && abs(deltaY) == 0) return;

    // Buscamos que lado es mayor, el ancho o el alto
    int longestSideLength = abs(deltaX / deltaY) > 1 ? abs(deltaX) : abs(deltaY);

    // Calculamos el incremento por píxel para X, Y y la recíproca de W
    float xInc = deltaX / longestSideLength;
    float yInc = deltaY / longestSideLength;
    float wInc = deltaReciprocalW / static_cast<float>(longestSideLength);

    // Dibujamos todos los puntos para el lado más largo
    for (size_t i = 0; i <= longestSideLength; i++)
    {
        int x = roundf(x0 + (xInc * i));
        int y = roundf(y0 + (yInc * i));
        float oneOverW = 1.0 / (w0 + (wInc * i));
        float zInterpolated = 1.0f - oneOverW;

        // Security check
        int bufferPosition = (windowWidth * y) + x;
        if (bufferPosition >= 0 && bufferPosition <= (this->windowWidth * this->windowHeight)) {
            // Si el valor en Z es menor que el del bufer es que está más cerca
            if (zInterpolated < depthBuffer[bufferPosition])
            {
                DrawPixel(x, y, color);
                depthBuffer[bufferPosition] = zInterpolated;
            }
        }
    }
}

Y dibujamos el wireframe con nuestro nuevo método:

// Wireframe
if (window->drawWireframe)
{
    window->DrawTriangle3D(
        triangles[i].projectedVertices[0].x, triangles[i].projectedVertices[0].y, triangles[i].projectedVertices[0].w,
        triangles[i].projectedVertices[1].x, triangles[i].projectedVertices[1].y, triangles[i].projectedVertices[1].w,
        triangles[i].projectedVertices[2].x, triangles[i].projectedVertices[2].y, triangles[i].projectedVertices[2].w,
        0xFF000000);
}

En principio con esto las líneas 3D harán uso del buffer de profundidad:

Rasterizado de las normales¶

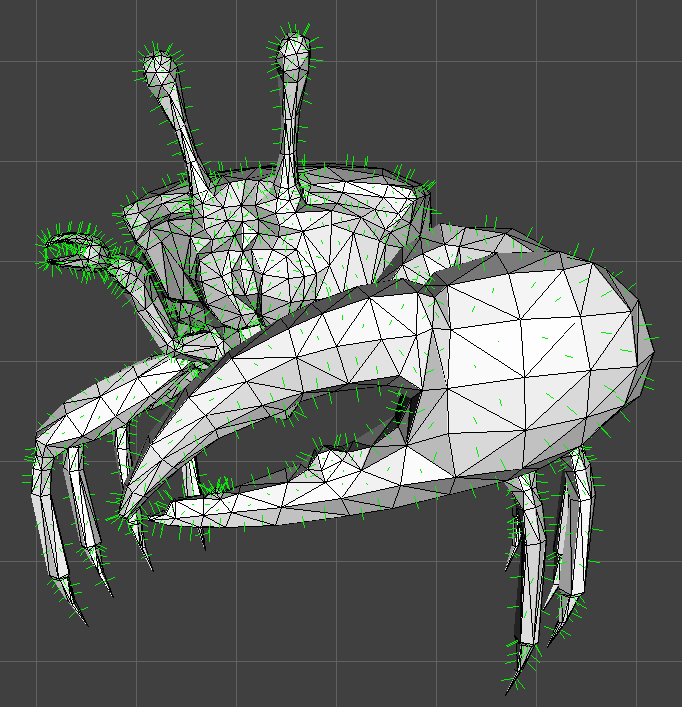
Ahora que contamos con una función para dibujar líneas 3D sería interesante añadir una opción en la interfaz para dibujar las normales de los triángulo y ver su dirección:

class Window
{
public:
    bool drawTriangleNormals = true;
};

ImGui::Checkbox("Dibujar normales", &this->drawTriangleNormals);

Para trazar la normal, que ahora se comportará como otro elemento 3D en la escena, necesitamos:

Decidir el punto de origen y destino en el espacio 3D.
Transformarlos a 2D con la matriz de mundo.
Rectificar las coordenadas proyectados 2D.
Dibujar las líneas 3D pasándoles X, Y y W.

Empecemos por el método para calcular la normal proyectada en Triangle:

class Triangle
{
public:
    Vector3 normal{ 0,0,0 };
    Vector4 projectedNormal[2]{};  // nuevo
};

void ProjectWorldNormal(Matrix4 projectionMatrix)
{
    // Find the middle point of the triangle face to project the normal
    Vector3 midPoint{
        vertices[0].x * 0.3333 + vertices[1].x * 0.3333 + vertices[2].x * 0.3333,
        vertices[0].y * 0.3333 + vertices[1].y * 0.3333 + vertices[2].y * 0.3333,
        vertices[0].z * 0.3333 + vertices[1].z * 0.3333 + vertices[2].z * 0.3333 };
    // Use a matrix to world project the normal vertices
    Vector4 transformedNormalVertex1{ midPoint };
    Vector4 transformedNormalVertex2{ midPoint + normal*0.05 };
    projectedNormal[0] = Matrix4::ProjectMatrix(projectionMatrix, transformedNormalVertex1);
    projectedNormal[1] = Matrix4::ProjectMatrix(projectionMatrix, transformedNormalVertex2);
};

Para calcular el punto medio simplemente he hecho la media de los 3 puntos a modo de coordenada baricéntrica por 0.333 que sería como dividirlos entre 3. La normal partirá de ese punto medio con tamaño de la normal por un factor reducido (está normalizada y 1 sería el máximo).

Durante la actualización del mesh haremos la misma proyección que para cada vértice del triángulo pero para los vértices de la normal con sus debidas rectificaciones:

// Project the normal vectors if we want to draw it
if (window->drawTriangleNormals)
{
    // Project the current normal to create an origin and a destiny vectors
    triangles[i].ProjectWorldNormal(window->projectionMatrix);
    for (size_t j = 0; j < 2; j++)
    {
        // First scale the projected vertex by screen sizes
        triangles[i].projectedNormal[j].x *= (window->windowWidth / 2.0);
        triangles[i].projectedNormal[j].y *= (window->windowHeight / 2.0);
        // Invert the y values to account the flipped screen y coord
        triangles[i].projectedNormal[j].y *= -1;
        // Then translate the projected vertex to the middle screen
        triangles[i].projectedNormal[j].x += (window->windowWidth / 2.0);
        triangles[i].projectedNormal[j].y += (window->windowHeight / 2.0);
    }
}

Finalmente en el renderizado enviaremos a DrawLine3D las coordenadas de inicio y fin de la normal proyectada y rectificada:

// Triangle normals
if (window->drawTriangleNormals)
{
    window->DrawLine3D(
        triangles[i].projectedNormal[0].x, triangles[i].projectedNormal[0].y, triangles[i].projectedNormal[0].w,
        triangles[i].projectedNormal[1].x, triangles[i].projectedNormal[1].y, triangles[i].projectedNormal[1].w,
        0xFF07EB07);
}

El resultado es genial, como las líneas 3D están transformadas y proyectadas se comportan en conjunto con la malla.

Última edición: 05 de Junio de 2022