Matriz de vista y cámaras¶

Este proyecto está prácticamente acabado a falta de implementar una cámara en condiciones para navegar por la escena y la implementación del clipping.

Actualmente estamos manejando dos transformaciones muy importantes mediante dos matrices, una de mundo y otra de proyección. La primera sitúa un objeto en el mundo tridimensional y la segunda transforma ese espacio 3D a uno 2D para visualizarlo en la pantalla. Sin embargo, nuestra idea actual de una cámara, el lugar desde el que estamos observando, es el origen del mundo 3D (0,0,0) y lo que hacemos es llevarnos el mesh al fondo para visualizarlo.

Evidentemente esto no es lo que realmente nos interesa, lo ideal es contar con una cámara de verdad que pueda moverse por la escena y visualizar el conjunto del mundo desde su posición:

Para conseguir este propósito introduciremos lo que se denomina una matriz de vista (view matrix), una transformación que ejecutaremos para establecer el punto de vista desde un lugar concreto. El resultado ya no será el espacio del mundo (world space) sino el espacio de la vista (view space).

En conjunto si repasamos el ciclo de transformaciones tendremos diferentes espacios:

1. En primer lugar los vértices se encuentran en el espacio del modelo, también llamado sistema de coordenadas local y vienen dadas por el propio modelo al crearlo:

   

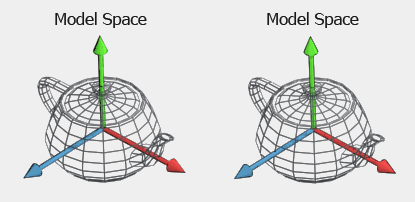
2. A continuación realizamos la transformación de los vértices al espacio del mundo multiplicando el espacio del modelo por la matriz de mundo:

   

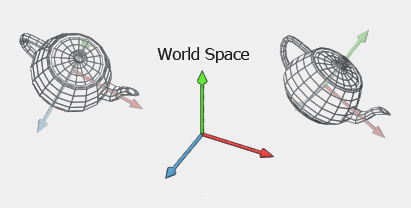
3. El siguiente paso será aplicar la transformación de los vértices al espacio de la vista multiplicando el espacio del mundo por la matriz de vista:

   

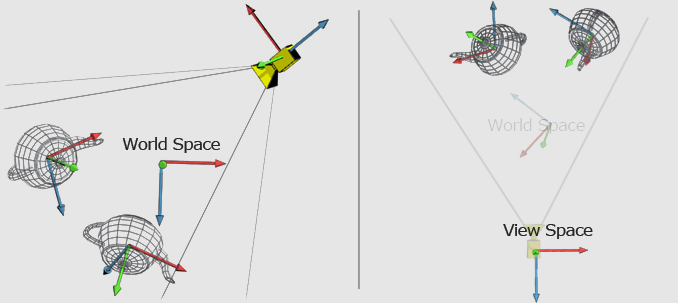
4. Finalmente aplicaremos la transformación de proyección al espacio de la pantalla (screen space) multiplicando el espacio de vista por la matriz de proyección:

   

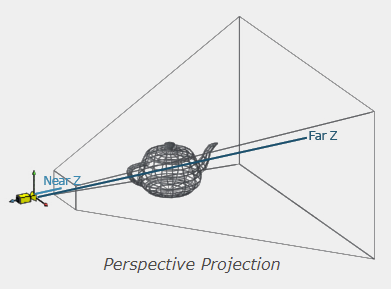
Dependiendo del tipo de cámara que vayamos a implementar aplicaremos una matriz de vista distinta. Por ejemplo, una Look-at Camera es la que mira hacia un lugar concreto, mientras que una cámara de tipo FPS Camera incorpora libertad de movimiento en el espacio.

Empecemos por la cámara hacia un lugar concreto.

Cámara Look-at¶

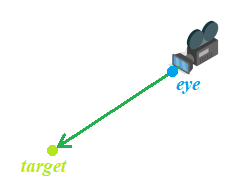
Una de las formas de implementar una view matrix es mediante una función lookAt que retornará una matriz 4x4 utilizada para multiplicar los vértices y convertirlos al view space.

Para establecer la posición y orientación de la cámara en el espacio, se necesita dos puntos:

• El de la posición de la cámara en el espacio (eye point o punto del ojo).
• El de la posición hacia donde está mirando la cámara (target point o punto objetivo).

La transformación lookAt es la responsable de devolver la matriz de la vista (MatrixView) y consta consta de dos transformaciones:

1. Primero la traslación de toda la escena de forma inversa desde la posición del ojo de la cámara hacia el origen (MatrixTranslation).
2. Luego la rotación de la escena con la orientación revertida (MatrixRotation), de manera que la cámara esté posicionada en el origen y mirando al eje Z positivo (por utilizar un sistema basado en la regla de la mano izquierda).

La matriz de la vista será por tanto la combinación de la matriz de rotación y la matriz de traslación:

Ahora debemos determinar cuáles son los elementos a aplicar en ambas matrices, así que vamos a diseccionar las dos transformaciones.

La matriz de traslación es sencilla, solo tenemos que mover la posición de la cámara al origen:

Substituiremos la cuarta columna la matriz de traslación MT por la posición del ojo negado (el sistema está basado en la regla de la mano izquierda):

La matriz de rotación es algo más compleja, debemos empezar computando los vectores (Z adelante, X derecha, Y arriba) de la cámara respecto a donde está mirando:

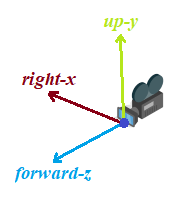
Estos tres vectores (x, y, z) los utilizaremos para construir la matriz de rotación MR:

Sin emargo esta matriz debe estar invertida. ¿Por qué? Si por ejemplo suponemos que la cámara se encuentra por encima de la escena, toda la escena deberá encontrarse rotada hacia abajo. Si se encuentra a la izquierda de la escena, toda la escena deberá encontrarse rotada hacia la izquierda, lo contrario. Por esa razón debemos computar la matriz inversa:

El inverso de un número es aquel que multiplicado por el propio número da como resultado 1:

Con una matriz el concepto es el mismo, solo que en lugar de 1, multiplicar una matriz por su inversa dará como resultado la matriz de identidad:

En la programación gráfica, si tenemos una matriz que rota un elemento por un cierto ángulo, hacer la inversa de esa matriz de rotación hará justo lo contrario, rotar de nuevo el elemento a la posición inicial, es decir, deshacer la operación.

Como decía encontrar la inversa de una matriz es algo bastante tedioso, pero por suerte para nosotros hay un caso donde se simplifica y justamente es el que tenemos en la matriz de rotación MR.

Cuando una matriz es ortogonal, cada fila tiene una longitud de 1 (necesitaremos normalizar los valores) y los valores son mútuamente perpendiculares (podemos invertirlos), para invertirla sólo tenemos que encontrar su matriz transpuesta, que consiste en intercambiar los filas y las columnas:

Así pues, al aplicar todos los valores la matriz de la vista quedará:

Lo cual se puede simplificar mediante productos escalares, en la forma final de nuestra matriz de la vista para una cámara lookAt:

Ahora que tenemos la matriz podemos al fin codificar el método LookAt en la clase Matrix4:

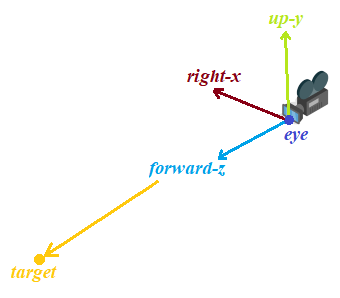
static Matrix4 LookAt(Vector3 eye, Vector3 target, Vector3 up)
{
    // Forward (z) vector in new coordinate system
    Vector3 z = target - eye;
    // Right (x) vector in new coordinate system
    Vector3 x = up.CrossProduct(z);
    // Up (y) vector in new coordinate system
    Vector3 y = z.CrossProduct(x);

    // Normalize the vectors
    x.Normalize();
    y.Normalize();
    z.Normalize();

    // | x.x   x.y   x.z   -dot(x.eye) |
    // | y.x   y.y   y.z   -dot(y.eye) |
    // | z.x   z.y   z.z   -dot(z.eye) |
    // |   0     0     0             1 |

    Matrix4 viewMatrix = {{
        { x.x, x.y, x.z, -x.DotProduct(eye) },
        { y.x, y.y, y.z, -y.DotProduct(eye) },
        { z.x, z.y, z.z, -z.DotProduct(eye) },
        {   0,   0,   0,                  1 },
    }};


    return viewMatrix;
}

Básicamente buscamos los vectores del nuevo sistema de coordenadas y los normalizamos porque solo nos interesa su dirección (teniendo en cuenta que nuestro sistema funciona con la regla de la mano izquierda). Luego construimos la matriz de la vista mediante los vectores y el ojo.

En este punto vamos a modificar el funcionamiento del programa, a partir de ahora ya no tendremos un Vector3 simulando una cámara con el punto origen, sino que la cámara constituirá su propia clase camera.h:

#ifndef CAMERA_H
#define CAMERA_H

#include "vector.h"

class Camera {
public:
    Vector3 position{0,0,0};
};

#endif

De esta cámara crearemos una instancia en window.h, conservaremos el array actual todo a cero para usarlo de interfaz para el slider:

#include "camera.h"

class Window
{
public:
    /* Camera settings */
    float cameraPosition[3] = {0, 0, 0};
    Camera camera;
};

Como ya no utilizaremos cameraPosition le actualizaremos el valor debajo de la interfaz:

// Update Camera Position
camera.position = Vector3(cameraPosition[0], cameraPosition[1], cameraPosition[2]);

Ahora tenemos que adaptar el mesh, empezando por el método SetTranslation:

void Mesh::SetTranslation(float *translation)
{
    // Con rectificación de origen
    this->translation = {
        translation[0] - window->camera.position.x,
        translation[1] - window->camera.position.y,
        translation[2] - window->camera.position.z};
}

Luego en Mesh::Update modificamos el método ApplyCulling para que ahora reciba un puntero a la cámara:

triangles[i].ApplyCulling(&window->camera);

Este método cambiará un poco su lógica respecto a la primera versión, pues ahora asumiremos siempre el punto origen (0,0,0) para calcular el cameraRay (teniendo en cuenta que esto es antes de aplicar la transformación del espacio de la vista):

void ApplyCulling(Camera *camera)
{
    // Setup up the origin 0,0,0 to calculate the initial cameraRay
    Vector3 origin = {0,0,0};
    // Find the vector between a triangle point and camera origin
    Vector3 cameraRay = Vector3(origin - this->vertices[0]);
    // Calculate how aligned the camera ray is with the face normal
    float dotNormalCamera = normal.DotProduct(cameraRay);
    // Test the dotNormalCamera and render the triangle if is >0
    this->culling = (dotNormalCamera < 0);
}

Ahora, justo al principio de cada mesh.Update vamos a crear la matriz viewMatrix de tipo lookAt, por ahora hacia un punto harcodeado.

No es necesaria crear esta matriz en cada ciclo, podemos definirla globalmente en la ventana:

/* Camera settings */
Matrix4 viewMatrix;
float cameraPosition[3] = {0, 0, 0};
Camera camera;

Pero sí que la iremos recalculando en el Update porque si cambia su posición o dirección, todo cambiará :

void Mesh::Update()
{
    // Create a hardcoded target point and the up direction vector
    Vector3 target = { 0, 0, 10 };
    Vector3 upDirection = { 0, 1, 0 };
    // Calculate the view matrix for each frame
    window->viewMatrix = Matrix4::LookAt(window->camera.position, target, upDirection);
}

Justo después de aplicar la transformación de mundo haremos lo propio con la matriz de la vista:

/*** Apply world transformation and view transformation for all face vertices ***/
for (size_t j = 0; j < 3; j++)
{
    // World transformation to get the world space
    triangles[i].WorldVertexTransform(j, scale, rotation, translation);
    // View transformation to get the view space (aka camera space) 
    triangles[i].ViewVertexTransform(j, window->viewMatrix);
}

La implementación será muy sencilla en Triangle:

void ViewVertexTransform(int vertexIndex, Matrix4 viewMatrix)
{
    // Multiply the view matrix by the original vector to transform the scene to camera space
    Vector4 transformedVertex{ vertices[vertexIndex] };
    transformedVertex = transformedVertex * viewMatrix;
    vertices[vertexIndex] = transformedVertex.ToVector3();
}

En este punto ya lo tendremos, pero antes de ejecutar el resultado recordemos que por defecto el modelo se encuentra en el origen (0,0,0). Como hemos establecido nuestra cámara también en (0,0,0) al estar el modelo cortando la cámara es posible que el programa se bloquee o muy muy lento (si la profundidad respecto al ojo tiende a 0 el tamaño resultante es infinito).

Para solucionarlo, primero vamos a rectificar que se reste la cámara de la posición del mesh (ya no nos hace falta):

void Mesh::SetTranslation(float *translation)
{
    // Con rectificación de origen
    this->translation = { translation[0], translation[1], translation[2] };
}

Y simplemente estableceremos la posición del modelo inicialmente a una profundidad de 4 o 5 en window.h:

/* Model settings */
float modelTranslation[3] = {0, 0, 4};

El resultado será el mismo que teníamos antes de utilizar la cámara:

A simple vista no parece una gran mejora pero si actualizamos en cada fotograma el vector target a donde se encuentra el modelo y añadimos un pequeño cambio en la posición de la cámara:

void Mesh::Update()
{
    // Create a hardcoded target point and the up direction vector
    Vector3 target = { 
        window->modelTranslation[0], 
        window->modelTranslation[1], 
        window->modelTranslation[2] };

    // Add a slight movement to the camera to the right
    window->cameraPosition[0] += 0.025;
    window->cameraPosition[1] += 0.025;
    window->cameraPosition[2] -= 0.025;
}

Quedará claro que hemos conseguido algo súmamente importante:

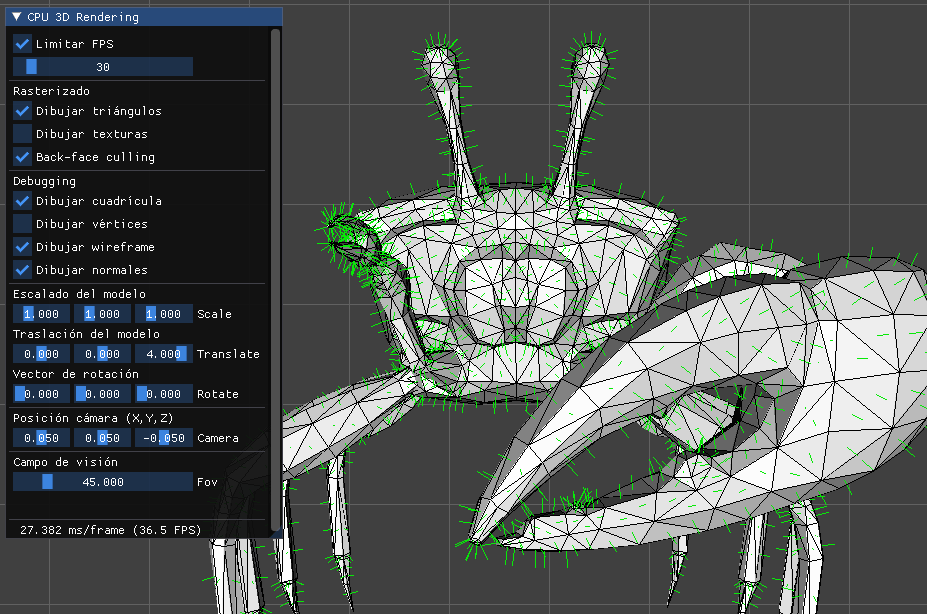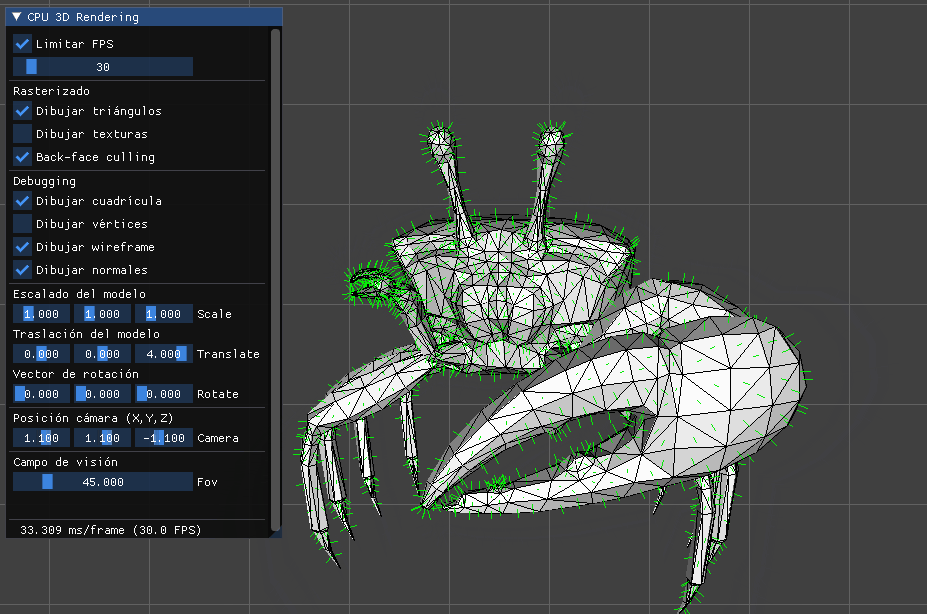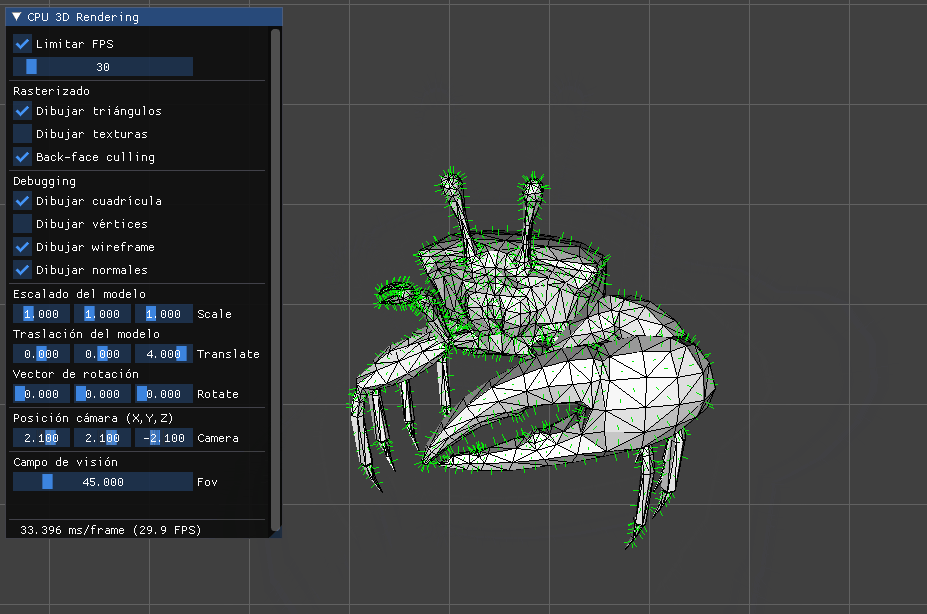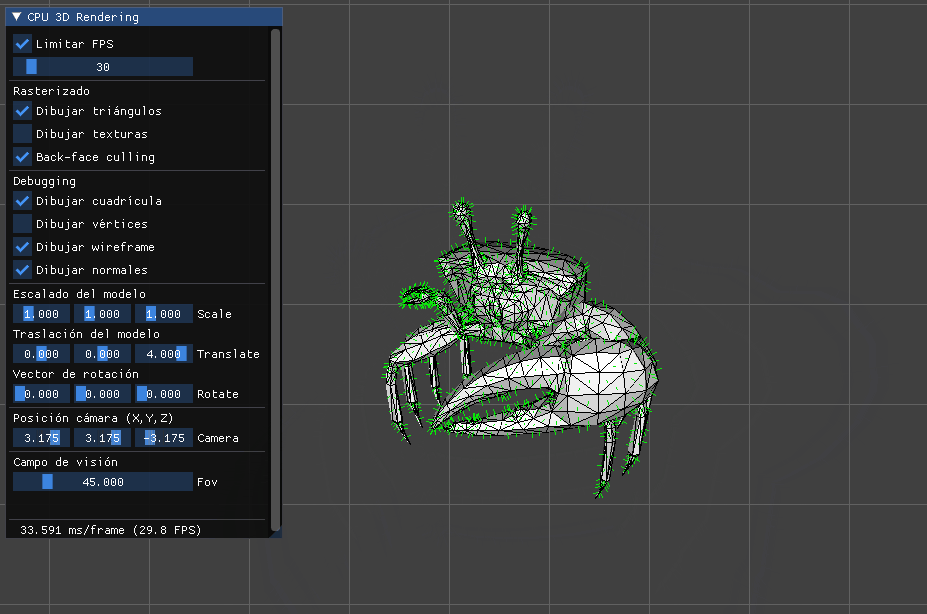
Ya podemos renderizar el escenario desde cualquier posición mirando a un punto concreto.

Variable Delta-time¶

Actualmente estamos realizando un ligero cambio en la posición de la cámara en cada fotograma para simular que ésta se aleja del modelo:

window->cameraPosition[0] += 0.025;
window->cameraPosition[1] += 0.025;
window->cameraPosition[2] -= 0.025;

El problema de estos valores es que afectan en función de los fotogramas. Cuanto mayor sea la tasa de FPS más rápido cambiará la posición de cámara porque los valores se incrementarán/decrementarán más veces.

Esto es lo que se conoce como movimiento en función de los fotogramas y si podiéramos asegurar que la tasa de FPS es completamente estable no sería un problema. Pero el caso es que eso dista mucho de la realidad, pues los FPS son tendientes a cambiar dependiendo de lo ocupado que se encuentre el procesador, incluso pueden variar por la potencia del propio procesar.

La solución es realizar el movimiento en función del tiempo, pues esa unidad es común independientemente de los FPS y para ello se almacena en una variable conocida como deltaTime la diferencia de tiempo en el que se ejecuta un fotograma y el siguiente. Usando como factor esa cantidad, que por ejemplo a 60 FPS sería 1/60 = 0.016, podemos establecer un movimiento más preciso en función del tiempo como por ejemplo "X distancia por segundo" y funcionará para cualquier tasa de FPS que tengamos.

Lo que generalmente haríamos es calcular la diferencia de SDL_GetTicks() respecto a otra variable almacenada en el anterior fotogorama. Sin embargo al haber implementado la interfaz Dear ImGui esa información nos la calcula la biblioteca automáticamente y la encontramos en ImGui::GetIO().DeltaTime.

Si el acceso nos parece demasiado largo podemos definir una variable float deltaTime en window.h:

class Window
{
public:
    /* DeltaTime*/
    float deltaTime;
};

Y establecerla con ese valor en cada fotograma:

// DeltaTime saving
deltaTime = ImGui::GetIO().DeltaTime;

Solo tendremos que utilizarla donde precisemos, por ejemplo al alejar la cámara, ahora utilizando una cantidad de distancia por segundo:

window->cameraPosition[0] += 1 * window->deltaTime;
window->cameraPosition[1] += 1 * window->deltaTime;
window->cameraPosition[2] -= 1 * window->deltaTime;

Ahora independientemente de si tenemos 5 FPS:

O 300 FPS:

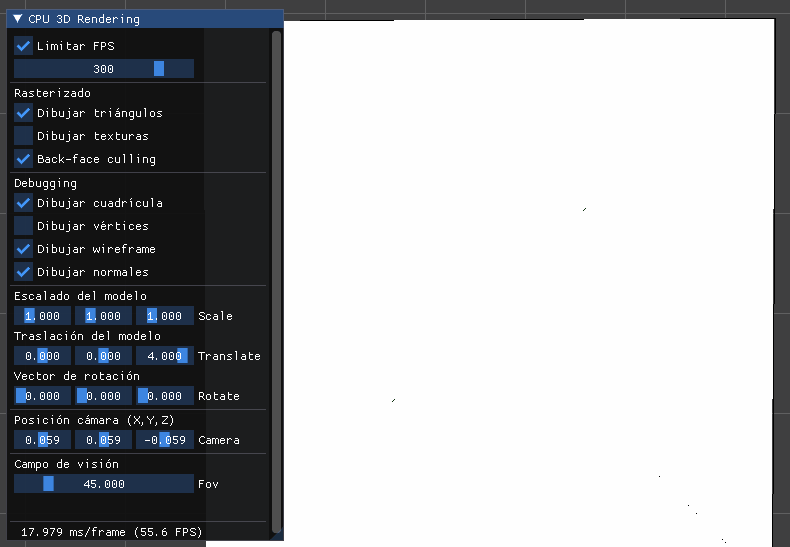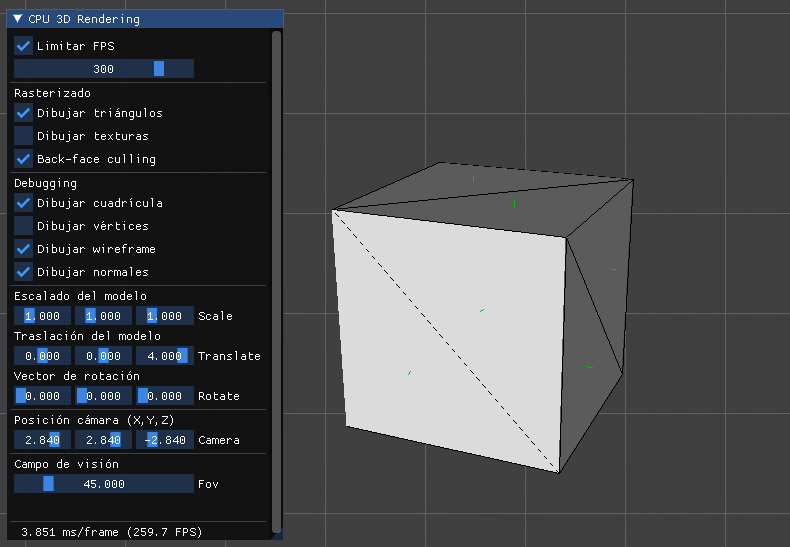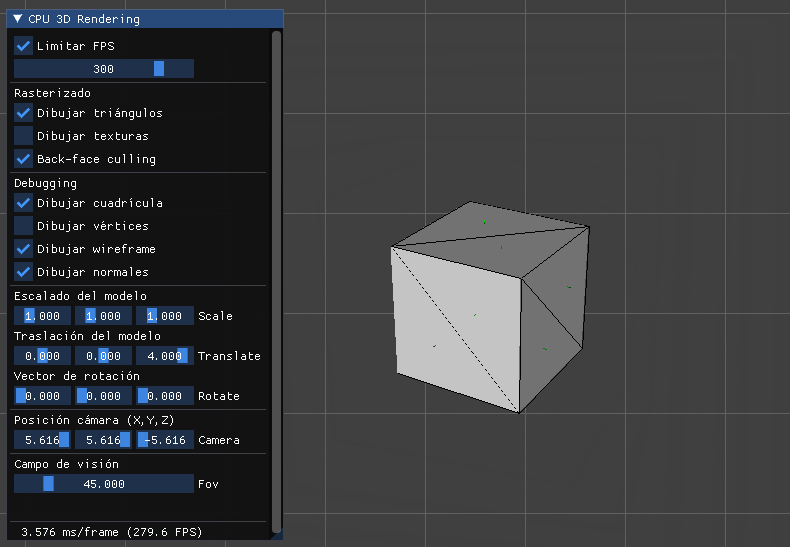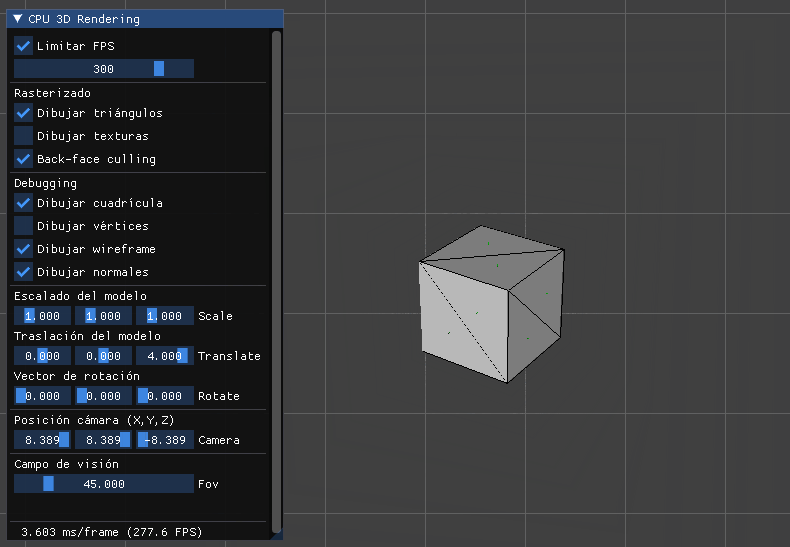
La velocidad de movimiento siempre será 1 unidad del mundo por segundo.

Cámara FPS¶

Para implementar una cámara libre tipo FPS que podamos mover a voluntad en el sistema, necesitamos considerar las diferencias respecto a una cámara lookAt:

1. Para empezar, como la cámara no tendrá un objetivo sino que apuntará hacia donde nosotros queramos, necesitaremos un vector con la dirección a parte de la posición.
2. Si podemos mover la cámara hacia adelante y atrás eso necesitamos un vector de velocidad de velocidad adelante para el eje Z, otro para moverla a la izquierda y a la derecha que podemos llamar vector de velocidad lateral para el eje X y uno para el eje Y para mover el vector de velocidad vertical hacia arriba y abajo.
3. Finalmente para rotar la cámara tanto horizontalmente como verticalmente necesitaremos diferentes ángulos conocidos como yaw y pitch, los cuales se basan en congelar un eje y realizar la rotación en el espacio a su alrededor: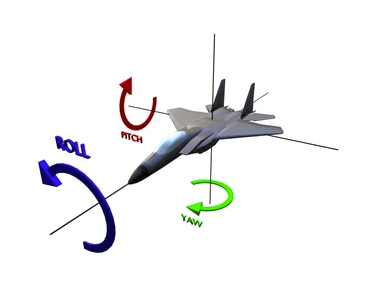

class Camera {
public:
    Vector3 position{ 0, 0, 0 };
    Vector3 direction{ 0, 0, 0 };
    Vector3 forwardVelocity{ 0, 0, 0 };
    Vector3 sideVelocity{ 0, 0, 0 };
    Vector3 verticalVelocity{ 0, 0, 0};
    float yawPitch[2]{0,0}; // y,p
};

Para ayudarme a debugear la información añadiré algunos unos campos para los ángulos en la interfaz:

ImGui::Text("Ángulos cámara (yaw,pitch,roll)");
ImGui::SliderFloat2("Angles", camera.yawPitch, -5, 5);
ImGui::Text("Posición ratón (X,Y)");
ImGui::SliderInt2("Mouse", mousePosition, 0, 0);

Además definiré un kit de variables para controlar la posición del ratón, si ha ocurrido un click y el lugar, etc:

class Window
{
public:
    /* Camera and mouse settings */
    Camera camera;
    float cameraPosition[3];
    Matrix4 viewMatrix;
    bool mouseClicked;
    int mousePosition[2];
    int mouseClickPosition[2];
};

Empezaremos por la rotación yaw y pitch, capturando los eventos SDL_MOUSEBUTTONDOWN, SDL_MOUSEBUTTONUP y SDL_MOUSEMOTION:

void Window::ProcessInput()
{
    // Update mouse positions for debugging
    SDL_GetMouseState(&mousePosition[0], &mousePosition[1]);

    while (SDL_PollEvent(&event))
    {
        ImGui_ImplSDL2_ProcessEvent(&event);
        switch (event.type)
        {
        case SDL_MOUSEBUTTONDOWN:
            mouseClicked = true;
            // Save current click position
            // SDL_GetMouseState(&mouseClickPosition[0], &mouseClickPosition[1]);
            // SDL_SetRelativeMouseMode(SDL_TRUE);
            break;
        case SDL_MOUSEBUTTONUP:
            mouseClicked = false;
            // SDL_SetRelativeMouseMode(SDL_FALSE);
            // Reset current click position
            // SDL_WarpMouseInWindow(window, mouseClickPosition[0], mouseClickPosition[1]);
            break;
        case SDL_MOUSEMOTION:
            if (mouseClicked){
                // Rotation per second in radians
                float mouseSensitivity = 0.075;
                camera.yawPitch[0] += event.motion.xrel * mouseSensitivity * deltaTime;
                camera.yawPitch[1] += event.motion.yrel * mouseSensitivity * deltaTime; 
                // Clamp the pitch between values close to -90º and 90º (-PI/2 and PI/2) to avoid flipping
                if (camera.yawPitch[1] < (-M_PI / 2 + 0.05)) camera.yawPitch[1] = -M_PI / 2 + 0.05;
                if (camera.yawPitch[1] > (M_PI / 2 - 0.05)) camera.yawPitch[1] = M_PI / 2 - 0.05;
            }
            break;
        }
    }
}

Básicamente incrementaremos los ángulos yaw y pìtch en función del movimiento del ratón en los ejes horizontal y vertical respectivamente. Cuando empiece el clic y finalice controlaremos una variable booleana mouseClicked y guardaremos la posición del click en la pantalla. Mientras el ratón está presionado podremos modificar los ángulos moviendo el ratón.

Con esto tenemos los ángulos de rotación y debemos crear la matriz de la vista para nuestra cámara FPS. Reutilizaremos el método Matrix::LookAt pero adaptando el vector objetivo target:

void Mesh::Update()
{
    //// FPS CAMERA VIEW MATRIX WITHOUT HARDCODED TARGET
    // Create an initial target vector forward the z-axis
    Vector3 target = {0, 0, 1};  
    // Calculate yaw rotation matrix and set the direction
    Matrix4 cameraYawRotationMatrix = Matrix4::RotationYMatrix(window->camera.yawPitch[0]);
    Matrix4 cameraPitchRotationMatrix = Matrix4::RotationXMatrix(window->camera.yawPitch[1]);
    window->camera.direction = target * cameraPitchRotationMatrix * cameraYawRotationMatrix;
    // Offset the camera position in the direction where the camera is pointing at
    target = window->camera.position + window->camera.direction;
    Vector3 upDirection = { 0, 1, 0 };
    // Calculate the view matrix for each frame
    window->viewMatrix = Matrix4::LookAt(window->camera.position, target, upDirection);
}

Esta parte tiene más miga pero no es tan difícil, empezaremos con un Vector3 básico para el objetivo. Es importante que tenga una profundidad Z mayor o igual a 1 porque eso implica que nuestro objetivo target estará inicialmente hacia adelante de la cámara (si el sistema utilizará la regla de la mano derecha deberíamos cambiar el número a -1).

Luego generaremos dos matrices de rotación, la del ángulo yaw a partir de nuestro método Matrix4::RotationYMatrix y la del ángulo pitch a partir del método Matrix4::RotationXMatrix y los multiplicaremos por el target para conseguir la dirección de cámara.

Una vez tengamos la cámara mirando a la dirección ya rotada en X e Y calcularemos la posición del target simplemente como el offset entre la posición de la cámara y su dirección. Con el target listo calcularemos la matriz de la vista con LookAt y ya estará, podremos rotar la vista mientras h hacemos clic en la ventana:

La segunda parte de la cámara FPS es añadir el movimiento en función de las velocidades en el eje Z y X, para lo cuál he optado por un sistema en torno a la instrucción SDL_GetKeyboardState que genera un mapa de todas las teclas presionadas justo después de procesar el while de los eventos:

// Process the WASD movement with a keyState map
{
    const uint8_t* keystate = SDL_GetKeyboardState(NULL);

    // Calculate the forwardVelocity for the z axis and increment it
    int zMovement{ keystate[SDL_SCANCODE_W] - keystate[SDL_SCANCODE_S] };
    if (zMovement != 0) 
    {
        camera.forwardVelocity = camera.direction * 5.0 * deltaTime;
        camera.position += camera.forwardVelocity * zMovement;
    }

    // Calculate the sideVelocity for the x axis and increment it
    int xMovement{ keystate[SDL_SCANCODE_A] - keystate[SDL_SCANCODE_D] };
    if (xMovement != 0) 
    {
        Vector3 vectorLeft = camera.direction.CrossProduct({ 0, 1, 0 });
        camera.sideVelocity = vectorLeft * 5.0 * deltaTime;
        camera.position += camera.sideVelocity * xMovement;
    }

    // Calculate the verticalVelocity for the y axis and increment it
    int yMovement{ keystate[SDL_SCANCODE_E] - keystate[SDL_SCANCODE_Q] };
    if (yMovement != 0)
    {
        camera.verticalVelocity = Vector3{ 0, 1, 0 } * 5.0 * deltaTime;
        camera.position += camera.verticalVelocity * yMovement;
    }

    // Set the result moving positions into the camera interface
    cameraPosition[0] = camera.position.x;
    cameraPosition[1] = camera.position.y; 
    cameraPosition[2] = camera.position.z;
}

Primero detectamos si hay movimiento en el eje Z, de manera que tengamos almacenado un factor -1, 0, 1. Si ese factor es distinto de 0 significa que hay que mover la cámara en el eje Z. Ese eje es el de la propia dirección de la cámara camera.direction, solo debemos multiplicar esa dirección por una cantidad de movimiento y tendremos la forwardVelocity para incrementar camera.position.

Luego haremos exactamente lo mismo para el eje X, pero deberemos calcular al principio un vector para el eje X de la cámara. Eso es tan fácil como hacer el producto vectorial entre la dirección a la que mira la cámara y un vector genérico hacia arriba {0,1,0}. Este vector en el eje X llamado vectorLeft marcará la dirección y lo multiplicaremos por la cantidad a movernos en ese eje para luego sumarla a la posición:

En cuanto al eje Yes el más sencillo, tan solo debemos aplicar un VectorUp genérico con la respectiva velocidad.

Luego actualizamos los valores de la interfaz de la cámara cameraPosition con la nueva posición que hemos calculado en camera.position:

Con esto he finalizado el desarrollo de la cámara FPS utilizando teclas WASD y apuntando con dirección del ratón.

Última edición: 05 de Junio de 2022