Clipping¶
Llegó la hora de implementar la última funcionalidad importante de mi sistema de renderizado, el clipping:
Empezaré enumerando sus objetivos más importantes del clipping:
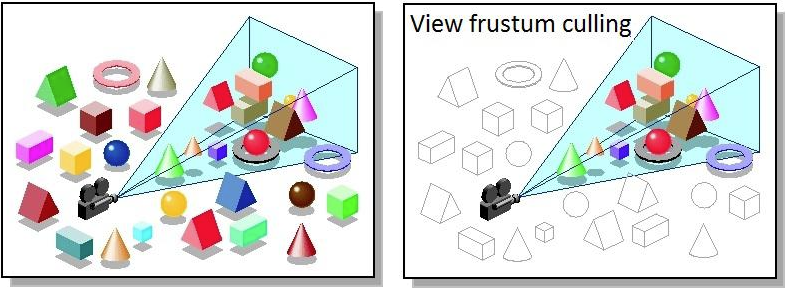
- La meta de usar clipping es eliminar los objetos o segmentos de línea que quedan fuera del volumen de la vista (aka frustum).
- El clipping 3D es un conjunto de métodos para recortar los polígonos que cortan planos.
- El pipeline define varios pasos, uno para cada plano del frustum que hay que recortar.
Es decir, no se trata solo de descartar los modelos externos al frustum sino de la capacidad de recortar los que se encuentran cortando el propio frustum y eso nos traerá bastante trabajo:

En el frustum clipping tenemos que recortar los modelos en cada uno de los seis planos por orden:
- Arriba
- Abajo
- Izquierda
- Derecha
- Cerca
- Lejos
El polígono producido por cada paso se utiliza como entrada para el siguiente, por lo que al final estamos acumulando todos estos pasos para producir el modelo recortado final.
Planos del frustum¶
Empecemos repasando qué es un plano, a fin de cuentas necesitamos 6 planos para formar un frustum.
Un plano se define como el conjunto de un punto y un vector normal:

Un punto puede tener infinitos planos dependiendo del vector normal.
Así que vamos a crear esta clase dentro de nuestra nueva cabecera clipping.h:
#ifndef CLIPPING_H
#define CLIPPING_H
#include "vector.h"
class Plane
{
public:
Vector3 point;
Vector3 normal;
};
#endif
Lo siguiente que haremos es determinar para cada plano del frustum cual es el punto y el vector normal que lo identifica. Por eso nos preguntaremos lo siguiente para cada uno:
- ¿Qué punto podemos tomar para definir un plano del frustum?
- ¿Cuáles son los componentes
X,Y,Zde su vector normal?
Plano derecho
Si suponemos que miramos desde arriba y queremos determinar el plano derecho del frustum tenemos:

El punto P podemos suponerlo como el origen o la propia cámara en (0,0,0). Mediante trigonometría encontraremos cada componente:
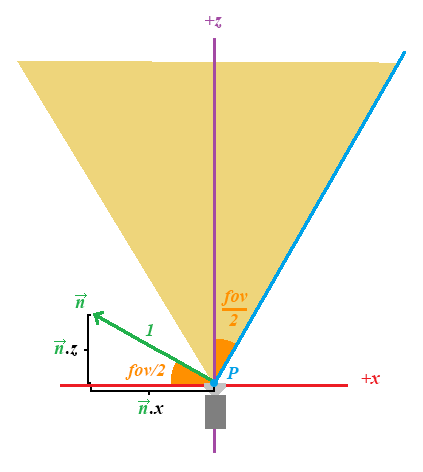
Debemos tener en cuenta que X se encuentra a la izquierda y por tanto es negativa, de ahí que el coseno sea negativo.
Plano izquierdo
Este es exactamente igual pero la X es positiva, por tanto el ángulo del coseno será positivo:
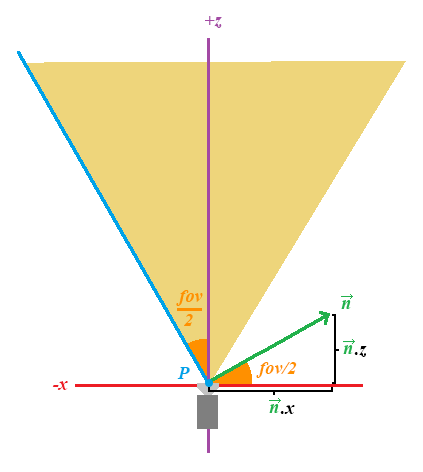
Plano superior
Ahora vamos a cambiar de perspectiva, vamos a ver el frustum desde el lado. Así podemos conseguir Y y Z:

Dado que la Y es negativa, el coseno del ángulo será negativo:
Plano inferior
Cambiando al plano de abajo, el único cambio es que la Y es ahora positiva, por tanto el coseno será positivo:
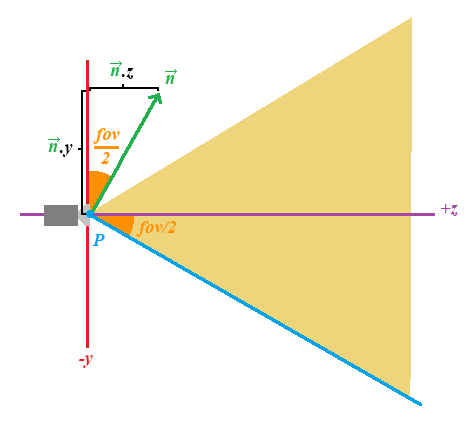
Plano cercano
Para poner en perspectiva la profundidad la vamos a visualizar desde el lado, suponiendo que tenemos un plano cercano cortando el frustum:
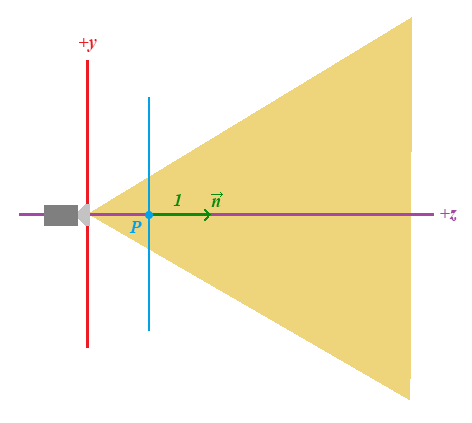
En esta ocasión el punto P ya no será (0,0,0) sino que la profundidad Z vendrá marcada por el valor znear y la longitud normalizada es 1 hacia adelante, por tanto positiva:
Plano alejado
Prácticamente con la misma lógica determinamos el plano más lejos en profundidad:
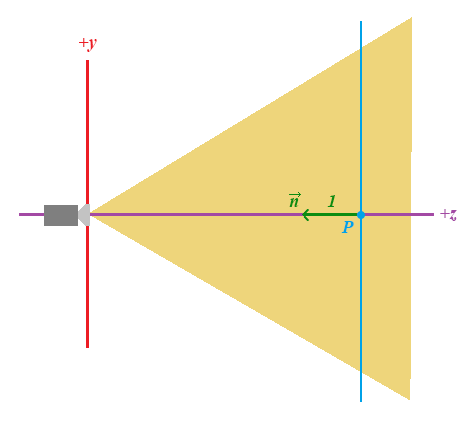
la diferencia es que ahora la profundidad del punto P la determina nuestro valor zfar y el vector normal apunta hacia adentro, por lo que será negativo:
Con la información de los planos podemos codificar un método para inicializar una nueva clase frustum en función del valor fov, znear y zfar:
#include <math.h>
class Frustum
{
public:
Plane leftPlane;
Plane rightPlane;
Plane topPlane;
Plane bottomPlane;
Plane nearPlane;
Plane farPlane;
Frustum(float fov, float zNear, float zFar)
{
float cosHalfFov = cos(fov/2);
float sinHalfFov = sin(fov/2);
leftPlane.point = Vector3{0,0,0};
leftPlane.normal = Vector3{cosHalfFov,0,sinHalfFov};
rightPlane.point = Vector3{0,0,0};
rightPlane.normal = Vector3{-cosHalfFov,0,sinHalfFov};
topPlane.point = Vector3{0,0,0};
topPlane.normal = Vector3{0,-cosHalfFov,sinHalfFov};
bottomPlane.point = Vector3{0,0,0};
bottomPlane.normal = Vector3{0,cosHalfFov,sinHalfFov};
nearPlane.point = Vector3{0,0,zNear};
nearPlane.normal = Vector3{0,0,1};
farPlane.point = Vector3{0,0,zFar};
farPlane.normal = Vector3{0,0,-1};
}
};
Inicializaré un viewFrustum justo después de crear la matriz de proyección:
#include "clipping.h"
class Window
{
public:
/* Projection and frustum settings */
float fovFactorInGrades = 60;
float fovFactor = M_PI / (180 / 60.0f); // in radians
float aspectRatio;
float zNear = 0.1, zFar = 20.0;
Matrix4 projectionMatrix;
Frustum viewFrustum; // <-----------
Window() : windowWidth(1280), windowHeight(720), rendererWidth(965), rendererHeight(655)
{
aspectRatio = rendererHeight / static_cast<float>(rendererWidth);
projectionMatrix = Matrix4::PerspectiveMatrix(fovFactor, aspectRatio, zNear, zFar);
viewFrustum = Frustum(fovFactor, zNear, zFar); // <-----------
};
};
Punto respecto a un plano¶
Lo siguiente que debemos tener en cuenta es cómo saber si un punto, por ejemplo punto Q, se encuentra dentro o fuera de un plano, teniendo en cuenta que el vector normal apunta hacia dentro del plano. Esto nos permitirá identificar los vértices fuera del frustum, descartarlos o recortarlo.
El cálculo que nos permitirá determinar esta cuestión es el producto escalar del vector Q - P por la normal del plano y tenemos tres posibilidades:
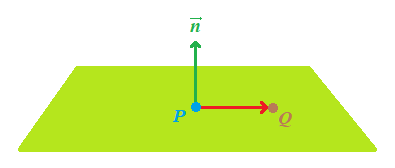
Dentro del plano
El punto Q estará dentro del plano si el resultado del producto escalar es mayor que 0:
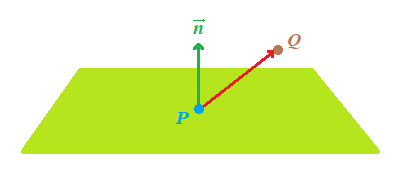
Fuera del plano
El punto Q estará fuera del plano si el resultado del producto escalar es menor que 0:
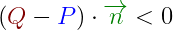
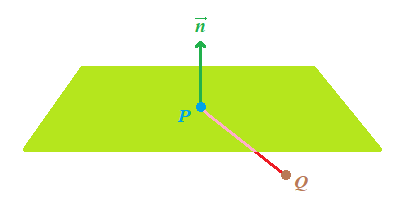
Alineado sobre el plano
El punto Q estará alineado sobre el plano si el resultado del producto escalar es igual 0:
Punto de intersección¶
Sabiendo cómo determinar si un punto Q se encuentra dentro o fuera de un plano ya podemos descartar los vértices fuera del frustum.
Si todos los vértices de una malla están fuera del frustum simplemente la ignoramos y no la dibujamos, pero... ¿Y si la malla tiene algunos vértices dentro y otros fuera del plano?
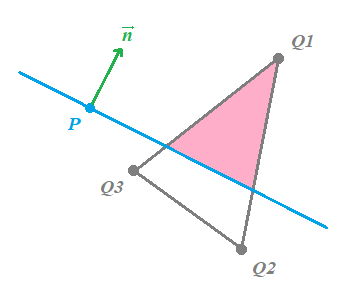
En ese caso lo siguiente que debemos encontrar son los puntos de intersección entre el plano y el polígono:
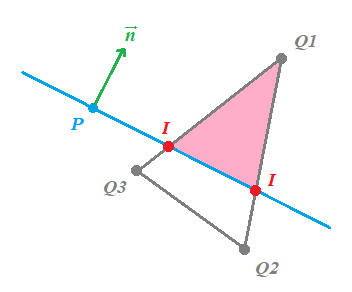
Bueno, en realidad lo que queremos encontrar es el punto de intersección entre un segmento de una línea y una plano:
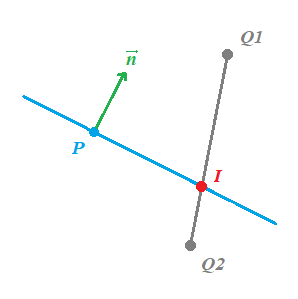
Podemos interpolar cualquier punto de este segmento mediante la ecuación de interpolación lineal:
Donde t es un factor entre 0 y 1 cuyo valor nos dará cualquier punto entre el segmento Q1 y Q2, siendo I = Q1 si t = 0 o I = Q2 si t = 1.
Extrapolando, para encontrar el punto de intersección I necesitamos encontrar el factor de interpolación t. Este procedimiento no es fácil, un desglose de la técnica se puede encontrar en este paper.
Después de aplicar toda la magia el factor t se puede encontrar aplicando la fórmula:
Donde el factor t es igual al producto escalar del punto Q1 dividido entre la resta del producto escalar de Q1 menos el producto escalar de Q2.
Con esto la fórmula para encontrar el punto de intersección queda completada:
Algoritmo de clipping¶
En este punto ya podemos hacernos una idea del procedimiento de clipping:
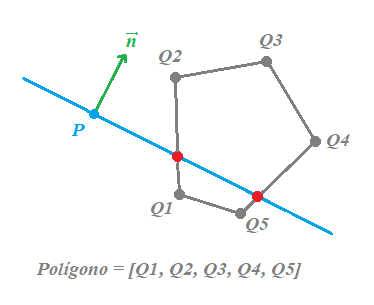
Al final la idea se basa en subtituir los vértices fuera de los planos por los puntos de intersecciónen, dando lugar a un nuevo polígono:

Esto sería el recorte para un plano, tendremos que repetir el proceso para cada plano del frustum (arriba, abajo, izquierda, derecha, cercano y alejado), utilizando como entrada el polígono resultante de cada recorte anterior:
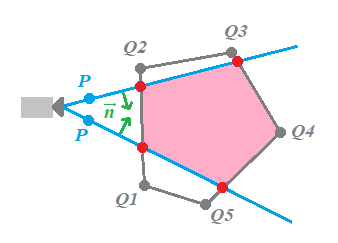
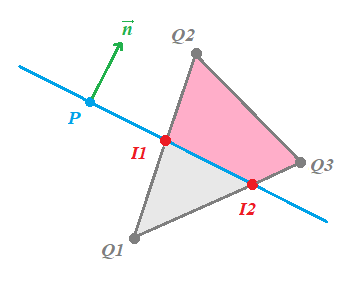
La función que implementará todo este procedimiento para los seis planos tomará un polígono (una nueva clase Poligon en clipping.h) creado inicialmente con un triángulo y que podrá tener un número indeterminado de vértices, debido a que después del corte, pueden generarse nuevos vértices como en este ejemplo que al cortar un triángulo obtenemos un polígono de cuatro costados:
#include <deque>
#include "vector.h"
#include "triangle.h"
class Polygon
{
public:
std::deque<Vector3> vertices;
Polygon(Triangle triangle)
{
// Save the starting triangle vertices
vertices.push_back(triangle.vertices[0]);
vertices.push_back(triangle.vertices[1]);
vertices.push_back(triangle.vertices[2]);
}
};
En esta clase tendremos al fin el método Clip para aplicar todo el algoritmo plano por plano con otro método ClipAgainstPlane:
class Polygon
{
public:
void Clip(Frustum viewFrustum)
{
ClipAgainstPlane(viewFrustum.leftPlane);
ClipAgainstPlane(viewFrustum.rightPlane);
ClipAgainstPlane(viewFrustum.topPlane);
ClipAgainstPlane(viewFrustum.bottomPlane);
ClipAgainstPlane(viewFrustum.nearPlane);
ClipAgainstPlane(viewFrustum.farPlane);
}
private:
void ClipAgainstPlane(Plane plane)
{
// Lógica del recorte
}
};
El clipping lo ejecutaremos antes del culling y proyectar los puntos, justo después de las transformaciones 3D.
Crearemos nuestro polígono, realizaremos los recortes del clipping y como resultado posiblemente obtendremos un polígono con muchos más vértices que posteriormente deberemos transformar de nuevo a triángulos:
#include "clipping.h"
void Mesh::Update()
{
// Loop all triangle faces of the mesh
for (size_t i = 0; i < triangles.size(); i++)
{
/*** CLIPPING: BEFORE THE PROJECTION */
// Create the initial polygon with the triangle face vertices
Polygon polygon(triangles[i]);
// Then do the clipping
polygon.Clip(window->viewFrustum);
}
Ahora viene el desarrollo de la función ClipAgainstPlane que a partir del corte con un plano determinará la nueva lista de vértices del polígono:
void ClipAgainstPlane(Plane plane)
{
// Creamos una cola para almacenar los vértices dentro del plano
std::deque<Vector3> insideVertices;
// Recorremos todos los vértices
for (size_t i = 0; i < vertices.size(); i++)
{
// Recuperamos el vértice actual y el anterior
Vector3 currentVertex = vertices[i];
// Si recién empezamos (i==0) el anterior será el último
Vector3 previousVertex = (i > 0) ? vertices[i - 1] : vertices[vertices.size() - 1];
// Calculamos los productos escalares de ambos (dotQ1 = n·(Q1-P))
float currentDot = (currentVertex - plane.point).DotProduct(plane.normal);
float previousDot = (previousVertex - plane.point).DotProduct(plane.normal);
// Si el vértice está fuera del plano calculamos el punto de intersección
// Podemos saberlo si uno es positivo y el otro es negativo, signigicando esto
// que un punto a pasado a estar de dentro a fuera o viceversa, de fuera a dentro
if (currentDot * previousDot < 0)
{
// Calculamos el factor de interpolación, t = dotQ1/(dotQ1-dotQ2)
float tFactor = previousDot / (previousDot - currentDot);
// Calculamos el punto de intersección, I = Q1 + t(Q2-Q1)
Vector3 intersectionPoint = currentVertex; // I = Qc
intersectionPoint -= previousVertex; // I = (Qc-Qp)
intersectionPoint *= tFactor; // I = t(Qc-Qp)
intersectionPoint += previousVertex; // I = Qp+t(Qc-Qp)
// Insertamos el nuevo punto de intersección a la lista de vértices internos
insideVertices.push_back(intersectionPoint);
}
// Si el vértice se encuentra dentro del plano lo añadimos a la cola
if (currentDot > 0) insideVertices.push_back(currentVertex);
}
// Copiamos los vértices dentro del plano a los vértices actuales
vertices.clear();
vertices = insideVertices;
}
En este punto si estamos renderizando un cubo, si miramos cuál es el índice del primer triángulo definido en el cube.obj que en mi caso es el 5, podemos hacer un bypass para renderizar solo el primer triángulo:
void Mesh::Update()
{
// Loop all triangle faces of the mesh
for (size_t i = 0; i < triangles.size(); i++)
{
// bypass para debugear solo el primer triángulo
if (i != 5) continue;
Si imprimimos el número de vértices del polígono después de recortarlo:
polygon.Clip(window->viewFrustum);
std::cout << "Polygon vertices: " << polygon.vertices.size() << std::endl;
Deberíamos ver como cambia el contador dependiendo de cómo lo cortemos, por ejemplo recortando por arriba obtendremos 3 vértices:
Recortando por la izquierda 4 vértices:
Por abajo a la izquierda 5 vértices:
En conclusión parece que funciona.
De polígonos a triángulos¶
El siguiente objetivo es transformar el polígono formado por una cantidad indeterminado de vértices de nuevo a triángulos para renderizararlos.
Para conseguirlo podemos unir el primer vértice del polígono con el segundo y el tercero, de nuevo el primero con el tercero y el cuarto, el primero con el cuarto y el quinto... Así sucesivamente hasta el penúltimo vértice (-2 respecto a la longitud de la cola):
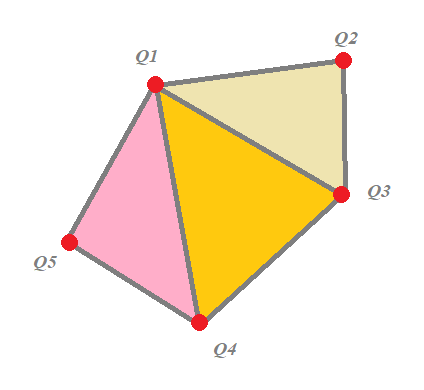
La implementación es fácil, en un método GenerateClippedTriangles iremos metiendo los triángulos recortados en una cola que pasaremos por referencia:
class Polygon
{
public:
void GenerateClippedTriangles(std::deque<Triangle>& clippedTriangles)
{
// Ensure a minimum of 3 vertices to create a new triangle
if (vertices.size() > 2)
{
for (size_t i = 0; i < vertices.size() - 2; i++)
{
int index0 = 0;
int index1 = i + 1;
int index2 = i + 2;
Triangle triangle = Triangle(0xFFFFFFFF);
triangle.vertices[0] = vertices[index0];
triangle.vertices[1] = vertices[index1];
triangle.vertices[2] = vertices[index2];
clippedTriangles.push_back(triangle);
}
}
}
};
Esta cola la crearé en el mesh y se llamará clippedTriangles:
class Mesh
{
public:
std::deque<Triangle> clippedTriangles;
};
La reiniciaré siempre al principio del Update para no acumular los triángulos recortados entre fotogramas:
void Mesh::Update()
{
// Clear all the clippedTriangles for the current frame
clippedTriangles.clear();
Luego añadiré todos los nuevos triángulos generados durante el clipping:
// Create the initial polygon with the triangle face vertices
Polygon polygon(triangles[i]);
// Then do the clipping
polygon.Clip(window->viewFrustum);
// Add the new triangles to the clippedTriangles dequeue
polygon.GenerateClippedTriangles(clippedTriangles);
Finalizaré el primer bucle for e iniciaré otro para calcular las normales, hacer el culling y proyectar los triángulos recortados, ahora con clippedTriangles en lugar de triangles:
// PROJECTING: Loop all clippedTriangles and project them
for (size_t i = 0; i < clippedTriangles.size(); i++)
Y lo mismo para los triángulos en el Render, ahora tomándolos de clippedTriangles:
// RENDERING: Loop all projected clippedTriangles and render them
for (size_t i = 0; i < clippedTriangles.size(); i++)
En este punto, aunque con algún bug en el frustum, se deberían recortar los triángulos, formarse nuevos polígonos y transformarse de nuevo en triángulos:

Ajustando el ángulo FOV¶
Por alguna razón ahora mismo se está considerando el espacio de clipping algo así:
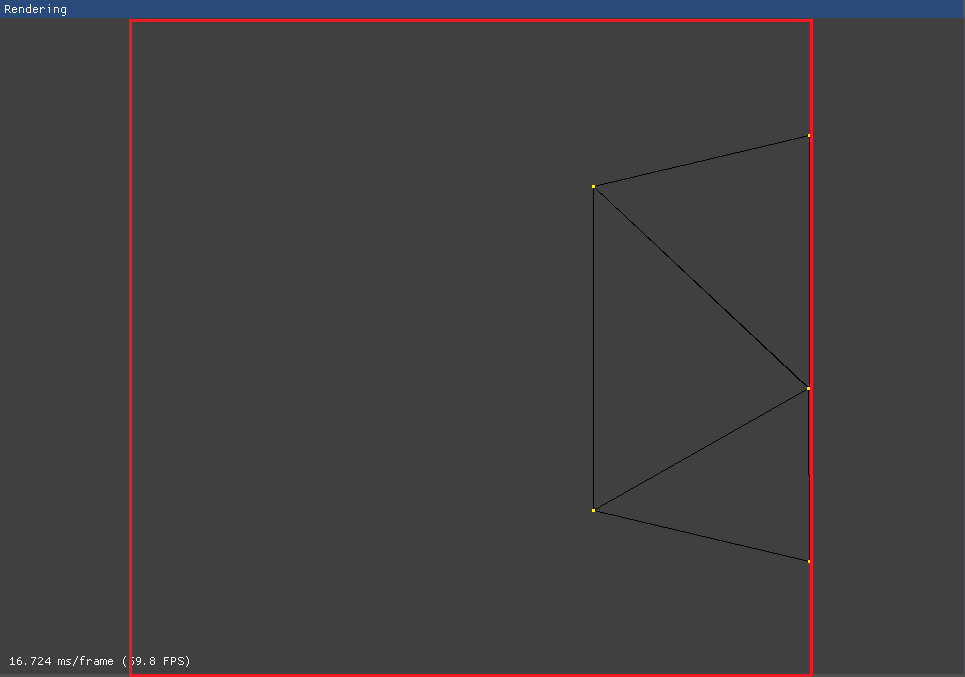
Solo con observar podemos suponer que se está tomando el mismo ancho que alto para el frustum y es que al crearlo utilizamos un fovFactor basado en el aspectRatio de la altura respecto a la anchura:
aspectRatio = rendererHeight / static_cast<float>(rendererWidth);
viewFrustum = Frustum(fovFactor, zNear, zFar);
En otras palabras es un fovFactor vertical y por ello el ancho del frustum es exactamente igual a su altura.
Para solucionar este problema empezaremos diferenciando entre un fovFactorX y un fovFactorY, lo cuál nos llevará también a tener dos relaciones de aspecto aspectRatioX y aspectRatioY:
/* Projection and frustum settings */
float fovInGrades = 60;
float fovYInGrades = fovInGrades;
float fovXInGrades = fovInGrades;
float fovFactorY = M_PI / (180 / fovInGrades); // radians
float fovFactorX = ????;
float aspectRatioX;
float aspectRatioY;
float zNear = 1.0, zFar = 20.0;
En este artículo de la Wikipedia se explica cómo determinar el fovFactorXque al final resulta en la fórmula:
#include <math.h>
float fovFactorX = 2 * atan(tan(fovFactorY/2) * aspectRatioX);
Ahora para iniciar la matriz de proyección utilizaremos el factor y relación de aspecto vertical y para el frustum pasaremos tanto el el factor horizontal como vertical para rectificarlo en ancho:
Window() : windowWidth(1280), windowHeight(720), rendererWidth(965), rendererHeight(655)
{
projectionMatrix = Matrix4::PerspectiveMatrix(fovFactorY, aspectRatioY, zNear, zFar);
viewFrustum = Frustum(fovFactorX, fovFactorY, zNear, zFar);
};
Deberemos adaptar el código del frustum para aplicar el cálculo rectificado del plano izquierdo y derecho con el nuevo fovFactorX:
Frustum(float fovFactorX, float fovFactorY, float zNear, float zFar)
{
float cosHalfFovX = cos(fovFactorX / 2);
float sinHalfFovX = sin(fovFactorX / 2);
float cosHalfFovY = cos(fovFactorY / 2);
float sinHalfFovY = sin(fovFactorY / 2);
leftPlane.point = Vector3{ 0, 0, 0 };
leftPlane.normal = Vector3{ cosHalfFovX, 0, sinHalfFovX };
rightPlane.point = Vector3{ 0, 0, 0 };
rightPlane.normal = Vector3{ -cosHalfFovX, 0, sinHalfFovX };
topPlane.point = Vector3{ 0, 0, 0 };
topPlane.normal = Vector3{ 0, -cosHalfFovY, sinHalfFovY };
bottomPlane.point = Vector3{ 0, 0, 0 };
bottomPlane.normal = Vector3{ 0, cosHalfFovY, sinHalfFovY };
nearPlane.point = Vector3{ 0, 0, zNear };
nearPlane.normal = Vector3{ 0, 0, 1 };
farPlane.point = Vector3{ 0, 0, zFar };
farPlane.normal = Vector3{ 0, 0, -1 };
}
Con esto ya estaría, pero como estamos permitiendo adaptar el fovFactor desde la interfaz tendremos que rectificar esa parte y generar de nuevo tanto la matriz de proyección como el frustum con el nuevo ángulo (convirtiéndolo a radianos) :
ImGui::SliderFloat("Fov", &this->fovInGrades, 30, 120);
// Update the Projection Matrix and thr Frustum
fovFactorY = M_PI / (180 / fovInGrades); // in radians
fovFactorX = 2 * atan(tan(fovFactorY / 2) * aspectRatioX); // in radians
projectionMatrix = Matrix4::PerspectiveMatrix(fovFactorY, aspectRatioY, zNear, zFar);
viewFrustum = Frustum(fovFactorX, fovFactorY, zNear, zFar);
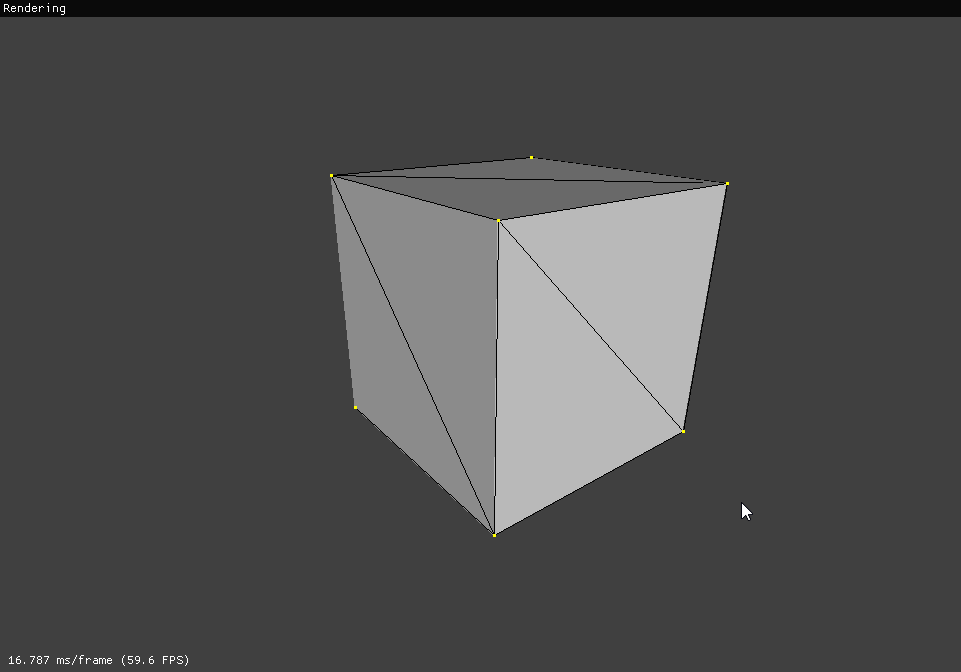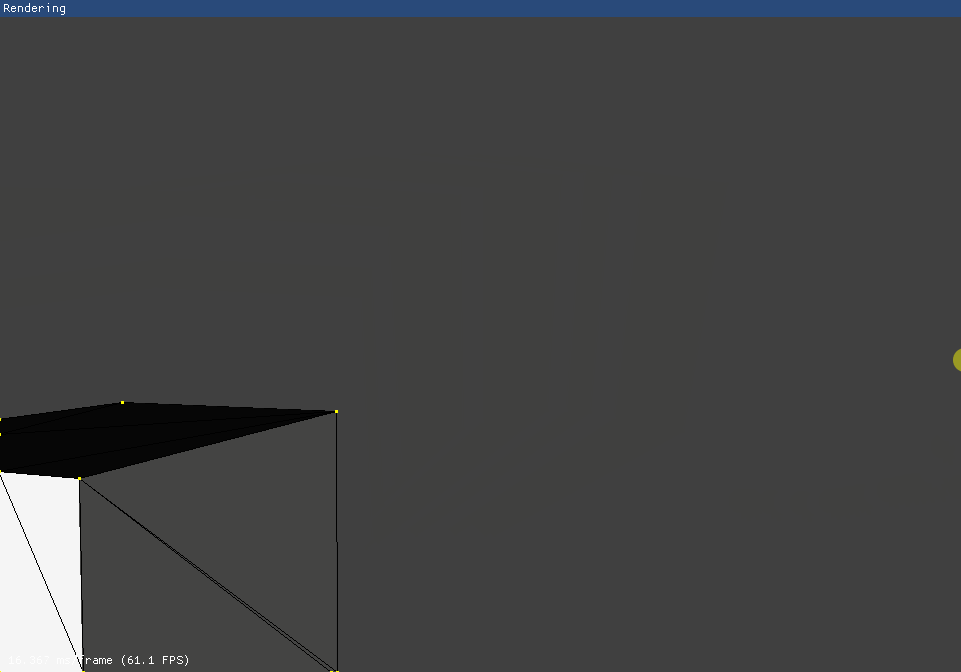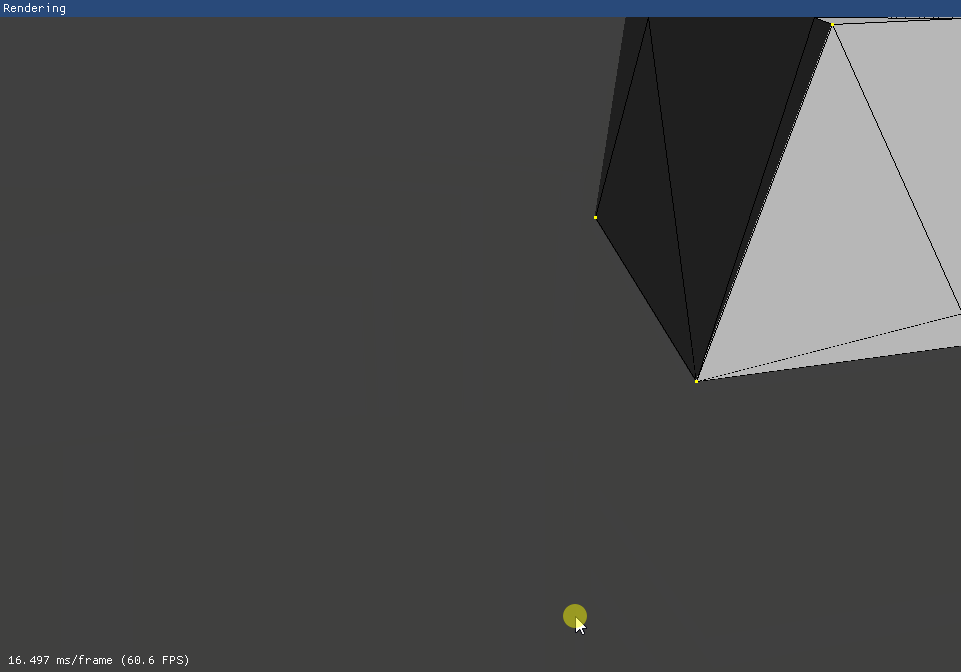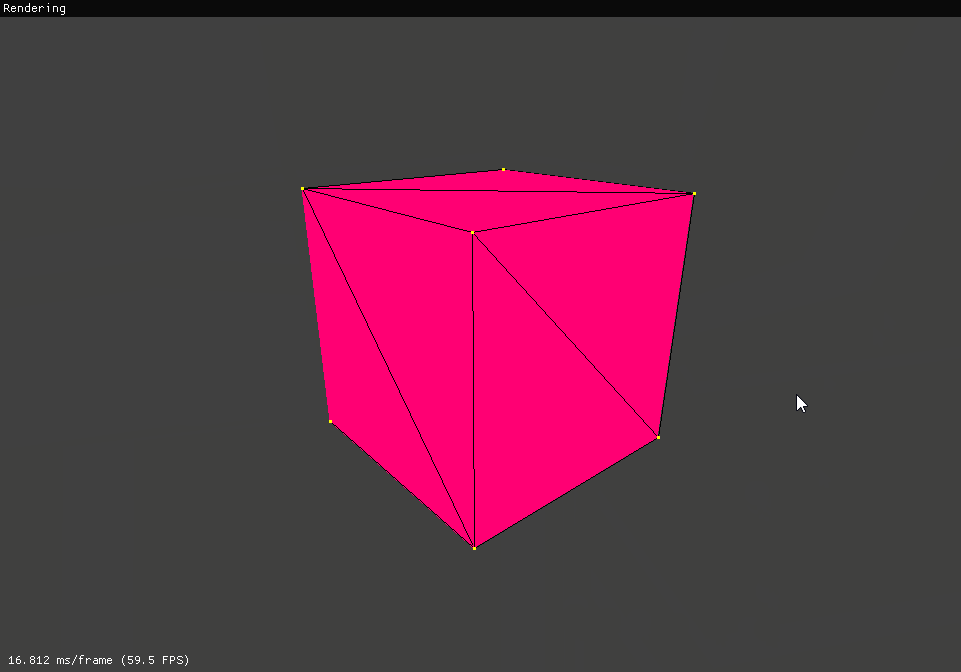
Con esto tendremos perfectamente configurado el frustum de la cámara:

El coloreado de triángulos también debería funcionar, pero el texturizado tendremos que rectificarlo:
Clipping en las texturas¶
La información de la textura de cada cara está contenida en el triángulo que enviamos al polígono y almacenamos en sourceTriangle, por lo que podemos empezar almacenándolas en una cola durante la creación del mismo:
class Polygon
{
public:
std::deque<Texture2> textureUVCoords;
Polygon(Triangle triangle)
{
// Save the starting triangle UV Coords
textureUVCoords.push_back(triangle.textureUVCoords[0]);
textureUVCoords.push_back(triangle.textureUVCoords[1]);
textureUVCoords.push_back(triangle.textureUVCoords[2]);
}
};
Lo que haremos es, durante el clipping de cada plano, recuperar las coordenadas UV para la textura del triángulo actual y el anterior de la misma forma que hicimos con los vértices:
// Recuperamos las coordenadas UV actuales y anteriores
Texture2 curTexUVCoords = textureUVCoords[i];
// Si recién empezamos (i==0) el anterior será el último
Texture2 prevTexUVCoords = (i > 0) ? textureUVCoords[i - 1] : textureUVCoords[textureUVCoords.size() - 1];
Empezamos a recorrer todos los vértices y empecemos por la parte fácil, ¿qué hacer con las coordenadas cuando el vértice se encuentra dentro del plano? Pues evidentemente añadirlas a una cola insideTextureUVCoords que crearemos al principio y al final de todos las añadiremos de nuevo a la cola:
void ClipAgainstPlane(Plane plane)
{
// Creamos una cola para almacenar las coordenadas UV de las tetxturas dentro del plano
std::deque<Texture2> insideTextureUVCoords;
//...
// Si el vértice se encuentra dentro del plano
if (currentDot > 0)
{
// Lo añadimos a la cola
insideVertices.push_back(currentVertex);
// Y también añadimos la textura
insideTextureUVCoords.push_back(curTexUVCoords);
}
// Copiamos las coordenadas de las texturas UV dentro del plano a las actuales
textureUVCoords.clear();
textureUVCoords = insideTextureUVCoords;
}
Nos falta implementar el otro caso, cuando el vértice se encuentre fuera del plano. Para ello tendremos que interpolar la posición de las coordenadas reutiliando el mismo factor t de los vértices:
Podemos utilizar nuestra propia función FloatLerp que recibe dos valores y devuelve la interpolación en función de un tercer factor. Luego la insertamos en la cola:
if (currentDot * previousDot < 0)
{
// Find the interpolation factor t
float t = previousDot / (previousDot - currentDot);
// Use a lerp formula to get the interpolated U & V texture coords
Texture2 interpolatedTexUVCoord;
interpolatedTexUVCoord.u = FloatLerp(prevTexUVCoords.u, curTexUVCoords.u, tFactor);
interpolatedTexUVCoord.v = FloatLerp(prevTexUVCoords.v, curTexUVCoords.v, tFactor);
// Insertamos las coordenadas de la nueva textura interpolada
insideTextureUVCoords.push_back(interpolatedTexUVCoord);
}
La fórmula la podemos definir de forma estática en la propia clase:
static float FloatLerp(float a, float b, float f)
{
return a + f * (b - a);
}
Ya que estamos podemos utilizar nuestra nueva función podemos substituir todo el cálculo del punto de intersección de forma mucho más sencilla. El bloque completo quedará:
// Si el vértice está fuera del plano...
if (currentDot * previousDot < 0)
{
// Calculamos el factor de interpolación, t = dotQ1/(dotQ1-dotQ2)
float tFactor = previousDot / (previousDot - currentDot);
// Calculamos el punto de intersección interpolado, I = Q1 + t(Q2-Q1)
Vector3 intersectionPoint;
intersectionPoint.x = FloatLerp(previousVertex.x, currentVertex.x, tFactor);
intersectionPoint.y = FloatLerp(previousVertex.y, currentVertex.y, tFactor);
intersectionPoint.z = FloatLerp(previousVertex.z, currentVertex.z, tFactor);
// Insertamos el nuevo punto de intersección a la lista de vértices internos
insideVertices.push_back(intersectionPoint);
// Calculamos las coordenadas de las texturas UV interpoladas
Texture2 interpolatedTexUVCoord;
interpolatedTexUVCoord.u = FloatLerp(prevTexUVCoords.u, curTexUVCoords.u, tFactor);
interpolatedTexUVCoord.v = FloatLerp(prevTexUVCoords.v, curTexUVCoords.v, tFactor);
// Insertamos las nueva coordenadas de la textura interpolada
insideTextureUVCoords.push_back(interpolatedTexUVCoord);
}
Finalmente estableceremos las nuevas texturas en los triángulos al momento de generar los triángulos del polígono:
void GenerateClippedTriangles(std::deque<Triangle>& clippedTriangles)
{
// Ensure a minimum of 3 vertices to create a new triangle
if (vertices.size() >= 3)
{
for (size_t i = 0; i < vertices.size() - 2; i++)
{
int index0 = 0;
int index1 = i + 1;
int index2 = i + 2;
Triangle clippedTriangle = Triangle(0xFFFFFFFF);
// Set the vertices
clippedTriangle.vertices[0] = vertices[index0];
clippedTriangle.vertices[1] = vertices[index1];
clippedTriangle.vertices[2] = vertices[index2];
// Set the texture UV coords
clippedTriangle.textureUVCoords[0] = textureUVCoords[index0];
clippedTriangle.textureUVCoords[1] = textureUVCoords[index1];
clippedTriangle.textureUVCoords[2] = textureUVCoords[index2];
clippedTriangles.push_back(clippedTriangle);
}
}
}
Con esto el clipping para las texturas debería funcionar:

Ha sido un largo camino empezando por la creación del frustum con sus diferentes planos, el recorte de los vértices de los triángulos dando lugar a polígonos de lados indeterminados, la interpolación de los nuevos vértices y texturas para finalmente regenerar nuevos triángulos, pero ha valido la pena.
Ahora el sistema de renderizado está mucho más optimizado, el clipping nos ahorra renderizar elementos descartados y además evita que se bloquee por los vértices por detrás de la cámara:

Frustum clipping y space clipping¶
Al final el proceso de realizar el clipping es bastante costoso para nuestra CPU. Debemos tener en cuenta que se ejecuta todo el procedimiento de recortar los polígonos, regenerar los triángulos y todas sus interpolaciones en cada fotograma. Con una malla formada por pocos triángulos no se notará, como un cubo de 8 vértices el rendimiento es exagerado y fácilmente llego a los 300 FPS:

Pero con otros modelos con un número de triángulos mucho mayor, como este dron con 7750 vértices la tasa de fotogramas se reduce drásticamente hasta apenas alcanzar los 25 FPS de media:

Repasando el rendering pipeline de mi sistema:
- Model space: El modelo empieza en su propio espacio codificado tal como se ha creado en un programa de modelado.
- World space: Aplicamos la transformación de mundo para ubicarlo en nuestro espacio 3D.
- View space: Aplicamos la transformación de la vista para visualizarlo desde nuestra cámara.
- Back-face culling: Mediante el cálculo de las normales determinamos qué triángulos no son visibles por la cámara y les hacemos un bypass.
- Frustum clipping: Realizamos el descarte y recorte de los triángulos para cada plano del frustum regenerando los triángulos mediante la interpolación de los vértices y coordenadas.
- Projection: Aplicamos la matriz de proyección para transformar el espacio 3D a 2D.
- Perspective divide: Realizamos los cálculos de la brecha de perspectiva para generar el efecto de profundidad.
- Image space: Conseguimos el espacio de valores normalizados (NDC).
- Screen space: En este punto tendremos los valores preparados para dibujarlos en la pantalla pero todavía faltará aplicar diferentes rectificaciones para ubicar los elementos en el lugar adecuado.
La realidad es que la mayoría de renders y APIs para GPUs (DirectX, OpenGL, Vulkan...) no implementan el clipping a nivel del frustum antes de la proyección, sino que lo implementan después de la proyección en su propio clipping space y antes de aplicar la brecha de perspectiva:
- Model space
- World space
- View space
- Projection
- Clipping space <---------
- Perspective divide
- Image space (NDC)
- Screen space
En este espacio se realiza tanto el culling como el clipping (homogeneuos clipping) respecto al frustum, lo que les otorga algunas ventajas.
Durante el frustum culling:
- La brecha de perspectiva es la encargada de dividir cada
X,Y,ZentreW. - Como el clipping space ocurre antes de la brecha de perspectiva es fácil determinar si los componentes
X,Y,Zde cada vértice se encuentran dentro del frustum, entre(-1 * w)y(+1 * w). - Para realizar el frustum culling la mayoría de renders simplemente comparan cada componente con
W.
Durante el frustum clipping:
- Las coordenadas de las texturas pueden ser interpoladas linealmente porque todavía no se ha realizado la brecha de perspectiva.
- La división entre cero se evita porque se realiza el culling y el clipping teniendo en cuenta siempre la variable
znear.
Por mi parte como este proyecto tiene la finalidad de aprender, creo que implementar el clipping antes de la proyección es más entendible. Al separar la lógica del espacio 3D y del plano 2D he podido desarrollar el procedimiento visualizando cada paso.
Para profundizar sobre los algoritmos de culling recomiendo el artículo de la Wikipedia sobre la determinación de las caras ocultas. Los llamados algoritmos HSR (Hidden Surface Determination), OC (Oclusion culling) o el VSD (Visible Surface Determination) abarcan todo tipo de técnicas desde el Z-Buffer, el algoritmo del pintor o el Ray tracing, vale la pena echar un vistazo.
Última edición: 05 de Junio de 2022
