Colisiones entre Líneas¶

Las líneas en los videojuegos suelen representar los lados de una estructura, el suelo o también el camino de un objeto en movimiento. Por tanto si queremos saber si un objeto choca contra el suelo para que no lo traspase (o contra otro objeto) tendremos que comprobar si la línea que sigue su camino cruza la línea de suelo (o el camino de otro objeto). En otras palabras, tendremos que programar una condición basada en la intersección de dos líneas.

Por ahora ya sabemos como encontrar las ecuaciones de estas líneas, así que podemos ponerlas juntas y formar un sistema de ecuaciones lineales para resolverlo matemáticamente.

Sistemas de ecuaciones lineales¶

Al resolver un sistema de dos ecuaciones lineales, lo que en realidad estás buscando es la intersección de dos líneas, es decir, el conjunto de soluciones con todos los puntos que satisfacen ambas ecuaciones. El teorema nos indica tres soluciones para dos líneas en el mismo plano.

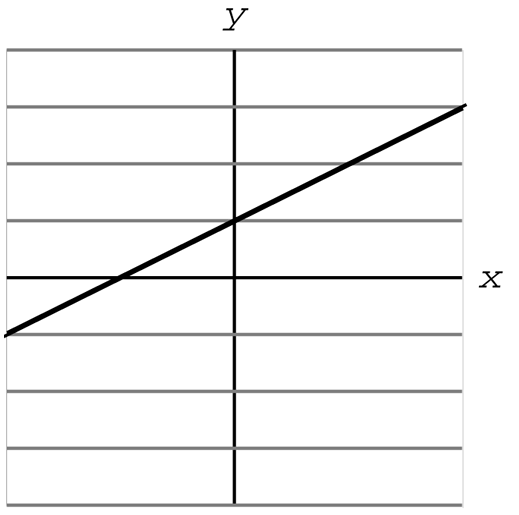
Una única solución cuando las dos líneas tienen distinta pendiente (se cruzan):

Un número infinito de soluciones cuando las dos líneas tienen la misma pendiente e intercepción-y (pasan por el mismo sitio):

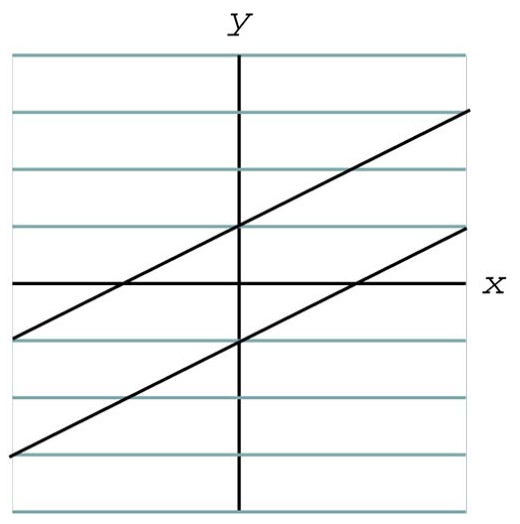
Ninguna solución cuando las líneas tienen la misma pendiente pero diferente intercepción-y (son paralelas):

Matemáticamente determinar las soluciones es tan sencillo como comparar las pendientes (m) de las dos ecuaciones lineales:

• Si m1 != m2, una solución (hay colisión):

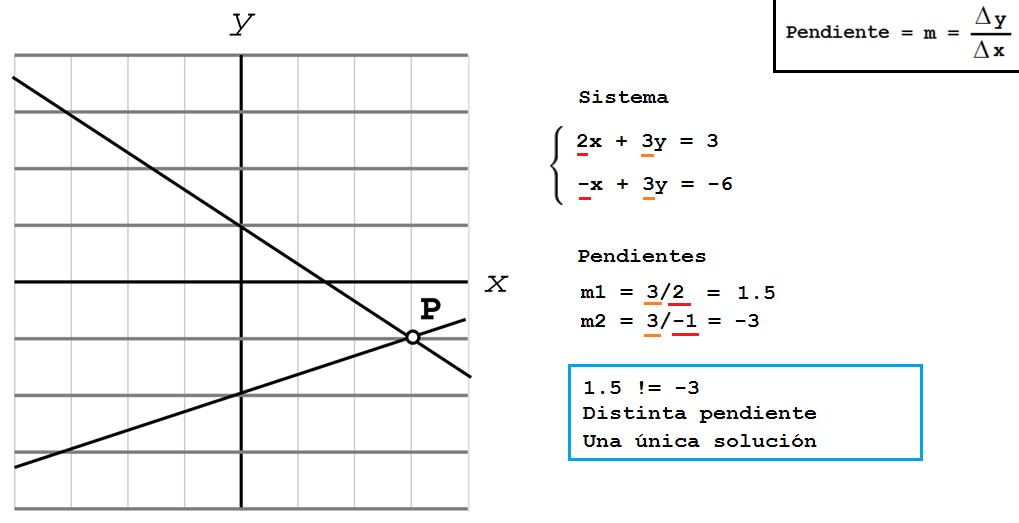
Cuando sabemos que sólo hay una solución podemos calcular exactamente el punto de intersección resolviendo los sistemas utilizando el método de la sustitución para dos incógnitas (o cualquier otro método):

• Si m1 == m2, buscar intercepción-y de las dos líneas, b1 y b2:

  • Si b1 != b2, cero soluciones (no hay colisión):
  
  • Si b1 == b2, infinitas soluciones (hay colisiones):