Líneas (Ecuaciones lineales)¶

¿Qué es una Línea?¶

Una línea, también llamada ecuación lineal es un tipo especial de función. ¿Recordáis que cuando definimos una función lo hicimos con pares ordenados de números o puntos?

Cada uno de estos puntos es una solución individual de la ecuación y = 2x. La solución completa de la ecuación, en tanto, no es otra cosa que todos los puntos que satisfacen la ecuación. Si representas los puntos en el sistema de coordenadas y trazas líneas entre ellos aparece un interesante patrón:

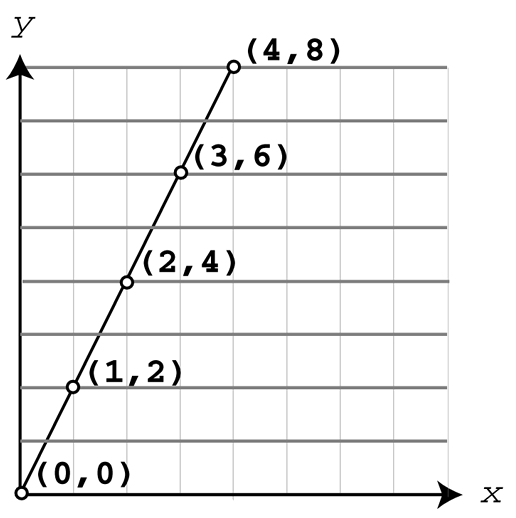
¿Lo veis claro ahora? Este patrón no es otra cosa que una línea, por éso se llama ecuación lineal. El gráfico de una ecuación de forma Ax + By = C, donde A y B no son ambas 0, es siempre una línea recta. Inversamente, toda línea recta tiene por ecuación la forma Ax + By = C cuando A y B no sean ambas 0.

La forma más simple de dibujar el gráfico de una ecuación lineal en el sistema de coordenadas es transformar la ecuación dejando la y a un lado para calcularla. Luego se toma un valor para x, se sustituye y se busca el nuevo valor de y. Dos pares ordenados de números son suficientes para determinar el gráfico de una ecuación lineal pero es mejor utilizar un tercer par. Mantener bajos los valores de x, empezando con el 0 te será útil.

Por último debes tener en cuenta que una ecuación como y = 3, aunque no lo parezca también es una línea. Si lo piensas verás que se puede interpretar como 0x + 1y = 3, es decir, no importa el valor de la x, la solución únicamente implica y = 3. Si tomas algunos valores para x para dibujarlos en el sistema, por ejemplo -1,0,1 verás qué ocurre:

Pues evidentemente, que no importa el valor de x, la línea siempre pasará por y = 3, trazando una línea horizontal perfecta. De hecho en una ecuación lineal siempre que x sea 0 tendremos una línea horizontal, mientras que si es la y la que vale 0 tendremos una línea vertical.

Propiedades de las líneas¶

Vamos a tomarnos un rato para analizar más a fondo las líneas. Una de sus propiedades más importantes es la pendiente o inclinación. En la siguiente figura vemos un ejemplo de una cuesta que se eleva a 50 metros y tiene una longitud horizontal de 100 metros:

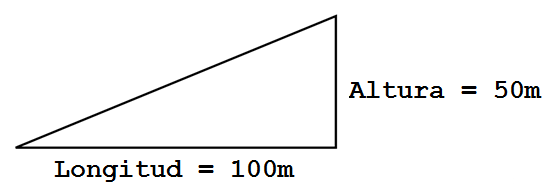
La inclinación de una pendiente se mide por la proporción entre la altura y la longitud, en este caso 50/100 (½), que sería un 50% de inclinación (½x = y). Pues esta misma cuesta se puede representar matemáticamente con una ecuación lineal: ½x - y = c:

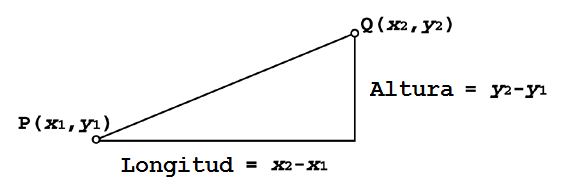
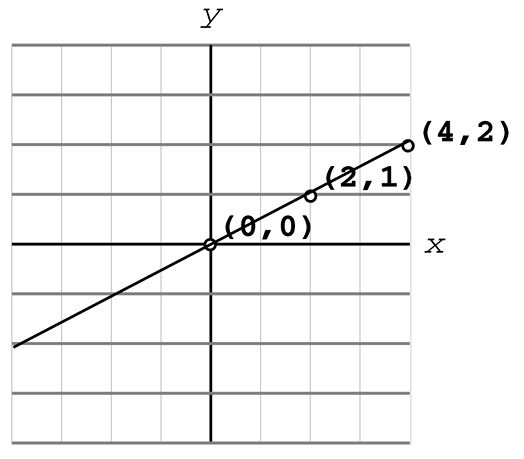
Fíjate en la coordenadas de los puntos P y Q. Como puedes observar, la línea se alza en una proporción de 1 unidad vertical por cada 2 unidades horizontales, lo que significa que la pendiente es ½. La notación general para la pendiente es la letra m, teniendo en cuenta los puntos P(x1,y1) y Q(x2,y2) la fórmula es:

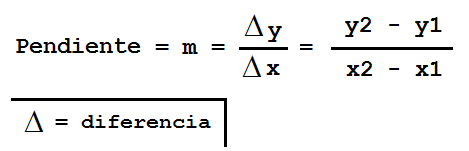
No importa qué puntos escojas, la proporción siempre será la misma para cualquier par de la misma línea. Por ejemplo en la siguiente figura, ya sean los puntos P y Q para calcular la pendiente: m = (2-1)/(4-2) = ½ . Si utilizas el punto P y el origen: m = (1-0)/(2-0) = ½ o el punto Q y el origen: m = (2-0)/(4/0) = ½, la pendiente es siempre ½: