Operaciones con vectores¶

En los gráficos por computadora, saber cómo determinar si las caras de un modelo se encuentran revertidas nos permitirá ahorrarnos su renderizado. Para conseguirlo deberemos aplicar algunas operaciones con vectores así que en esta sección vamos a repasar diferentes operaciones vectoriales.

Magnitud vectorial¶

La longitud de un vector v es lo que se conoce como su magnitud ||v||.

Podemos calcular la magnitud como la hipotenusa formada por los catetos v.x y v.y. Por tanto aplicando el teorema de Pitágoras:

Podemos añadir esta fórmula como un método de nuestros vectores:

float Vector2::Length()
{
    return sqrt(v.x * v.x + v.y * v.y);
}

float Vector3::Length()
{
    return sqrt(v.x * v.x + v.y * v.y + v.z * v.z);
}

Adición y sustracción de vectores¶

La adición es la suma entre dos vectores es el resultado de sumar los componentes de ambos vectores:

Podemos sobrecargar el método operator+ de nuestros vectores para realizar esta operación cómodamente. Es posible que tengamos que crear unos constructores antes:

Vector2() = default;
Vector2(double x, double y) : x(x), y(y){};

Vector2 Vector2::operator+(const Vector2 &v) const
{
    return Vector2(x + v.x, y + v.y);
}

Vector3() = default;
Vector3(double x, double y, double z) : x(x), y(y), z(z){};

Vector3 Vector3::operator+(const Vector3 &v) const
{
    return Vector3(x + v.x, y + v.y, z + v.z);
}

La sustracción es el proceso contrario, dado como resultado de restar los componentes de ambos vectores:

Podemos sobrecargar el método operator- de nuestros vectores para realizar esta operación cómodamente:

Vector2 Vector2::operator-(const Vector2 &v) const
{
    return Vector2(x - v.x, y - v.y);
}

Vector3 Vector3::operator-(const Vector3 &v) const
{
    return Vector3(x - v.x, y - v.y, z - v.z);
}

Multiplicación y división de vectores¶

La multiplicación y división a secas se toman como la idea de multiplicar o dividir tomando un factor. Esto resultará en un escalamiento del vector. Por ejemplo si el factor es 2 el vector resultante tendrá el doble o la mitad de longitud dependiendo de si se hace la multiplicación:

O la división:

Podemos sobrecargar los operadores de producto y división con un factor:

Vector2 Vector2::operator*(float factor) const
{
    return Vector2(x * factor, y * factor);
}

Vector2 Vector2::operator/(float factor) const
{
    return Vector2(x / factor, y / factor);
}

Vector3 Vector3::operator*(float factor) const
{
    return Vector3(x * factor, y * factor, z * factor);
}

Vector3 Vector3::operator/(float factor) const
{
    return Vector3(x / factor, y / factor, z / factor);
}

Producto vectorial¶

El producto vectorial (cross product) a×b es el vector perpendicular resultante de a y b, también llamado vector normal N.

Una manera de visualizarlo es como la dirección resultante del pulgar en la mano derecha tomando los dedos índice y corazón como dos vectores a y b:

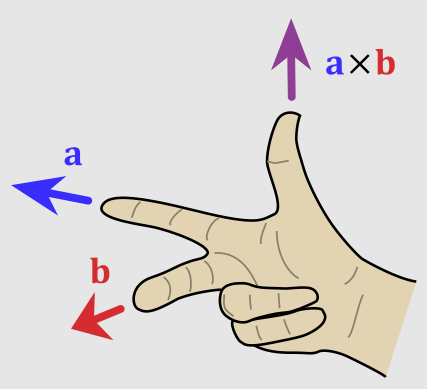
Para encontrar el resultado del producto vectorial (Nx, Ny, Nz) entre los vectores a y b aplicaremos la siguiente fórmula:

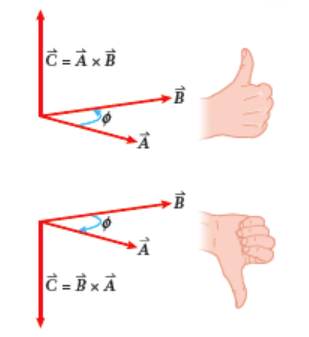
Debemos tener en cuenta que el resultado del producto vectorial no es el mismo si cambiamos el orden:

Esto tiene que ver con la dirección del sistema, pues si suponemos que la dirección es con sentido antihorario a x b, el vector normal resultante es perpendicular hacia arriba (se aleja), pero si es con sentido horario b x a es perpendicular hacia abajo (se acerca):

La siguiente figura muestra una animación del resultado del producto vectorial dependiendo de dos vectores:

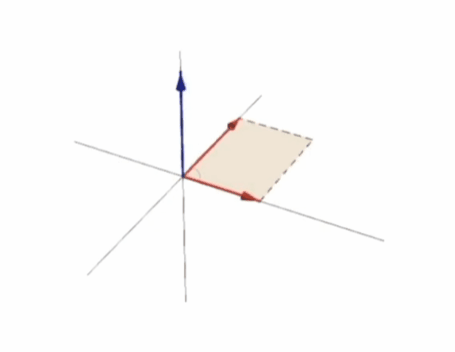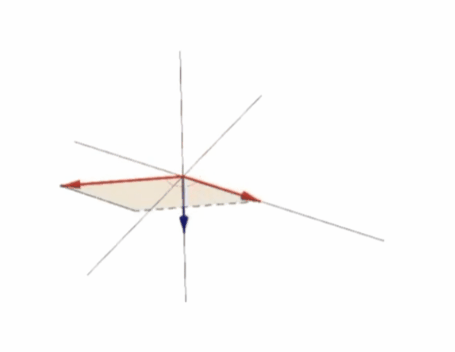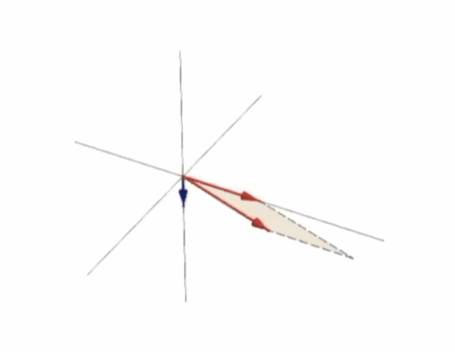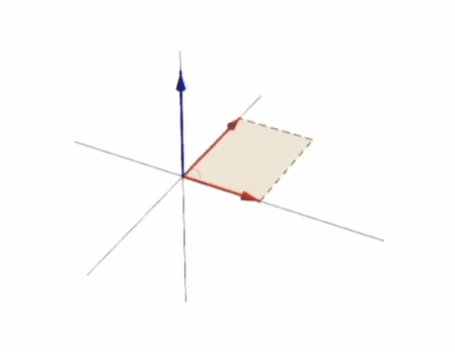
En ella podemos ver como al final todo tiene que ver con el área del paralelogramo formado por ambos vectores. Cuanto más alineados menor es el producto vectorial, cuanto más alineados mayor es y si están completamente alineados (son la misma línea) el producto vectorial es cero.

Vector normal de una cara¶

Así que pongamos en práctica lo aprendido para calcular el vector normal de una cara de nuestro modelo, la cuál nos permitirá saber hacia donde mira:

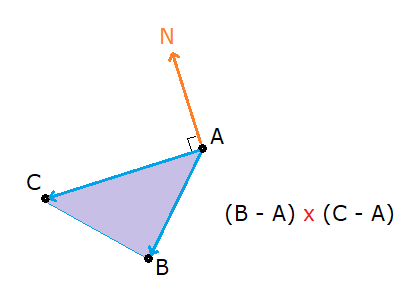
El producto vectorial entre dos vectores (B-A) y (C-A) da como resultado el vector perpendicular que forma un ángulo de 90º respecto a la cara del triángulo, pues es lo mismo que si trazamos el vector desde el centro de la cara:

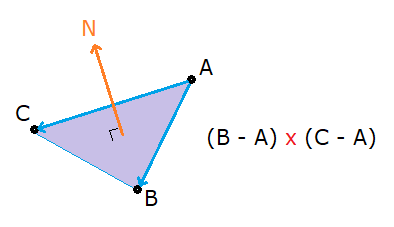
El método para calcular el producto vectorial quedaría de la siguiente forma:

Vector3 Vector3::CrossProduct(const Vector3 &v) const
{
    return Vector3(
        y * v.z - z * v.y,
        z * v.x - x * v.z,
        x * v.y - y * v.x);
}

Cabe mencionar que no hay algo así como un producto vectorial para dos dimensiones, en su lugar se utilizaría una operación matemática, pero como tampoco vamos a hacerla servir no lo voy a implementar.

Producto escalar¶

La última operación que nos resta ver es el producto escalar (dot product) a·b y su peculiaridad es que si bien el producto vectorial tenía como resultado un nuevo vector (llamado normal), el resultado del producto escalar tiene como resultado un único número llamado escalar.

Podemos visualizar este número como la proyección del vector b en a:

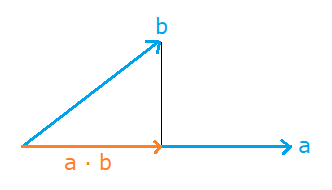
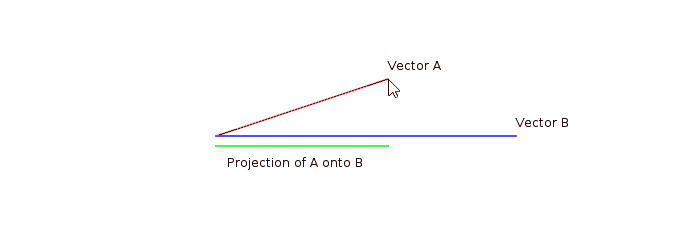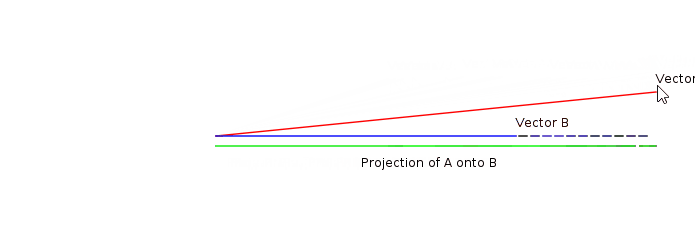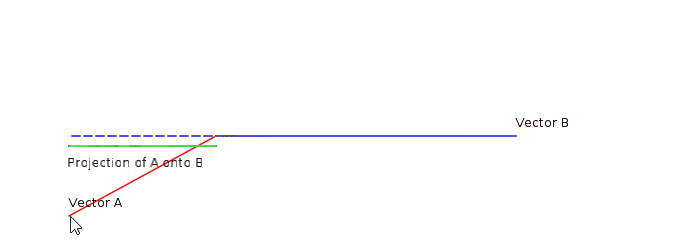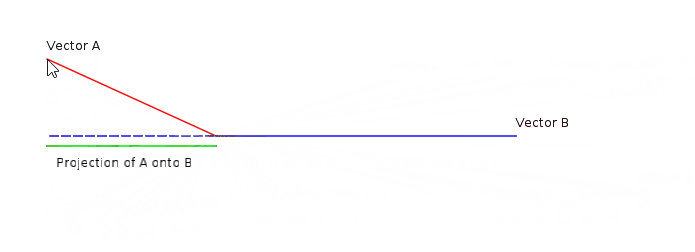
La siguiente animación muestra un ejemplo del producto escalar entre dos vectores:

Podemos enumerar algunas propiedades del producto escalar:

• Cuando los vectores se encuentran completamente alineados y tienen la misma longitud, el producto escalar es 1.
• Cuando los vectores forman un ángulo de 90º, el producto escalar es 0.
• Cuando los vectores son completamente opuestos y tienen la misma longitud, el producto escalar es -1.

La fórmula para calcular el producto escalar es:

Podemos crear el método en nuestros vectores sin mucha complicación:

float Vector2::DotProduct(const Vector2 &v) const
{
    return (x * v.x) + (y * v.y);
}

float Vector3::DotProduct(const Vector3 &v) const
{
    return (x * v.x) + (y * v.y) + (z * v.z);
}

Con esto ya lo tenemos y en resumen podemos quedarnos con la idea de que:

• El producto vectorial nos permite conocer el vector perpendicular entre dos vectores.
• El producto escalar nos permite conocer la alineación entre dos vectores.

Última edición: 05 de Junio de 2022